Yesterday, I had the pleasure of delivering a session with Craig Jeavons at #Mathsconf7 titled ‘Implementing Academic challenge in KS3 using Nuanced Problem Types’.
Craig and I joined forces because we teach in different parts of the country, in two different schools, but also because we work in contexts expressing the same philosophy and mindset about mathematics education. We both believe that teaching knowledge in year 7 and year 8 can be made more academically challenging by creating nuanced problem types, strengthening pupils’ understanding of a concept through designing a problem set using intelligent procedural variation. We both believe that memorisation of facts and creative thinking are not mutually exclusive.
Craig and I chose a topic each, in which to create different problem types: I chose indices whereas Craig chose fractions. We chose these two topics because we wanted to select topics that some may consider mundane and standard to teach, proving to our audience that challenges can nevertheless still be presented in the teaching of both topics.
In this blog post, I shall outline the six different ideas used in implementing a challenge in teaching the topic of indices.
- Basic factual recall
Indices, as a topic, relies on committing the knowledge of the first 15 square numbers and square roots, and the first 10 cube numbers, to memory. How can pupils commit this to memory? Ask them to try and recite it in the smallest amount of time possible? Give them a series of practice questions where they have to evaluate 93 (figure 1).

Figure 1 – Factual Recall exercise evaluating the first 15 square numbers and first 10 cube numbers.

Figure 2 – Facutal Recall exercise evaluating the first 15 square roots and first 10 cube roots
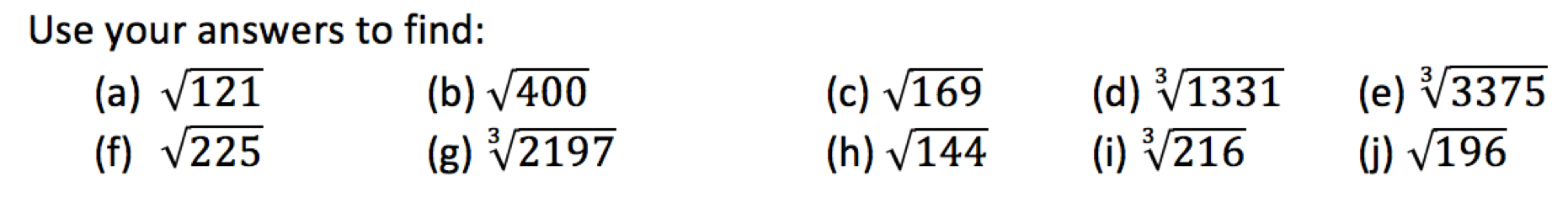
Figure 3 – Factual Recall exercise evaluating a mixture of square roots and including cube roots from 11 cubed onwards.
Give them a similar practice set of questions using square roots and cube roots (figure 2), and why not include questions where pupils have to evaluate calculations with square roots and cube roots (figure 3). Give them more than two terms in the calculation, include all four operations (figure 4). I like the second question, in particular, because pupils must distinguish the difference between √64 and ∛64 despite both looking visually similar (figure 5). This is deliberately designed to make them stop and think.
Figure 4 – Calculations with square and cube numbers
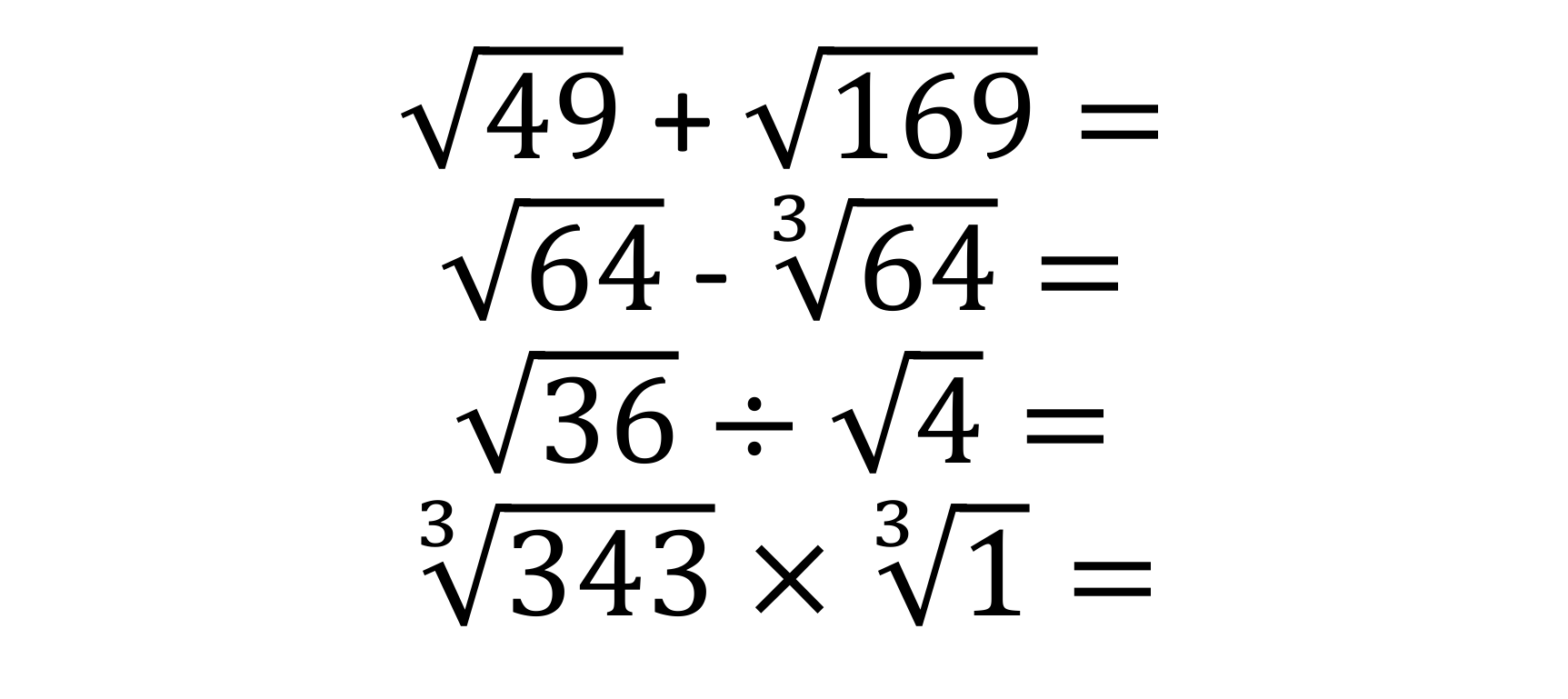
Figure 5 – Calculations with square and cube roots
I wanted my pupils to learn how to evaluate 113 because of the link between the powers of 11 and Pascal’s triangle (Figure 6). Each line of Pascal’s triangle relates to one of the powers of 11, so the first line of Pascal’s triangle is equivalent to 110, and so forth. My kids loved this so much! I would ask the following:
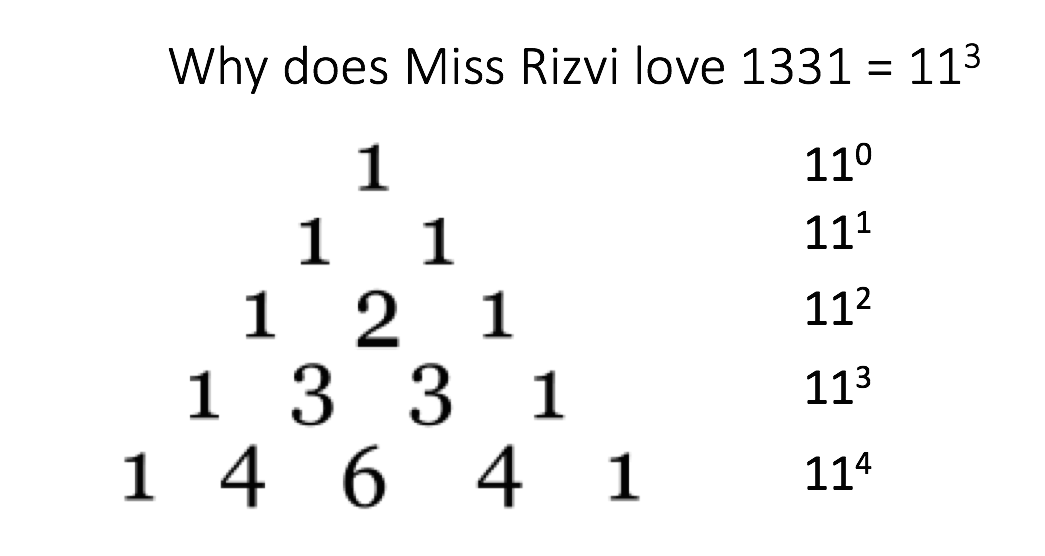
Figure 6 – Linking the the powers of 11 to Pascal’s triangle
Me: “What is my favourite cube number?”
Pupil: “113, Miss”
Me: Who can evaluate 113?”
Pupil: “1331, Miss,”
Me: “What is the name of the special triangle I mentioned last week, the triangle is not a shape but the numbers form a triangular structure?”
Pupil: “Pascal’s triangle, Miss”
Me: “What is the first line of Pascal’s triangle…What is the third line of Pascal’s triangle?”
Pupil: “1…121, Miss.”
Me: “How can I express 121 using Index form?’”
Pupil: “112, Miss.”
Me: “Now, what is the 6th line of Pascal’s triangle?”
Pupil: “15,101,051, Miss”
…so on and so forth. This type of questioning is reliant on pupils having memorised 110, 111, 112, 113 etc.
2.Pre-empting misconceptions
It is all well and good giving pupils the correct knowledge by using correct examples, but it is incredibly valuable giving pupils the non-examples too. Why? Pupils do incorrectly associate squaring with doubling; cubing with tripling; and square rooting with dividing, because 22 = 4 and √4 = 2. So, show them some non-examples too (figure 7 and 8):
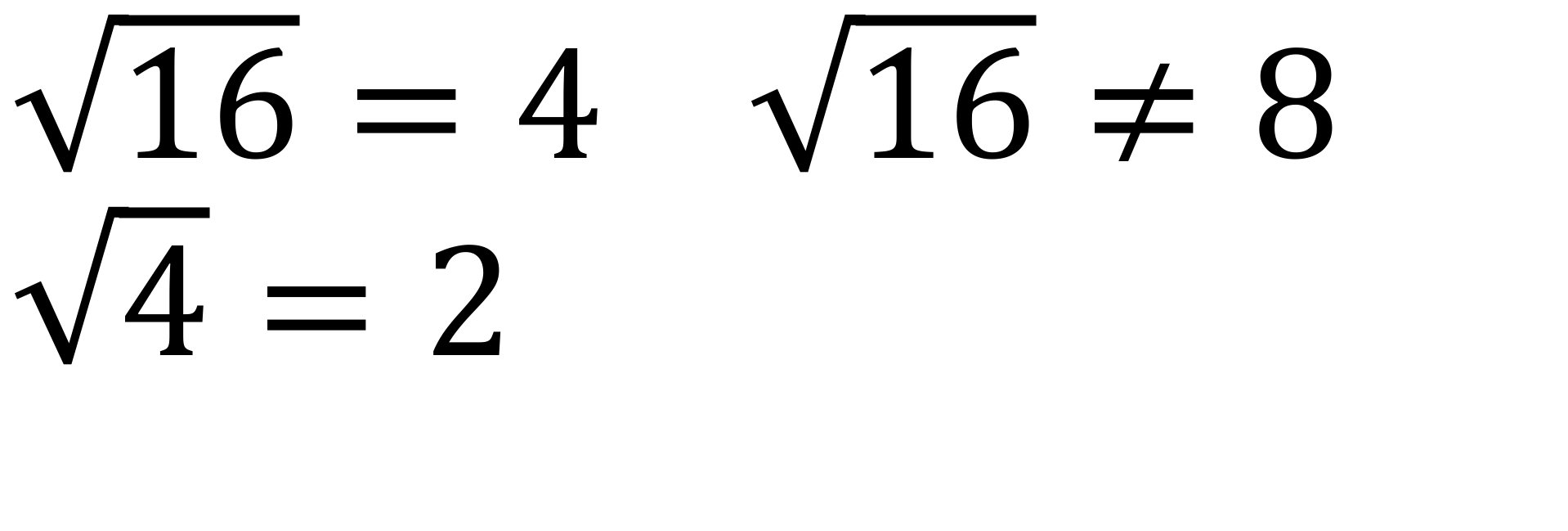 Figure 7 – Non examples of square and cube numbers
Figure 7 – Non examples of square and cube numbers
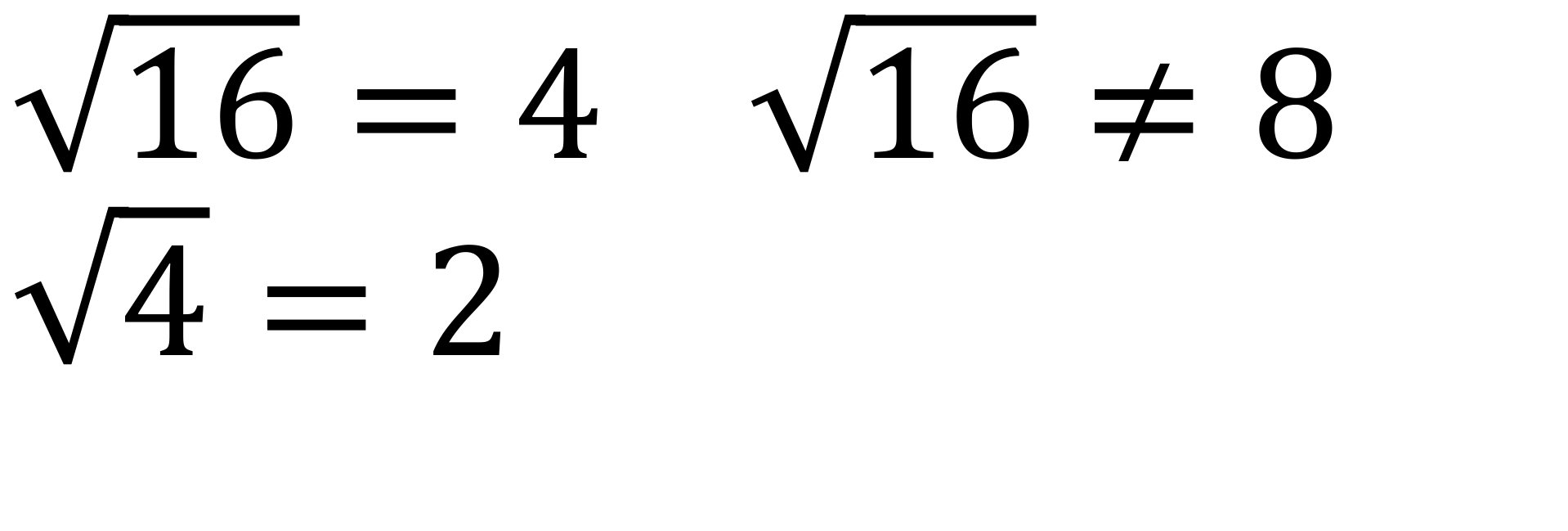
Figure 8 – Non examples of square roots
Have conversations around why visually similar problem types are not equivalent when evaluated (figure 9). Similarly, have conversations why visually similar problem types are equivalent when evaluated (figure 10). It does not matter the number of the root of 1, it will always equal 1.
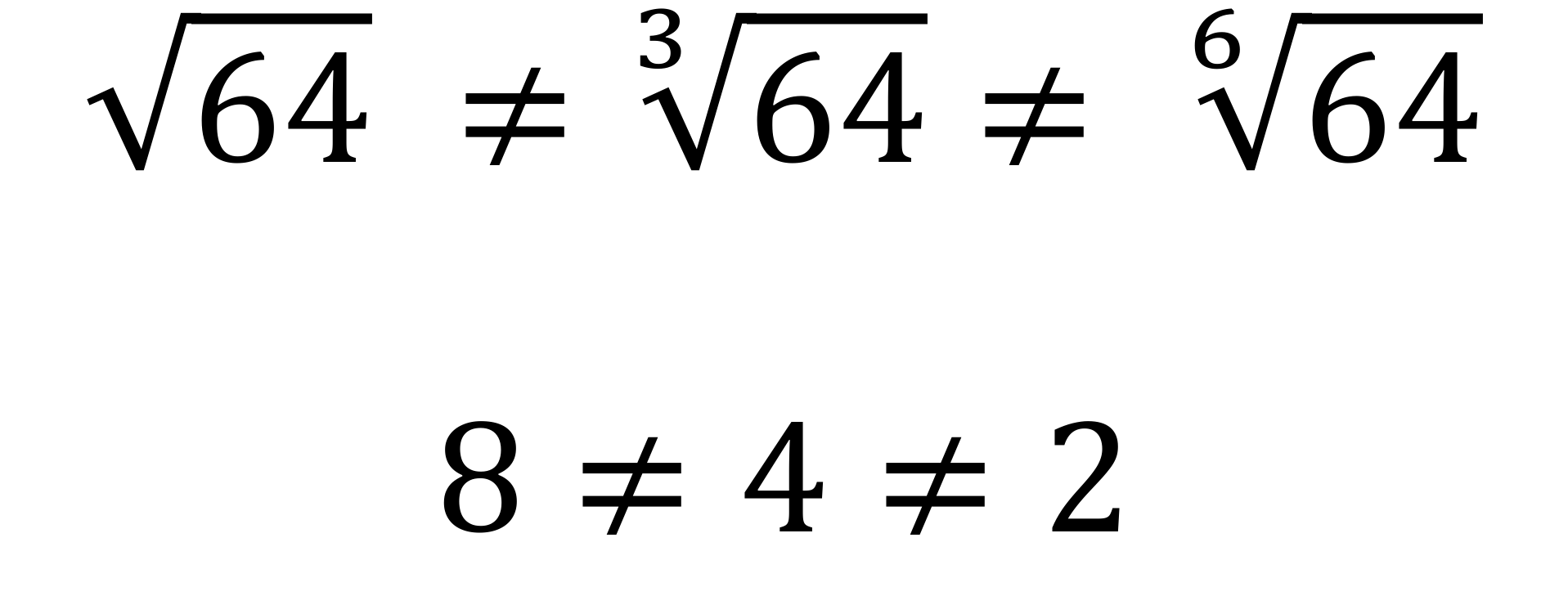
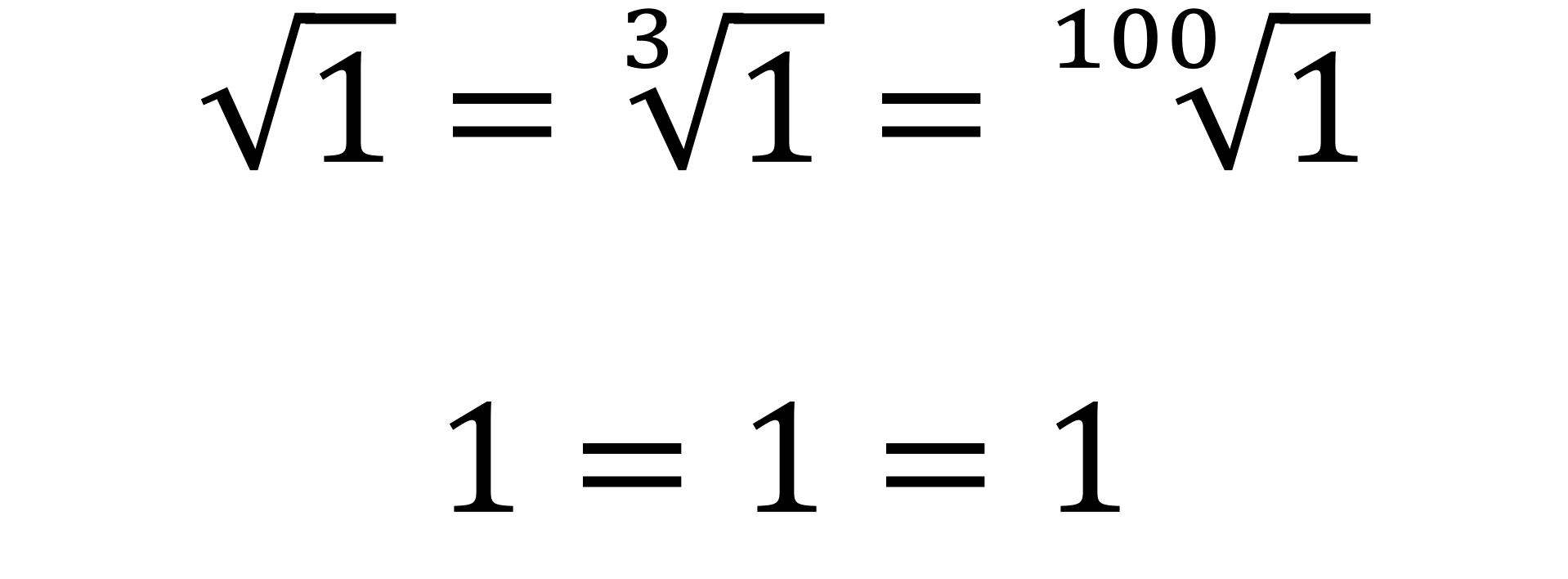
Figure 9 and 10 – Different problems which are visually similar
- Evaluating to the power of 0
This is an awesome piece of knowledge that the kids can learn and pick up. The best way for them to learn this is for them to identify that, regardless what the base value is, when evaluated to the power of 0 it shall equal 1. Include a base value where it is a one digit number, two digit and three digit example; make the base a decimal, variable and fraction. Craig later on mentioned that, when he was visiting schools in Shanghai, a teacher at one of the schools said “If you have taught it, then use it.” If pupils have learnt about decimals, fractions and variables, then show them that when you evaluate anything to the power of 0 the answer is 1. (figure 11)
Figure 11 – Evaluating to the power of 0 using any base value
This then allows you to make your initial practice set of questions incredibly challenging, by including complex examples such as evaluating to the power of 0, evaluating 1 to any index number, evaluating any base number to the power of 1 etc (figure 12) . You can then scatter these newly learnt problems with previously attempted problems; and you have varied the problem set where you expect pupils to still be thinking about each and every question (figure 13).

Figure 12 – Exceptional cases of Indices – because of their answers
I did add questions where the power was greater than 3, additionally, to add some more challenge to the practice set (figure 13).

Figure 13 – Practice set with intelligent varied problem types
- Multiple representations of square rooting and cube rooting
This relates to my first point in respect of basic factual recall. I will now always teach pupils the fact that cube rooting a cube number is the same as evaluating a cube number to the power of 1/3. Show them a different example, the fifth root of 32 is equivalent to evaluating 32 to the power of 1/5. They are seeing the pattern between the number of the root and the denominator of the fractional power. (figure 14)
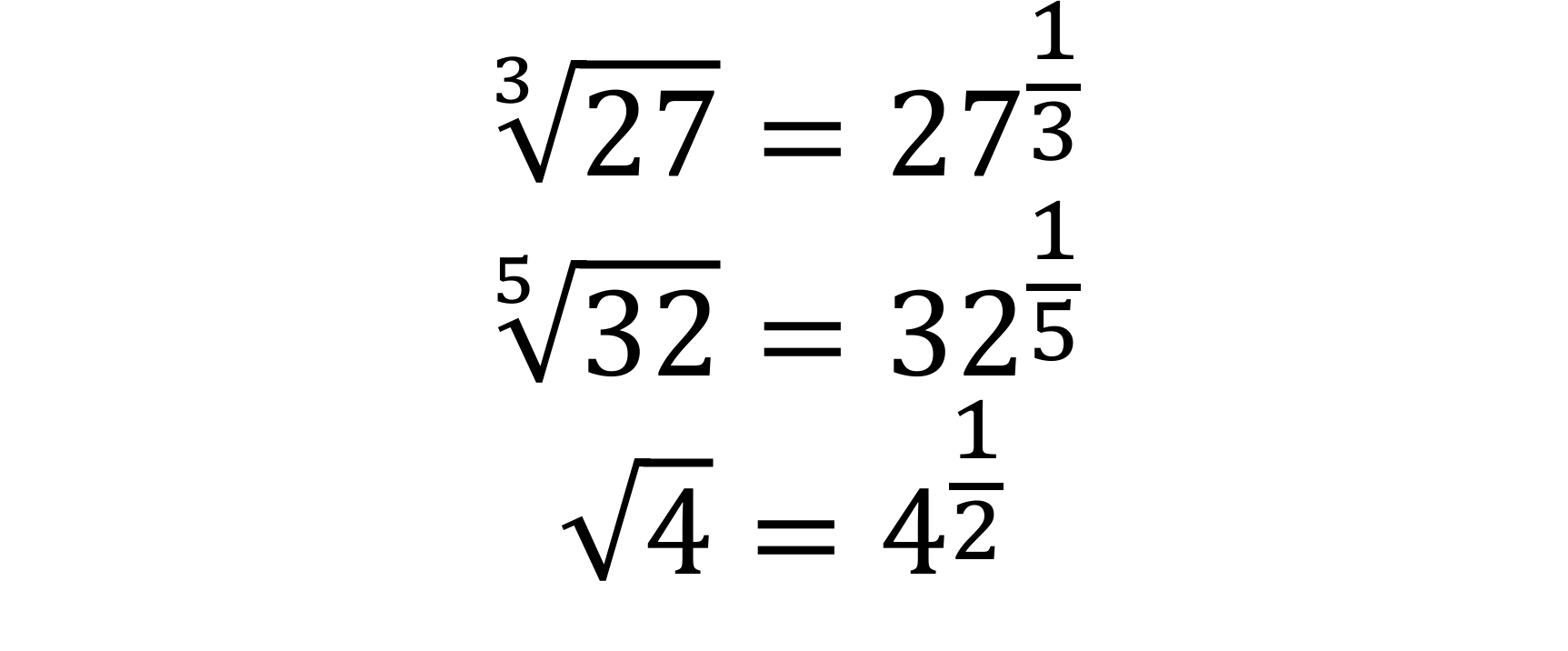
Figure 14 – Demonstrating the pattern between the number of the root and the denominator of the fractional power where the number being rooted is equivalent. Multiple representation of the same knowledge fact.
Why did I not start with the square root of a square number? The pattern is not obvious visually because the square root does not have the 2 visible like the third root of 27 or the fifth root of 32. Start with examples which state the pattern in an obvious and explicit manner, showing the exceptional examples at the end.
5.Complexity in structure rather than content
Now, if I return to the initial practice set of questions, which includes calculations with square roots and cube roots (figure 15), I can use essentially the same questions but only now using a different set of visual representations of the same problem (figure 16). I have just made the teaching of the concept more difficult by making the structure of the problem more complex. The content here is the same as the previous exercise when I showed calculations with square roots and cube roots. The content is also the same because it relies on the same factual knowledge I expected pupils to memorise in the initial stages of teaching the topic.
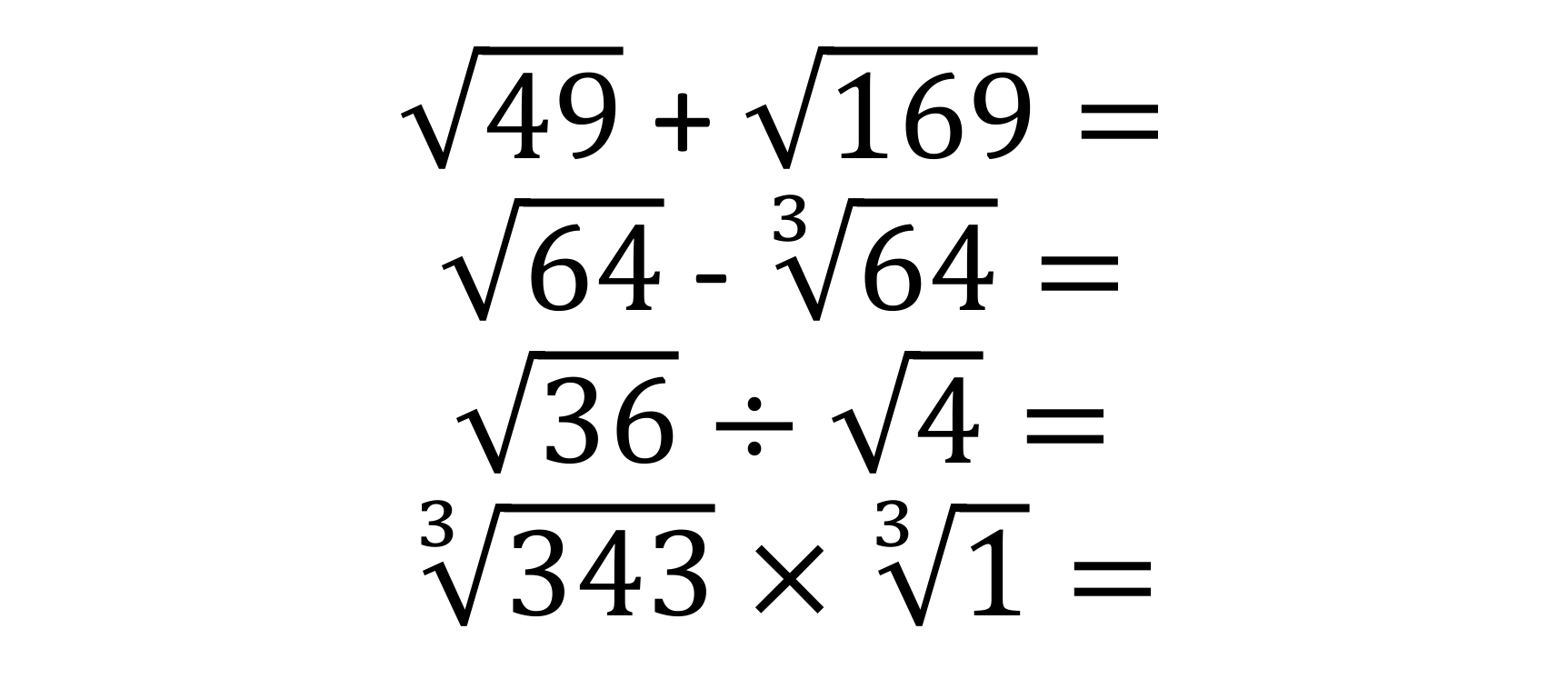
Figure 15 – Initial problems using square roots and cube roots in calculations
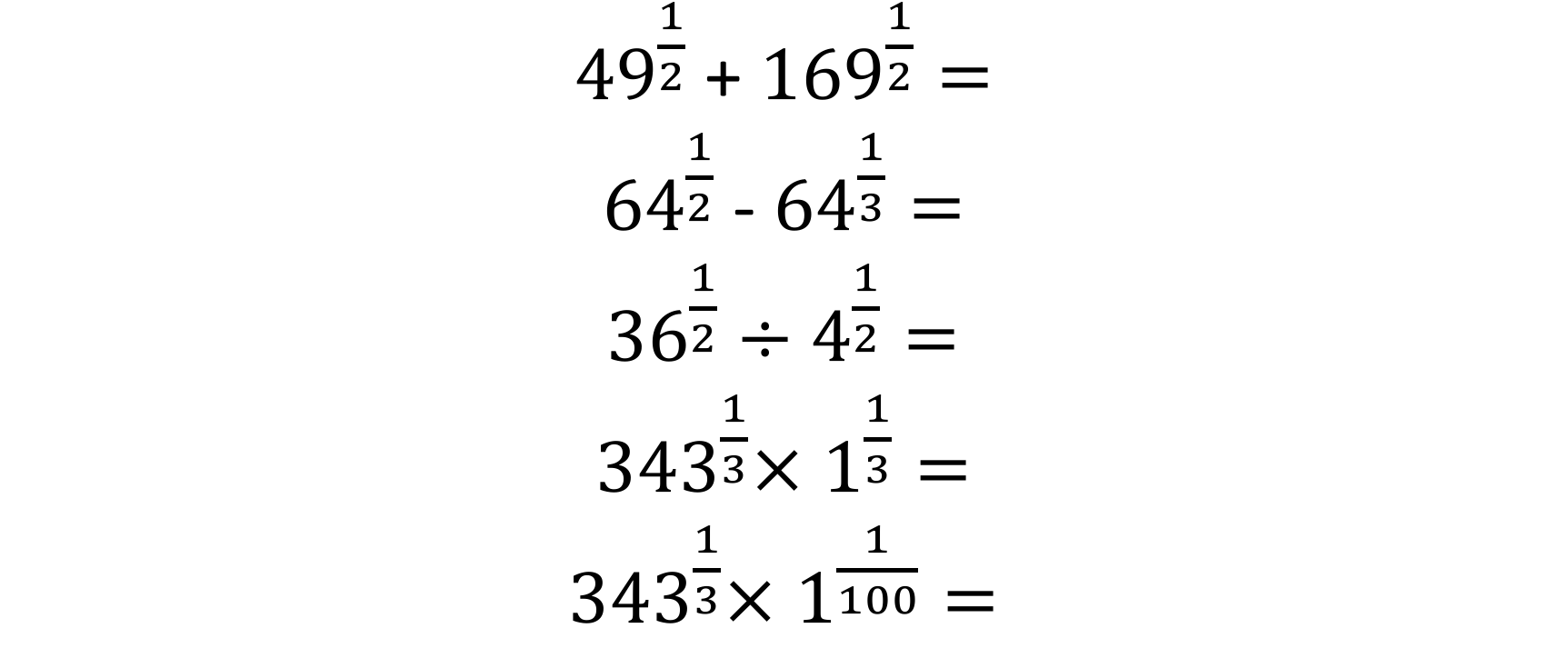
Figure 16 – Same problem types from figure 16 but using a different visual representation where square rooting of 49 is displayed as evaluating 49 to a power of 1/2.
Remember, in the previous image where I showed that any number to the root of 1 will result in an answer of 1. I can now present students with the last problem type where 1 has a power of 1/100 (last problem in figure 16). Each questions relies on the same factual knowledge but whereas this is displayed differently – visually – and this is challenge I am referring to because it is still difficult for students to identify the structure of the problem and make the link that 3431/3 is equal to 7 and that 11/100 is equal to 1. I love it!
6.Partial knowledge recall
We have asked pupils to attempt a full problem, such as ‘evaluate 53’, and to then determine its answer. Now, give them an incomplete problem with the answer given. Can they fill in the blanks? This is extremely difficult because they can no longer rely on their factual knowledge to determine the answer; they must instead manipulate such factual knowledge to complete the problem using the answer. Can they identify the missing index number? Can they identify the missing base number? (figure 17)
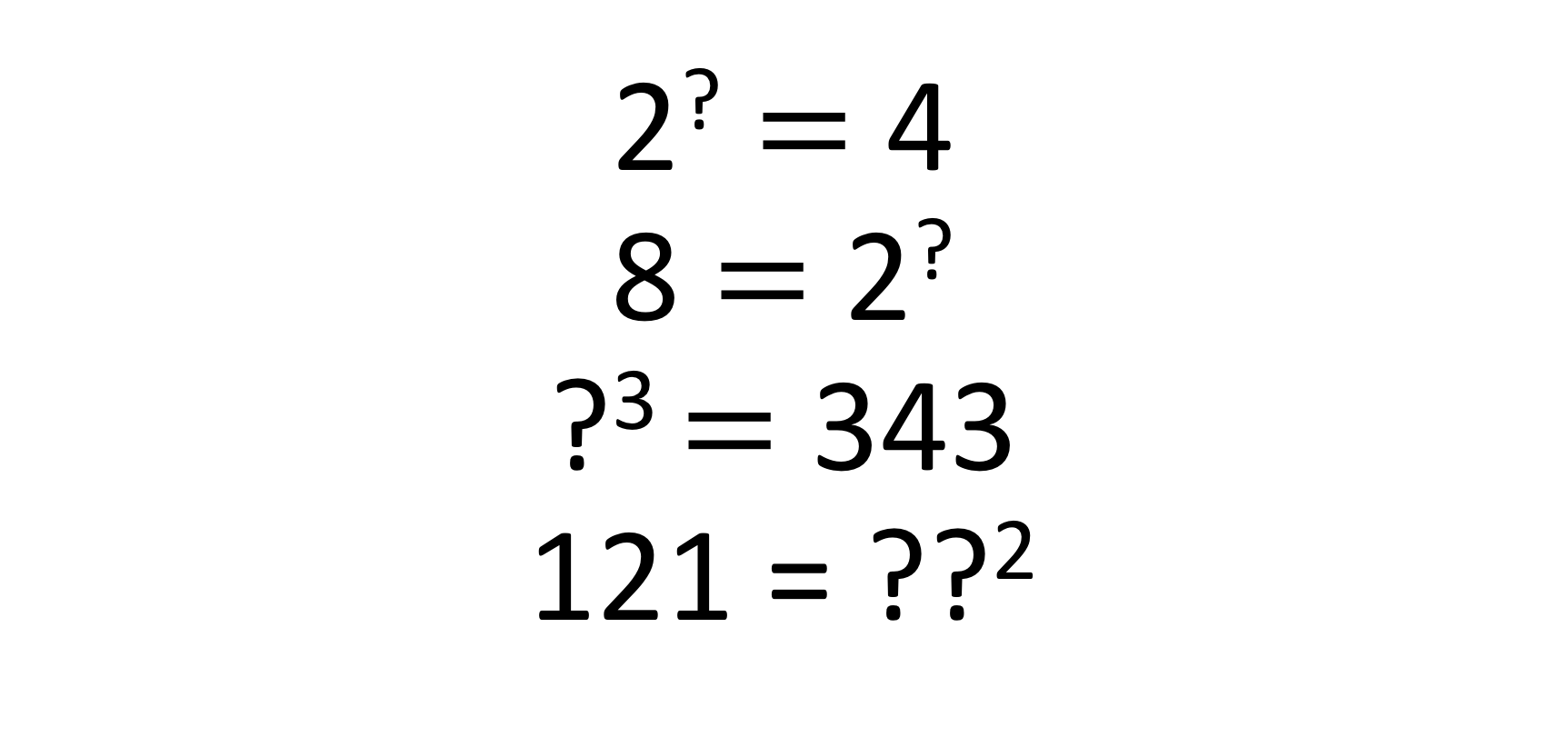 Figure 17 – Problem types requesting partial knowledge factual recall
Figure 17 – Problem types requesting partial knowledge factual recall
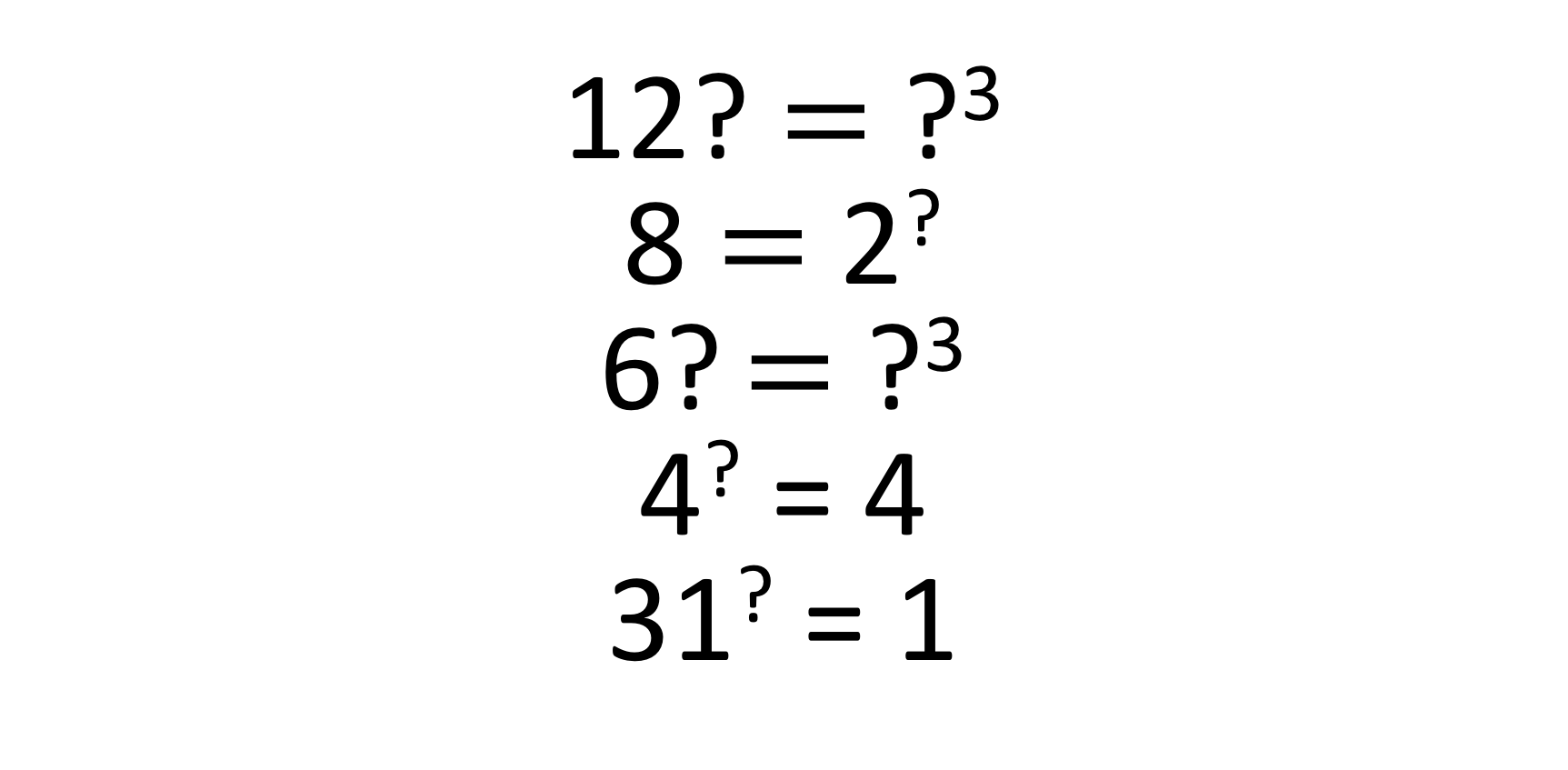 Figure 18 – Problem types where more than one part of the problem or answer is missing.
Figure 18 – Problem types where more than one part of the problem or answer is missing.
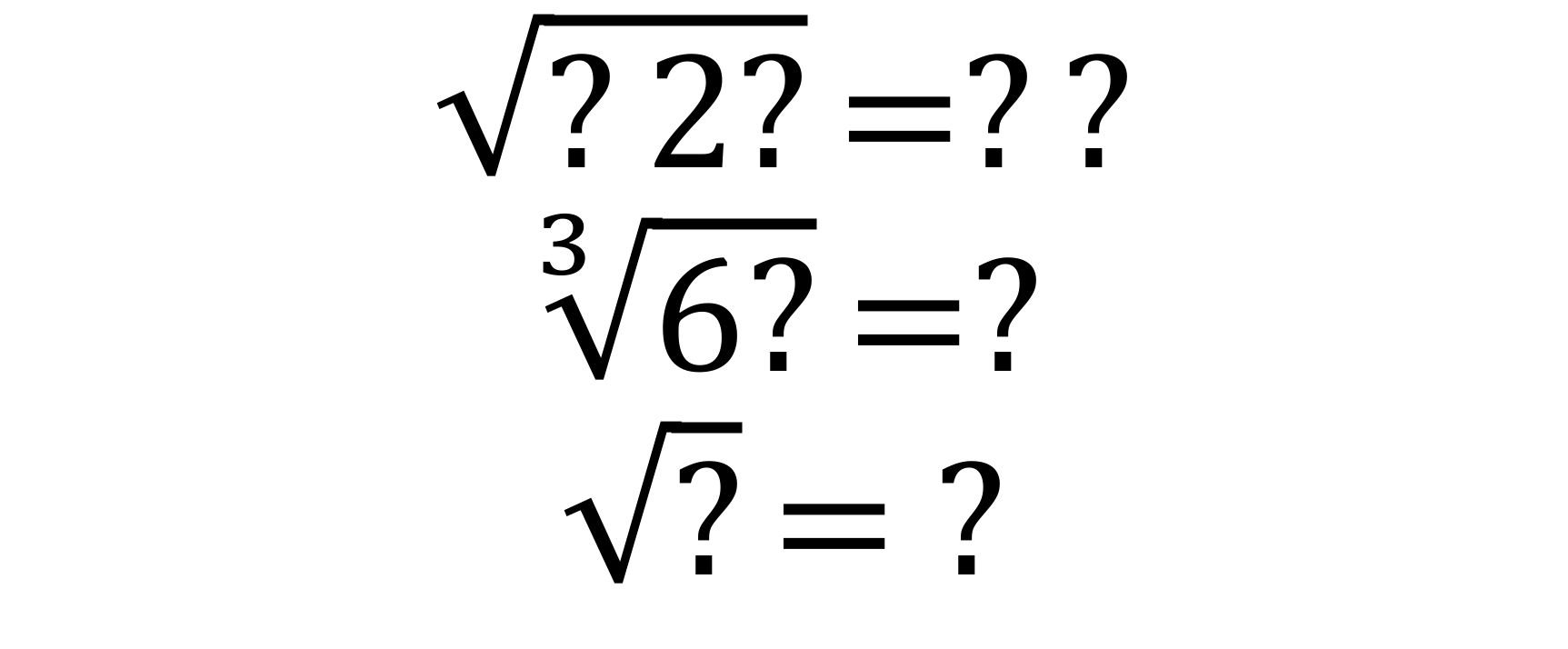
Figure 19 – Problem types requesting partial knowledge factual recall using square and cube roots.
Can they identify the missing base number and index number in the same problem? What about the fourth problem type? Even better, what about the last problem type? (last two problems in figure 18)
Pupils will be thinking, what power can I evaluate 31 with which gets me an answer smaller than the actual base number? 0! How do pupils know this? They know the fact that if you evaluate any base value to the power of 0 we always get 1. Let’s include examples with missing digits in the square root? Here the question marks represent the same digit. What about the last example – the only possibility is that both the question marks are 1. (figure 19)
Give them a practice set of questions where they have to attempt filling in the blanks in not only the problem but in the answer too. (figure 20)
Figure 20 – Partial knowledge recall exercise.
And so, that was a whistle stop tour on how teaching the topic of indices can be made more challenging, and in particular in respect of year 7 and year 8 classes, as presented at #mathsconf7. These six different ideas allow children to consolidate their knowledge of different facts about square numbers, cube numbers, square roots and cube numbers, through the six different ideas discussed above.
I have attached a PDF of the powerpoint presented at La Salle via a link below.
https://www.dropbox.com/s/l73m3sc87nuos77/PresentationLaSalle%23mathsconf7%20Naveen%20and%20Craig%20.pdf?dl=0]
If there are any questions then please do not hesitate to get in contact with either Craig or myself via Twitter (@naveenfrizvi and @craigos87) or via email (naveenfrizvi@hotmail.co.uk). Enjoy!
Thank you to everybody who took the time out of their weekend to attend mine and Craig’s workshop; we really appreciate your time and enthusiasm. Thank you to La Salle who hosted another great conference – you guys are awesome!
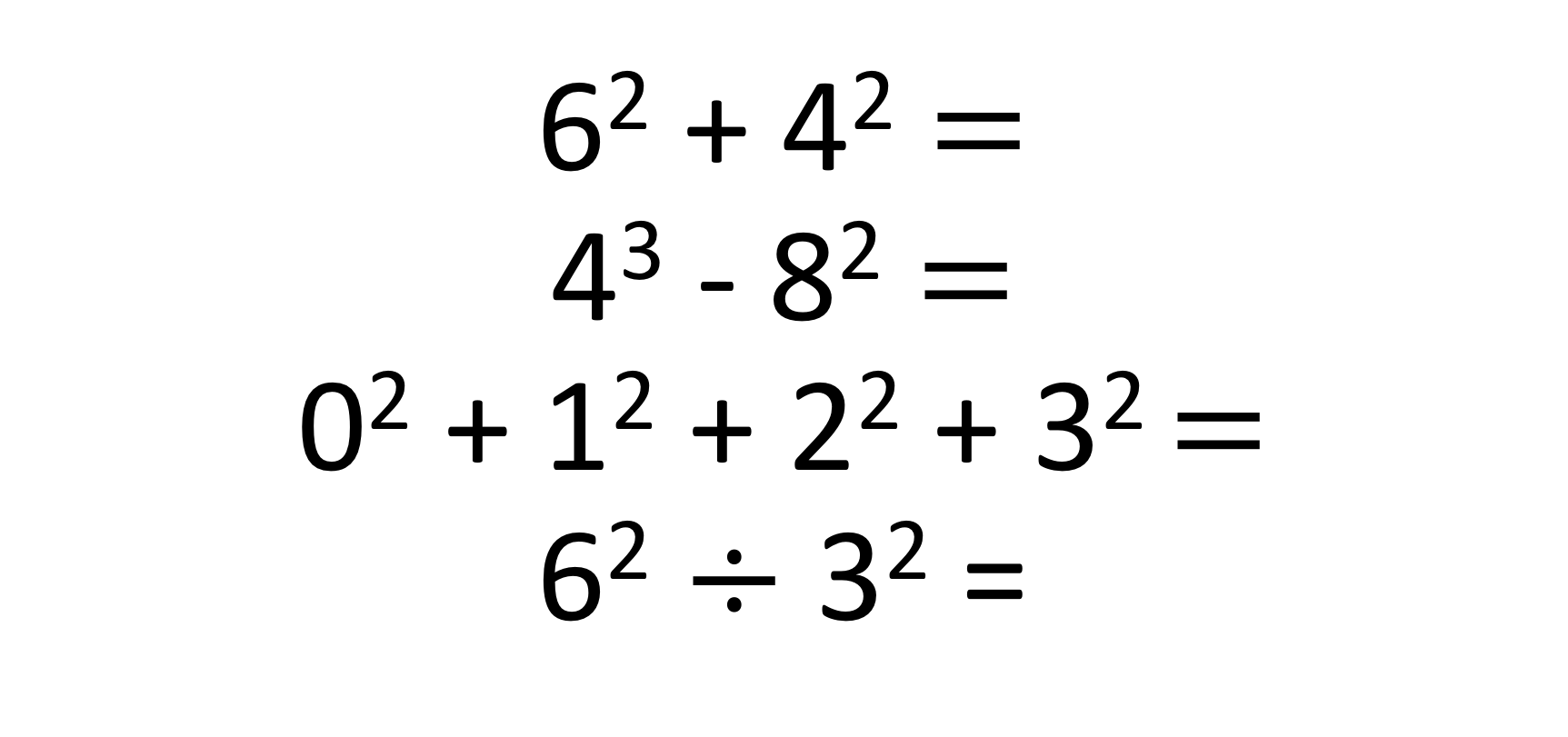
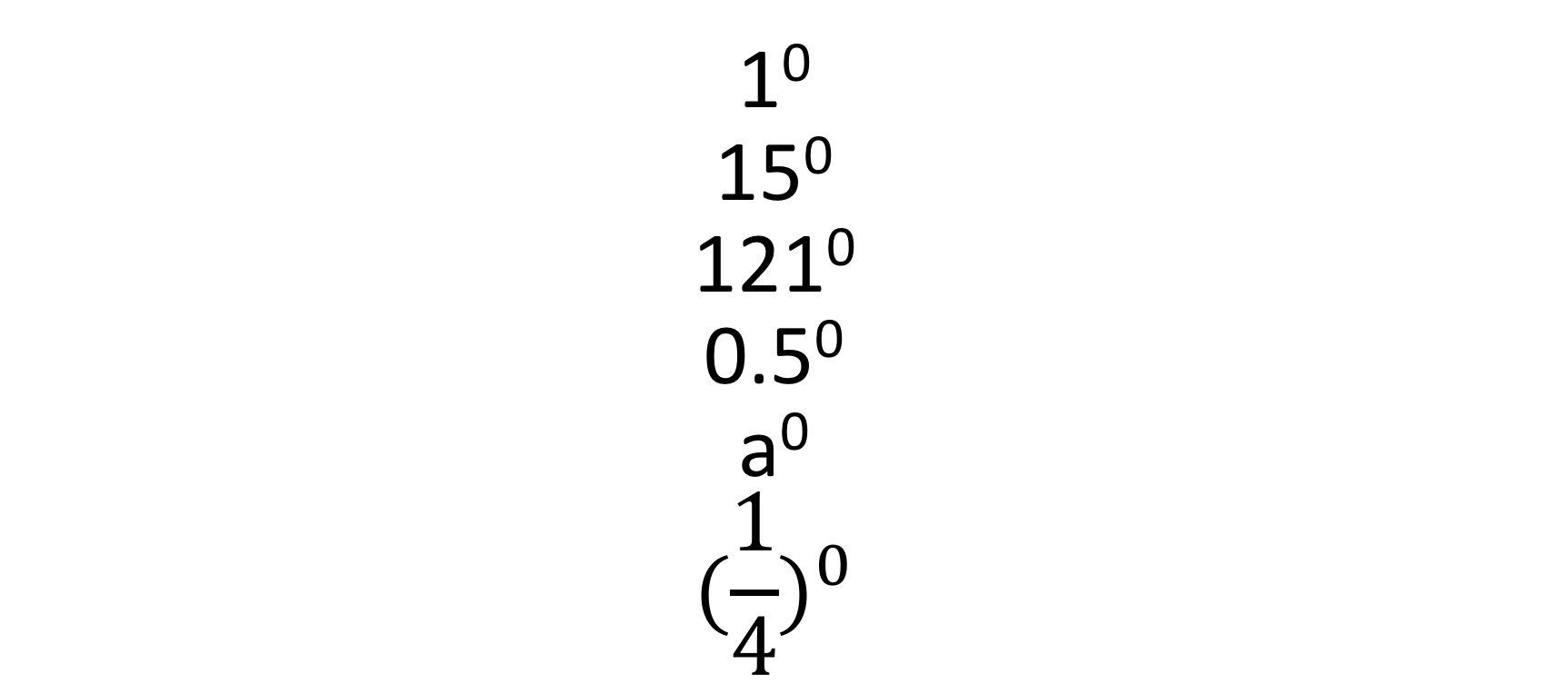
Recent Comments