This blog post is a follow up of the ‘Reattempting Circle Theorems’ blog post series. Last time we looked at this circle theorem:
Circle Theorem #1: A right angle triangle in a semi-circle
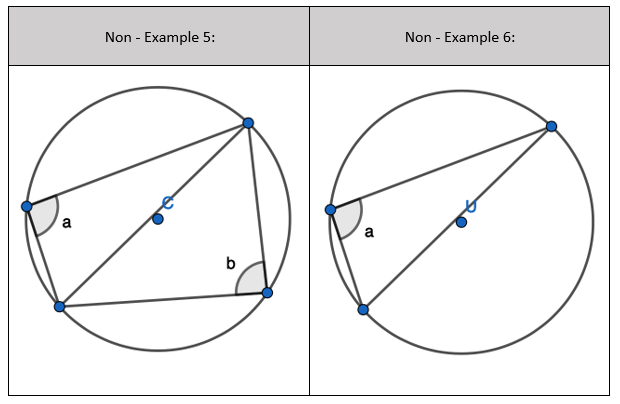
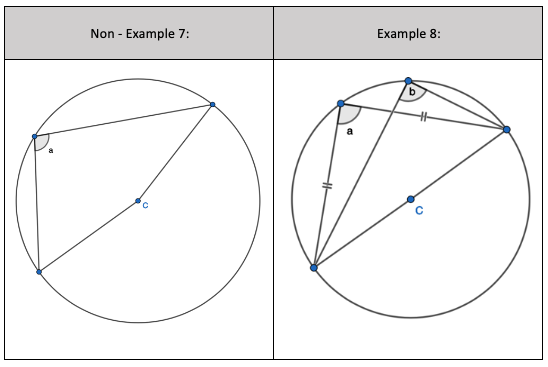
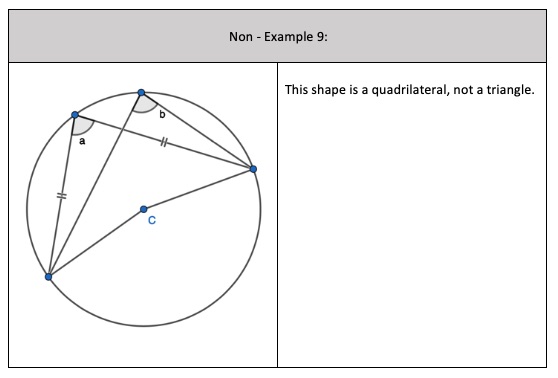
We will now look at a potential non-circle theorem. I’m opening this up for debate. I’ve had a look around online and in articles whether ‘Two radii and a chord form an Isosceles triangle’ is considered a circle theorem or not. Right now, I’m going to state it is not a circle theorem but instead the start of a proof about the perpendicular bisector of a chord. Thank you to Ed Southall for clarifying. Follow him – he’s my geometry go to! I am flexible to change my mind.
I deliberately included this after the first circle theorem so I could interleave it into new problems.
If I have a triangle where two lengths are radii and the third length is a chord, then it will be an Isosceles triangle. Two radii connected by straight line at both endpoints form an Isosceles triangle. The two of the side lengths are of equal measure.
I hope all pupils will be able to access a mathematical problem like this:
Show that: Two radii and a chord form an Isosceles Triangle
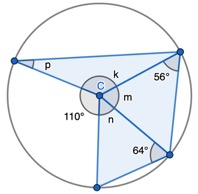
Here is a diagram for you to see this circle theorem form:
I have a circle where I draw one radius:
I draw another radius:
I draw a straight line between the two endpoints of each radii which are on the circumference of the circle:
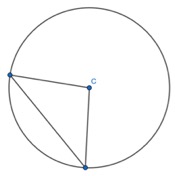
I then would show pupils that I can mark the two radii to show they are of equal length. I would show that the two equal angles of the triangle are of same size. And even mark the angles with identical values. I would do this live rather than with static images:
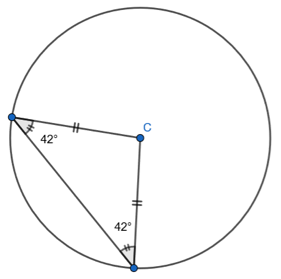
Now, there are two types of angles you can find:
1) One of the two equal angles
2) One non-equal angle
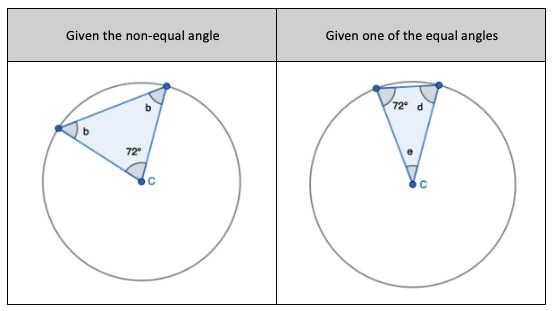
To find one of the equal angles, you’ll have the non-equal angle. Here are the steps:
- 180 degrees – non-equal angle
- Divide the result by 2
To find the non-equal angle, you’ll have one of the equal angles. Here are the steps:
- Double one of the equal angles
- 180 degrees – (double one of the equal angles) = Non-equal angle
The structure of the booklet is the same as outlined in the previous blog post. There are ‘I do, We do’ examples and then a practice exercise at the end. Since this isn’t a circle theorem, I’m not going to show a selection of examples and non-examples. But, I’m interleaving the first circle theorem into the sequence.
Finding the missing angle
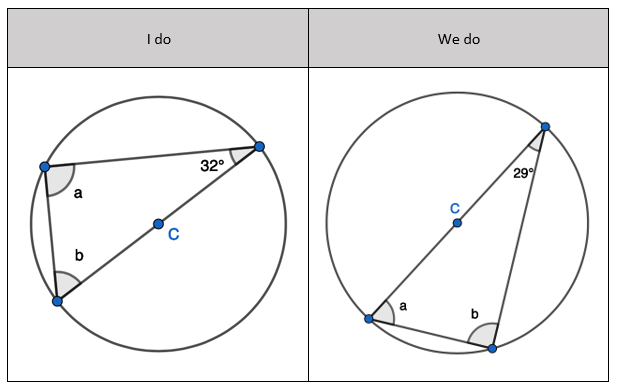
Here are the teacher examples to find a missing angle or angles. The variation between the examples isn’t evident here. I try to change one thing at a time between the ‘I do’ and the ‘we do’ example. I’ll explain the thinking behind choosing each example:
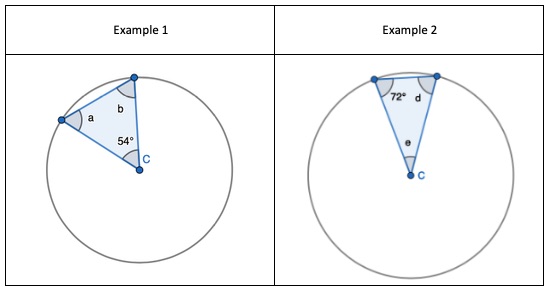 1. Show that two radii and a chord form an Isosceles triangle, only. Given the non-equal angle, find the one of the two equal sized angles.
1. Show that two radii and a chord form an Isosceles triangle, only. Given the non-equal angle, find the one of the two equal sized angles.
2. Show that two radii and a chord form an Isosceles triangle, only. Given one of the equal sized angles, find the missing non-equal angle.
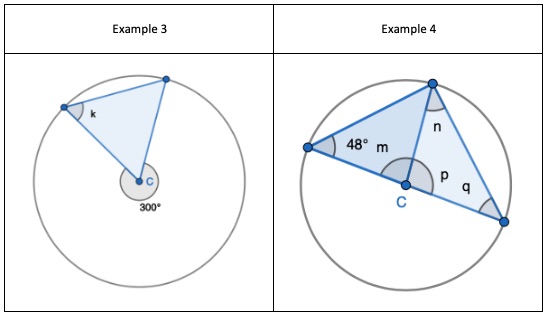
3. Interleaving the angle fact: angles around a point sum to 360 degrees. Find the non-equal angle to then find one of the two equal sized angles.
4. Two Isosceles triangles sharing a length. One triangle you are given one of the two equal sized angles to find the non-equal angle. Once you’ve calculated ‘m’ you can use the basic angle fact that angles on a straight-line sum to 180o to find ‘p’.
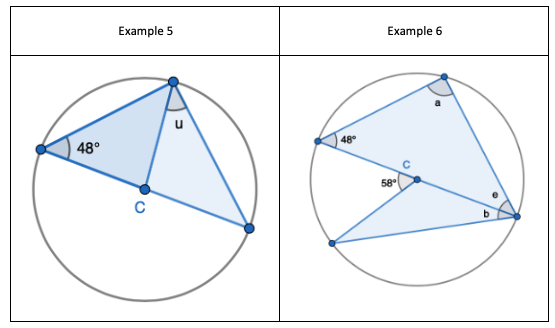
5. Same as Example 4 – angles needed to find before ‘u’ are not marked. Same logical steps. Also, can use the fact that angles on a straight-line sum to 180 degrees to then find ‘u’.
6. Interleaving the first circle theorem – A right angle triangle in a semi-circle
- Identify ‘a’ as a right angle of 90 degrees.
- Find ‘e’ by adding 48 and 90 degrees and then subtracting from 180 degrees.
- Find ‘b’ by finding the non-equal angle of the triangle using 180 – 58 degrees, and dividing the result by 2
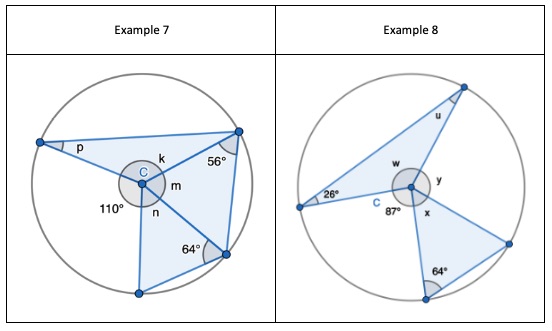
7. Three Isosceles triangles.
- Find ‘m’ and ‘n’ by doubling one of the two equal sized angles of each triangle and subtracting from 180 degrees.
- Find ‘k’ by using the fact that angles around a point sum to 360 degrees.
- Use ‘k’ to find angle ‘p’ by subtracting the non-equal angle and dividing the result by 2.
8. Two Isosceles triangles that are not sharing a side length:
- Find ‘u’ using the one of the two equal angles of the triangle
- Find ‘w’ by doubling the triangle’s two equal angles and subtracting from 180 degrees.
- Find ‘x’ by doubling 64 degrees and subtracting from 180 degrees.
- Find ‘y’ by using the angle fact that angles around a point sum to 360 degrees.
Algebraic Application
Another reason why I wanted to include this feature because it allows pupils to apply prior knowledge from the topic of solving equations. There are two problem types that we will have to deal with:
- Two equal angles labelled – solve equations with unknowns on both sides
In this case, the variable used for the two equal angles represented as expression will be the same. It has to so we can form an equation with unknowns on both sides to find the value of the unknown. I then labelled the non-equal angle with a different variable. I did this because I didn’t want to make an error in choosing an algebraic expression which shared the same variable as the two equal sized angles.
- All angles are an algebraic term, expression (same variable, not different) or number. Form equation and equate to 180 degrees
In the next problem type, I deliberately labelled the two equal sized angles with the same algebraic term or expression. This re-iterated that the two angles of the Isosceles triangle are equal. Given more time I would create more examples where the equal sized angles are labelled with different expressions sharing the same variable.
Is it possible for a mathematical problem be incorrect?
Thankfully, Tom Francome highlighted that I mislabelled one angle in a triangle with a different variable so the possibilities for that variable were endless:
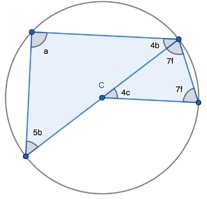
I changed ‘4c’ to ‘4f’ so that all angles in this triangle share the same variable. We can then collect the algebraic terms and equate to 180o to find the value of the unknown. We can substitute the value of the unknown back into the algebraic term to find the size of each angle.
Booklet attached:
https://drive.google.com/open?id=1rJmM29WeIXfOTCAE-rBdcXAM36S_SLFL
Recent Comments