At Michaela Community School we run a selection of extra curricular activities after school which complement pupils’ mainstream learning. In the Maths Department, we have a club called Mathletes. This club entails an additional hour of learning taking place once a week after school and it is specifically for one class that I teach (Top Set Y8).
This week I taught a session on imaginary numbers whereby pupils were able to solve the following equations independently:
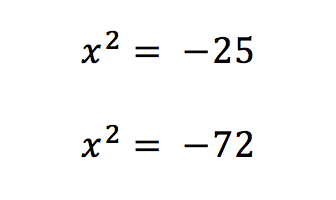 This blog is split into two parts. The first post will explain how I developed the pre-requisite knowledge pupils need to solve the equations above, with much focus placed on rational numbers because of the second equation. The second post will outline how I introduced a limited understanding of imaginary numbers, enabling pupils to solve both equations.
This blog is split into two parts. The first post will explain how I developed the pre-requisite knowledge pupils need to solve the equations above, with much focus placed on rational numbers because of the second equation. The second post will outline how I introduced a limited understanding of imaginary numbers, enabling pupils to solve both equations.
During my planning, I think of the pre-requisite knowledge pupils need in order to access the new topic that I will teach in the upcoming session. Before I started introducing the idea of imaginary numbers, I introduced the idea of rational numbers in a very limited sense. This was done deliberately – something which I will explain later on in this post.
A rational number is the square root of a square number which results in an integer answer. I introduced the concept like this.
This is not a rational number √2
This is not a rational number √3
This is a rational number √4
This is not a rational number √5
This is not a rational number √6
This is not a rational number √7
This is not a rational number √8
This is a rational number √9
This is not a rational number √10
This is not a rational number √11
This is not a rational number √12
This is not a rational number √13
This is not a rational number √14
This is not a rational number √15
This is a rational number √16
The above methodology was inspired by Kris Boulton’s talk on “The genius of Siegfried Engelmann”, delivered at The Maths and Science ResearchED conference in Oxford, and the National Mathematics Conference 7 in Leeds.
I asked pupils to raise their hands when they noticed the pattern. This was my introduction, because I wanted pupils to recognise that we can categorise the square root of a square number where the result is an integer as a rational number. I told them, for now, that this is a fact that you are going to accept and adopt, and that this is ok.
I am the classroom teacher of the pupils that attend the session and so I know how quick they are in recalling their square numbers and square roots. I also know they have memorised their times table facts from doing Bruno’s Times Table Rockstar programme, as rolled out in year 7 successfully by Bodil Isaksen, Head of Maths.
My next step was to pose the following question: “Now, we can spot which numbers are rational numbers, and which are not rational numbers. We are going to look at how we can rewrite the following in the form k where k is the largest possible integer, and √a is not a rational number.”
This is how it was laid out: “We are going to look at the number inside the square root. We are going to split it into two numbers each square rooted, where I have one square number, and one number which is not a square number.”
√72 = √36 x √2
“I am going to identify my square number which I can evaluate to get an integer.”
√72 = 6 x √2
“And I am going to rewrite it like this because we can”:
√72 = 6 x √2 = 6√2
Here k is 6 and √a is √2.
I also reiterated that I deliberately chose the largest square number (HCF) that can divide 72 because it is more efficient. I left it there, because I didn’t want to go into more discussion which would deviate pupils’ attention away from what I had shown on the board.
I then asked the pupils the following questions, before I asked them to simplify a selection of surds. I didn’t use the word surd because my focus for the session was not “what is a surd” or “how do I simplify surds” but because the point of this task was to develop sufficient pre-requisite knowledge in order to understand how we were planning to solve problems such as x2 = -72. This is why I previously mentioned that I introduced the idea of rational numbers in a limited sense.
Before pupils committed pen to paper to simplify the following surds I asked these questions which pupils answered by raising their hands.
“How can I rewrite √98 as a calculation where I am multiplying a rational number and a non-rational number, the rational number is a square number being square rooted?”
√98 = √49 x √2
“How can I rewrite √242 as a calculation where I am multiplying a rational number and a non-rational number, the rational number is a square number being square rooted?”
√242 = √121 x √2
I demonstrated a complete worked example of evaluating a surd and then I rephrased my questions:
“How can I rewrite √48 as a calculation where I have an integer and a non rational number? Say Step 1 then Step 2”
Step 1: √48 = √16 x √3
Step 2: √48 = 4√3
“Why is the integer 4?”
One pupil responded, “because the square root of 16 is 4, Miss.”
Twenty questions later and we were moving on. These were the questions pupils were asked to complete to check they were able to simplify the following surds into the form k√a where k is an integer.
After the exercise, I mentioned that we had previously learnt that when we square root a positive number we get a positive solution, for example √9 is equal to 3. We have also learnt that when finding the solutions of x2 = 9 then we have two solutions -3 and 3. I then posed the question: “Is there a number which I can square where I get a negative answer? If you think so, then on your mini whiteboard have an attempt, and if you think it is not possible then write it down your thoughts in your exercise book.”
Some pupils were determined to find a number that they could square to get a negative result. Some pupils were already light years ahead with an explanation.
In my next post, I shall explain how I introduced the idea of imaginary numbers and structured my teaching in order to enable pupils to solve the two equations outlined at the start using the pre-requisite knowledge showed here. There will be a video and some pictures of pupils’ work too.


Recent Comments