Conception of the good

Today’s post links to my previous post concerning the importance of inflexible knowledge and why it is the foundation of expertise. As a result, it was argued that we should spend a significant amount of time teaching our students topics until the point of mastery.

What I mean by mastery is that students should be able to access key pieces of knowledge from memory, specifically their long term memory, instead of students attempting to complete different calculations in their working memory to solve a problem. For example, students should be able to automatically tell me that the square root of 9 is three, rather than calculating the square root of 9 in their working memory.

It is that time of the year where Year 11 students are frantically revising and, as teachers, our Y11 lessons are spent on consolidating prior knowledge, covering exam techniques and clarifying any existing misconceptions. I have been looking at a few AQA GCSE Maths papers, in order to get my head around how to prepare my students better in the years to come. One evening I decided to complete a past paper and here is what I realised:

We need to ensure that our teaching and learning of the GCSE is seen as a 5 year plan, where in KS3 we teach different concepts to the point of mastery – to the point of memory retrieval.  Inflexible knowledge is the starting point. Can students instantly recall basic times table calculations?  

Let’s look at this question, and my solution to it:

 

In this question here are the different pieces of knowledge I must have had access to in order solve the problem:

 

1) Calculating the lowest common multiple (LCM) of √2, √18 and 1;

2) Multiplying and simplifying surds where √2 x √9 = √18;

3) Adding and subtracting fractions of unlike denominators;

4) Square numbers and square root of numbers from √9 to √900;

5) Rationalising the denominator of a surds in a fraction to present the answer in the form of a√2 where a is an integer;

6) Recognising key mathematical words such as integer; and

7) Simplifying fractions where we divide 126 by 3 to obtain a numerator of 42 and a denominator of √2.

 

Evidently, there is a lot of thinking required to answer this question. There are many logical steps that need to be taken to progress from the problem to the solution. In this case, the difference between students who are experts and those who are novices is that the experts will be able to tell me that the LCM of √2, 18 and 1 is √18. As a result, we must multiply each fraction (numerator and denominator) by a common factor to achieve each fraction in the question to have a like denominator of √18.

The only thinking in working memory should be the logical steps to take from the problem to the solution. Not the calculations to each step – that should be an act of memory retrieval. How can this be achieved?

Only through extensive and distributive practice of finding the LCM of multiple numbers, finding equivalent fractions when adding and subtracting fractions with unlike denominators. This is the first step in the solution, which needs to be recognisable to all students. Automatising procedural knowledge of adding and subtracting fractions is necessary. It is one example of why inflexible knowledge is the bedrock of academic success. Similarly, only by identifying that √9 is equal to 3 can we then change the numerator of the first fraction. Again, inflexible knowledge such as square roots and square numbers represents another step towards the solution.

As teachers, we need to analyse exam papers and problem types, and look at our schemes of work as a five-year plan. How can we structure our teaching and learning to ensure that our students have the necessary background and procedural knowledge to attempt such problems? That these problem types will never be repeated? We cannot get students to memorise a model exam answer. This is not possible and neither is it recommended. We desire our students to see the connection between different concepts, however this is only achieved if students automatise different pieces of inflexible knowledge in the early years of KS3 and only then introduce problem types which connect different concepts.

My next post will outline the practical techniques I have been trialling within my lesson planning for my Y7 class. Watch this space.

 

Knowledge is important – particularly in maths. There are some concepts such as square numbers, where for example 2^2= 4 and 5^2= 25. Students are taught that 2 x 2 = 4 and 5 x 5 = 25. Through extensive repetition and practice, students are able to identify 2^2= 4 because they are no longer processing the calculation: instead they are retrieving this piece of knowledge from their long term memory. It should be an act of memory retrieval. Something I emphasised a lot I my previous blog.

Square numbers are an essential part of Pythagoras’ theorem, but without having any knowledge of Pythagoras’ theorem a student’s knowledge of square numbers is inflexible. Inflexible knowledge is “the unavoidable foundation of expertise, including that part of expertise that enables individuals to solve novel problems by applying existing knowledge to new situations.” (Willingham 2002:32)

I want to emphasise that inflexible knowledge is the foundation of learning. It is vital that we ensure our KS3 students build a bank of knowledge in their long term memory, even if that knowledge is inflexible, because as students start to accumulate knowledge over the years the connections and interplay between different pieces of knowledge allows for deeper learning to develop. This deeper learning in turn induces this bank of ostensibly inflexible knowledge to become flexible.

                

For example, square numbers should be drilled. Students should be able to recite 2^2= 4 and 5^2= 25 without thinking. They should not be processing that calculation; instead, they should retrieve it from long term memory. Now, squaring numbers can be extended to completing calculations such as 2^2 + 5^2 = 4 + 25 = 29. When introducing Pythagoras’ Theorem, students need to be taught that a^2  + b^2 = and that a and b refers to the two lengths which meet at a right angle of a right angled triangle: that the total of both squared lengths is the squared length of the hypotenuse.

Until students take on board this information they cannot proceed with Pythagoras’ Theorem. Once students learn the formula, the application of square numbers evolves into new knowledge; this is flexible knowledge, where “It can be accessed out of the context in which it was learned and applied in new contexts.” (Willingham 2002:32) In KS4, students can start solving questions like this with more ease given that different pieces of knowledge now connect to become flexible:

 

Inflexible knowledge consists essentially of facts, e.g. square numbers, the formula to calculate the area of a circle, and quadratic formula. If given the time to be learnt to the point of memory retrieval, we empower our students to apply such inflexible knowledge to a deeper instruction, e.g. Pythagoras Theorem, the area of a sector, and finding the solution of a quadratic expression. Surely we desire our students to be experts?

If so, we must begin with teaching knowledge – facts – only then will our students become experts and only then will “their store of knowledge…become larger and increasingly flexible, although not immediately.”(Willingham 2002:49)

These increasingly large stores of facts and examples are an important stepping stone to mastery. (Willingham 2002:49)

This second blog post discusses the pedagogy I observed from the brilliant Dani Quinn during my visit at DTA.

Firstly, what is pedagogy? Pedagogy is the art or science of teaching. It is the preparatory training or instruction of how best to teach.

I have been doing a significant amount of reading in the last few weeks of which I am going to refer, whilst discussing the pedagogy I observed.

Learning intention: To be able to calculate the area of a regular hexagon.

Dani started the lesson with a selection of prompt questions to induce students to recall important background knowledge, in this case the characteristics of an equilateral triangle. Following this, students were referred to recalling essential procedural knowledge of how to calculate the area of an equilateral triangle.

Background knowledge consists of essential core facts. Such facts do not change. A triangle is a shape which has three sides. An equilateral triangle has three sides of equal length and has three angles of equal size.

Procedural knowledge “is your knowledge of the mental procedures necessary to execute tasks…[it consists of] a list of what to combine and when.” [Willingham 2009:8]

Below are some of the prompt questions Dani asked, in order to check students’ background knowledge, as something which must be accurate in order to then carry on the lesson:

Figure 1: Equilateral triangle – highlighting essential background knowledge

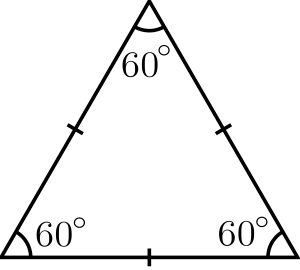
“What facts do we know about an equilateral triangle?”

“What is the size of each angle in this equilateral triangle?”

“What is the name of this length?”

“What is the keyword which describes two lengths that meet at a right angle?”

“What angle does the perpendicular height meet the base length?”

“How can we calculate the perpendicular height of this equilateral triangle given the base height and the slant height?”

“Remind your partner why we need to use Pythagoras theorem in this case when trying to find the area of an equilateral triangle?

 

Here I was witnessing Dani induce students to recall essential knowledge. The thinking process students are engaging in here is essentially memory retrieval, where they are recalling learned facts. This is because “thinking well requires knowing facts.” [Willingham 2009:8] If students do not have the necessary background knowledge embedded in their long term memory then:

 

1. students cannot really consider or attempt the question which, in this case, is how to calculate the area of an equilateral triangle, and then to find the area of a regular hexagon; and
2. their working memories will be overloaded with not only previously learnt information but also novel information that they are interacting with for the first time.

Working memory is your conscious processing part of your mind. It is where you hold information that you are thinking about. Furthermore, it has limitations which your long term memory does not have. Your working memory can effectively process two or three new or to-be learned pieces of information. Whereas your long term memory has no limitations to the amount of information that it can store. Long term memory “is the vast storehouse in which you maintain your factual knowledge of the world…It lies quietly until it is needed, and then enters working memory, and so becomes conscious.” [Willingham 2009:7]

Figure 2. Aitkinson and Shiffrin (1968) Sensory memory-working memory-long term memory model

The prompt questioning students were engaging in was a memory retrieval activity where students were retrieving background knowledge of an equilateral triangle from their long term memory to their working memory. This act of recall not only improves your ability to retrieve information learned previously from your long term memory quickly, but it also means that each and every time you retrieve such background knowledge it will require less thinking – less conscious processing – because your memory is guiding your behaviour. Hence why such questioning is an act of memory retrieval rather than an act of thinking. Students are retrieving factual knowledge from their long term memory, something crucial to engage with for effective learning.

Students recalled basic background knowledge and were able to identify that an equilateral triangle is composed of two right angled triangles; that we divide the base length by two to get the base length of the right angle triangle, and given the slant height of the equilateral triangle being equal to the slant height of the right angle triangle, we can use Pythagoras theorem to calculate the perpendicular height. Dani did not teach any factual knowledge here; she did not need to because students had all this knowledge embedded in their long term memory. They were recalling it all, beautifully.

Figure 3. Calculating the perpendicular height using pythagoras theorem [This image was not used in the lesson – just one that I am using here]

Students guided Dani through a worked example on how to calculate the perpendicular height of an equilateral triangle using Pythagoras theorem. Here students were recalling procedural knowledge. They were recalling “extensive experiences stored in their long term memory in the form of concepts and procedures, known as mental schemas…they retrieve memories of past procedures and solutions,” of where they have calculated the perpendicular height using Pythagoras theorem. [Clark, Kirschner and Sweller 2012:9]

Procedural knowledge is knowledge around the logical steps needed to take to go from the problem to the solution. Extensive practice of solving several problem types allows students to embed such procedural knowledge into long term memory. Again this becomes an act of memory retrieval. Students here are retrieving procedural steps to calculate the perpendicular height from their long term memory to their working memory. Their working memory is not overloaded because they are conscious, processing the problem to already learned information, not to-be-learned information.

 So far:

1. Students had recalled background knowledge of their key characteristics of an equilateral triangle;
2. Students had recalled how to separate an equilateral triangle into two right angle triangles; and
3. Students had recalled how to calculate the perpendicular height using Pythagoras theorem.

Dani subsequently posed this question:

 

“Given that we know the perpendicular height of this equilateral triangle, and the base length, how can we calculate the area of this equilateral triangle?”

Students’ shot up in the air (popcorn technique), because they instantly recalled that to calculate the area of a triangle we multiply the base length and perpendicular height and divide by two. The structure of questioning and sequencing of prior learning carried students to the penultimate stage of the lesson. This is effective pedagogy: it takes into consideration the essential background knowledge and procedural knowledge which needs to be recalled from long term memory, and brought into working memory, in a manner which does not cognitively overload students. It allows students to identify the procedural sequencing of solving a problem type to calculate the area of a regular hexagon.

 The learning intention is to calculate the area of a regular hexagon and everything up to this point has been recall, because the search for the solution of the Learning Intention is where thinking will take place. It is at this point where students will learn new information. They have not been overloaded because the search for the solution is now only starting 35 minutes into the lesson. Students’ working memories are  not being overloaded with storing new information because everything that has been discussed thus far is all learned information. We are not storing new information inasmuch we are about to do so. This hammers home the key point that background knowledge and procedural knowledge is crucial for effective thinking. This also complements the propositions that students cannot begin considering the learning intention without the essential background knowledge discussed above.

Final stage of the lesson:

“Look at this hexagon, can I split it into a number of the same shape?” [Thinking time of 20 seconds]

“Here let me split it into half, and half from a different angle, and now from a different angle? [Here Dani split the hexagon into 6 equilateral triangles] How can I now calculate the area of a hexagon?”

Figure 4. Splitting a regular hexagon into six equilateral triangles

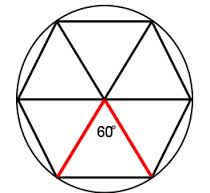
At this point, Richard and I were astonished with the sheer enthusiasm and excitement of students standing up ready to answer the question. At this stage of the lesson Dani introduced new learning. In students’ working memories they were learning new information: that to calculate the area of a regular hexagon we multiply the area of one equilateral triangle by 6.

The lesson was well sequenced. The foundation of academic success was in the recall of essential background knowledge and procedural knowledge. Students were recalling their prior learning, and through extensive practice in their time at DTA were they able to get to this end stage. As they practised a completion exercise on this topic, they were rehearsing new learned information and embedding it into their long term memories.

 

Background knowledge is essential.