On February 15th, the world lost an educator who spent his life developing an approach to accelerate the learning of disadvantaged pupils.

Engelmann was a Marketing Director turned Professor Emeritus of Education at the University of Oregon. He co-authored the famous ‘Theory of Instruction’ with Douglas Carnine and co-developed the term ‘Direct Instruction’ while working with Carl Bereiter. Through grant funding, they set up the Bereiter-Engelmann Pre-school which demonstrated the extent to which disadvantaged pupils could accelerate their learning in comparison to the performance of middle-class pupils.
I have spent the last couple of years becoming familiar with Engelmann’s work, taking aspects of his Theory of Instruction and applying it in my resource creation.
So, what have I learnt from Engelmann?
Answer: That a learner’s inability to respond appropriately to a form of instruction may not be the fault of the child; instead, it can be a problem with what she’s being taught.
This means it’s possible to teach a syllabus in a way she can respond to appropriately without dumbing it down. Here are the four things I keep in mind when creating resources that allow the highest percentage of pupils to understand the course content on the first attempt.
Atomisation
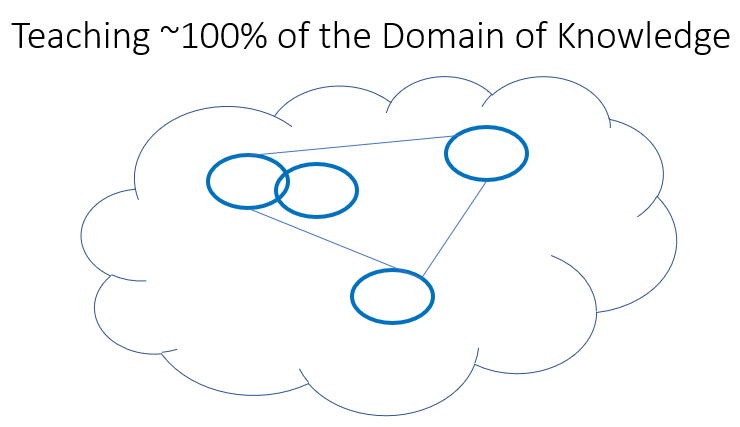
When I used Engelmann’s Connecting Maths Concept textbook series with my Year 7 and Year 8 Intervention pupils, I saw that Engelmann had taken a concept and broken it down into several sub-tasks. A sub-task is a small aspect of a concept. For example, A sub-task of how to add fractions with denominators would be finding the lowest common denominator. For a pupil to develop a flexible understanding of a concept, she needs to be taught as many sub-tasks of the concept and then shown the connections between each of the sub-tasks.
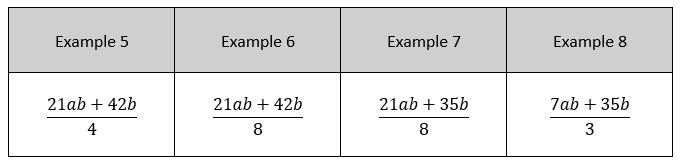
Atomising does exactly this. When I plan a unit of work, I take a concept and break it down into its sub-tasks, and I explicitly teach even the most nuanced aspects of the concept. For example, before I teach pupils how to factorise an expression, I teach pupils how to divide an algebraic expression by an integer, or by an algebraic term. Before I even do this, I teach pupils whether we can also divide an algebraic expression by a number or an algebraic term. An example is shown below:
Here are some examples, of where we can simplify the algebraic fraction:
Here are some examples of where we CANNOT simplify the algebraic fractions because we cannot divide ALL the terms in the fraction:
The value of this exercise is two-fold:
1) Pupils are taught the most nuanced aspects of a concept which are usually the most difficult parts of the unit being taught. If the most challenging part of the concept isn’t taught explicitly then how can we expect pupils to attempt the most complex applications of the concept? We need to be more thorough and comprehensive than you might think and teach the most complex elements of a concept as well as the most basic.
2) Pupils develop a flexible understanding of the concept because they can see the big picture. If you plan an entire unit rather than isolated lessons parts, you are more likely to teach as many sub-tasks as possible and not miss anything that’s essential to a student’s understanding. Missing out sub-tasks inevitably means you have to re-teach. Engelmann set up his textbook series to avoid the need to re-teach. If re-teaching is required, Engelmann provides appropriate correction and reinforcement exercises for each unit of work.
Sequencing the learning in the most effective manner
Engelmann’s Connecting Maths Concept textbook structures the content of a unit of work in just that sequence where the learning can be delivered most effectively. Engelmann believed that all future learning is dependent on prior learning and that there is an optimal sequence for each concept. Provided the lessons are sequenced in the most effective way, pupils always have the knowledge required to access the topic they are about to learn. At United Learning, scheme of work is structured and resourced with the same philosophy in mind. The underlying idea is that how effectively the pupils learn depends on the sequence in which they learn about a particular concept.
Scripting the lessons – Pedagogy
Scripting how you communicate the concept is essential. Now, many teachers despise scripted lessons, and some with good reason, e.g. the script they’re expected to follow is sub-optimal. Another reason for their scepticism is the belief that there is more than one optimal way to teach pupils about a particular concept. However, Engelman persuasively argues that there is only one optimal way to teach a particular concept – and his scripted lessons were field tested with tens of thousands of pupils and constantly being refined in response to feedback. Consequently, he was confident that the scripted lessons he and his colleagues developed embodied the most optimal learning sequences.
When I created my resources at Great Yarmouth Charter Academy, I started scripting how I would communicate concepts, to ensure pupils received the most effective and efficient form of instruction.
Then, I would think carefully about what method to communicate. For example, I didn’t want to teach pupils how to add fractions using a method which was limited to only a few problem types, and then create a different method for another set of problem types. Instead, I tried to create methods that could be applied consistently to as many problem types as possible. This allowed pupils, especially the weakest, to master each concept in all its myriad complexity; evidenced by ever increasing scores in weekly quizzes.
Lastly, my scripted lessons were designed to give pupils the grounding they needed to articulate their understanding. Here is a video showing how a pupil using this knowledge to subtract negative fractions:
Low-stake quizzing and providing appropriate corrections and reinforcements
Engelmann’s Connecting Maths Concept textbook has many opportunities for pupils’ understanding to be tested. The script includes hundreds of questions for teachers to ask. Pupils are given exercises to try with the teacher, as well as independent exercises. Similarly, after every ten lessons, there are also small quizzes recapping what pupils have learnt, not only in the last ten lessons but in the previous 20, even 30.
At Charter, one visitor tallied the number of questions I asked pupils in a single lesson, and they totted up 76 questions in about 25 minutes. I learnt from Engelmann’s teacher scripts how to ask pupils’ questions which test their ability to recall prior knowledge, articulate their knowledge of a concept, to explain a misconception, etc.
In summary, I believe that Engelmann is one of the most important educators of the 20th and 21st Century. I think his work will stand the test of time. By applying his teaching principles to resource creation, I have helped my pupils learn more, and remember it for years to come. My experience confirms, for me, that teacher quality is a function of the resources they have access to. Children are more likely to be successful with a teacher, who has access to exceptional resources, than a teacher who doesn’t, and never has.
Engelmann’s work has taught me more than any educator that I studied with during my PGCE and MA. My next post will look into the evidence for the effectiveness of Engelmann’s approach and the reasons why his work hasn’t been more influential.
After my podcast with Craig Barton, I have received many emails asking to share more booklets. I have attached the booklets that I made during my time at Charter. They aren’t perfect, and with my current workload, I am not in a position to refine them. However, I do think they are useful for teachers who want to start designing their own booklets. I used each booklet with all my classes. I hope they are helpful.
There will inevitably be mistakes in the booklets. I take full responsibility for any errors that you see.
https://drive.google.com/open?id=16UtxWsL3T5M2wz65YjwfRYyJ3BZSNZZp




















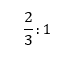
Recent Comments