I saw a couple of tweets asking teachers how they plan their lessons, what is a typical lesson look like, what happens behind the scenes? I was keen to read people’s responses and then to be able to compare it to how I have been planning my lessons over the years. This blog post will outline the typical planning process and I will use an example: substituting fractions.
Before I begin, I thought it would be useful to know that during the planning process I outline a progression model. I pick a topic that I want to teach, e.g. substitution, and I break down the topic into complex skills which I want to teach and form exercises which pupils will complete. Breaking down each skill into small component skills prevents pupils overloading their working memory during the initial stages of teaching new information.
Recap
The start of every lesson I give pupils a selection of questions to recap what has been taught over the last few days. Pupils do this on their mini-whiteboards. This is a quick exercise taking no more than 5-10 minutes. The questions have been prepared in advance because I want to ask questions which really test a pupil’s understanding. There is no point giving pupils a question to do on their mini-whiteboards which they will all more definitely get right. You want to tease out any confused understanding or misconceptions that pupils may have. This is because if a pupil proceeds to learn new content with misconceptions in mind then more misconceptions will form, or become consolidated.
Recap: Required pre-requisite knowledge
Recapping prior knowledge is essential. If pupils don’t have prior knowledge that future learning depends on then no successful learning will take place, and furthermore pupils will be cognitively overloaded from learning multiple skills. The core knowledge that needs to be recapped will be used again and again throughout the lesson when learning new content. Before I taught pupils how to substitute fractions into different expressions I recapped how to :
- Add and subtract fractions with common denominators
- Multiply fractions
- Multiply fractions and integers
- Divide fractions
- Add and subtract fractions with different denominators
Initial Teacher Instruction: Faultless Communication
I will think about the worked examples that I want to use to teach pupils how to substitute fractions in a manner which works for all problem types. Engelmann refers to this form of instruction as Faultless communication which I shall blog about soon. I try and design my teacher instruction so nothing that I say contradicts what I have taught in the past.
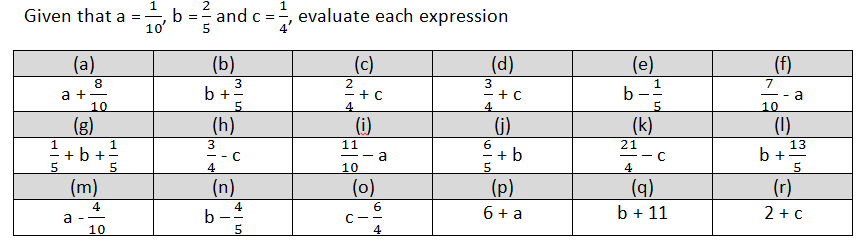
I want to teach pupils how to substitute fractions into different expressions. I plan my worked examples and I think about how I can design them so pupils can see that the process of how to substitute a fraction into an expression is always the same. The process is the same when I am substituting (adding and subtracting fractions with common denominators):
- two different fractions
- three fractions
- if the result after substitution gives me a fraction which I can simplify to an integer
- if the result after substitution gives me a negative result
- if the result after substitution gives me zero
- if the result after substitution gives me a mixed number
I will also pre-empt misconceptions:
- Question A: “When we add or subtract fractions with the common denominators. The denominators are the same, the denominator remains the same, add or subtract the numerators.”
- Question O: “I have ¼ – 6/4 they are going in different directions, I find the difference which is 5/4. The larger fraction is negative so my result is also negative
- Question G: “Here I have three terms that is ok. I can have questions like this…
- Question I: “I have eleven-tenths minus one-tenths and the result is ten-tenths which simplifies to 1. That is correct. That is possible.”
- Question P: “I am adding an integer to a fraction so my result is a mixed number. That is correct. That is possible.”
Not showing these examples means that when pupils try the following questions then they will be freaked out by getting answers which are negative or zero or mixed numbers. The process of substituting fractions where you have to add or subtract fractions with common denominators is the same regardless of the question set up or the answer you get.
Show Call
After going through my worked examples, I will give pupils a very similar set of questions to attempt on their mini-whiteboards. Here pupils are showing their written work to maximise the likelihood of pupils creating perfect answers and working out during independent work. I put a question on the board; give pupils 30 seconds to complete the work on their mini whiteboards. They hold their mini-whiteboards with the answer hidden so other pupils can’t copy each other. I then ask them to show me all at the same time – 3, 2, 1 and show. This lets me see all 32 pupils’ working out. I will give whole class feedback over mistakes that I see. I will show the class a pupil’s work if it is excellent. I will show a sub-optimal answer too and stay ‘Jonny, would have gotten a merit if he had done this…’ or ‘Jonny can improve this. Who can help him improve this? Thank you for letting us all learn from your work Jonny.’ Doug Lemov goes into more detail about the effectiveness of Show Call in his podcast with Craig Barton.
The purpose of this exercise is for me to fix any mistakes and close those gaps. Also, to identify the pupils who are still struggling and support them during the independent practice part of the lesson.
Independent Work
I will have designed a practice exercise of questions for pupils to attempt independently. I will circulate the room. Help pupils who are struggling. Glance at pupil work as I go around and fix any mistakes that I spot. At the end of this timed exercise I will read out the answers and get pupils to tell me how they did:
“Raise your hand if you got 10 or more questions correct. 15 or more. 20 or more. All correct so far.”
“If you made a mistake but you now understand that mistake raise your hand please.”
“If you made a mistake that you don’t’ understand and want me to go through it on the board then raise your hand. We can all learn from you.”
No Plenary
I don’t usually have plenaries in my lessons. I plan my lessons so pupils can complete all the exercises, even more so the hard staff at the end that I want pupils to have the time to complete. I don’t use Exit Tickets because I do a weekly quiz which informs me of the same information that an Exit Ticket does.
Reflections
I think this approach is similar to many teachers. Nothing here is extraordinary but ordinary. However, what is most important to understand is that the typical lesson above includes features and details that allow pupils to learn, and more importantly it allows pupils to remember what they have learnt. Everything that I have outlined is a combination of what I saw as good teaching from my own education but also from what I have witnessed and learnt from many exemplary teachers that have kindly let me watch them teach.



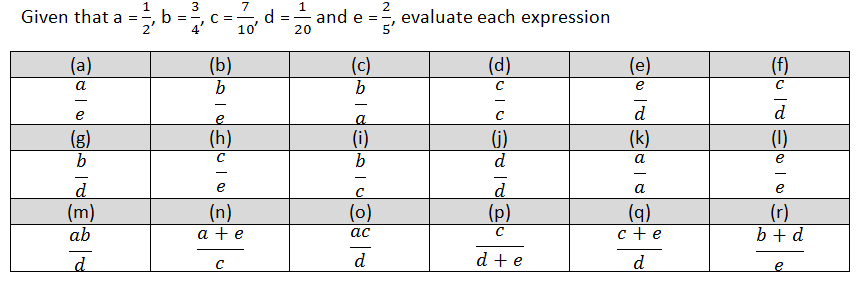







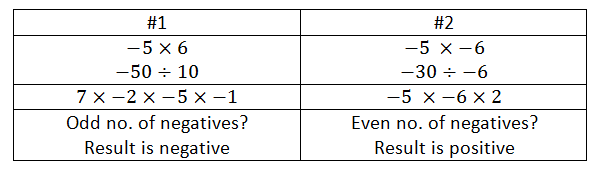


Recent Comments