This blog post is the third of a series ‘Reattempting Circle Theorems’. We have looked at the following circle theorem and a non-circle theorem:
Circle Theorem #1: A right angle triangle in a semi-circle
Show that: Two radii and a chord form an Isosceles Triangle
We will now look at the next circle theorem:
Circle Theorem #3: A cyclic quadrilateral’s opposite angles add to 180 degrees
The booklet attached below follows the same structure:
- Starting with the circle and outlining its features to deduce the circle theorem
- Show a series of examples and non-examples of the circle theorem
- Start with examples to find the missing angle(s) of
- the circle theorem in isolation
- interleaved basic angle facts
- interleaved previously taught circle theorems
- Algebraic section (In this case, I haven’t attached it because I would do it differently now)
Introducing the Circle Theorem: A cyclic quadrilateral’s opposite angles add up to 180 degrees
Here is a circle:
Then we draw four points on the circumference of the circle:
We draw a straight line between one point and the next point on the circumference. We can go clockwise or anti-clockwise when choosing which points to connect:

And keep going:
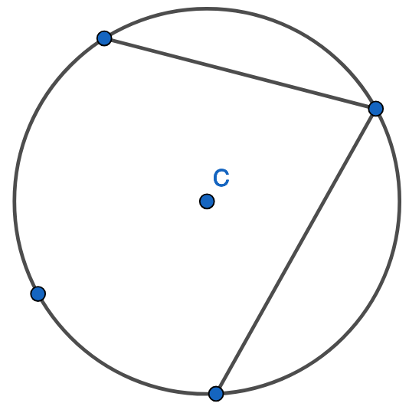
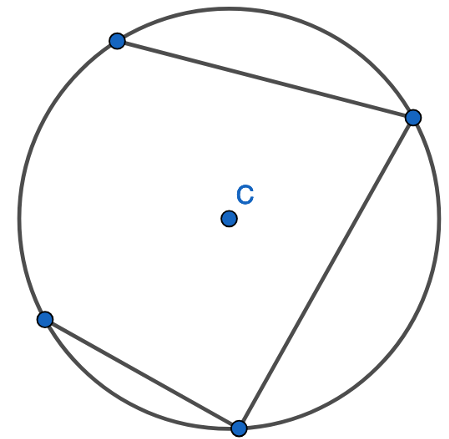
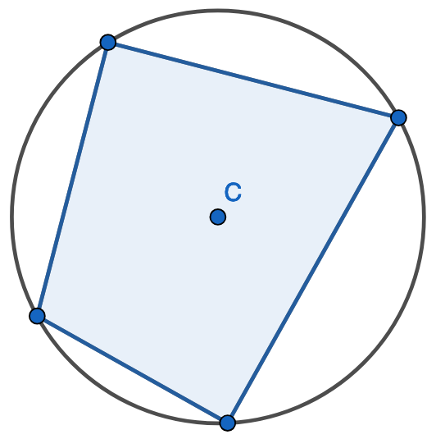
All four corners of the four-sided shape lie on the circumference. This is a cyclic quadrilateral.
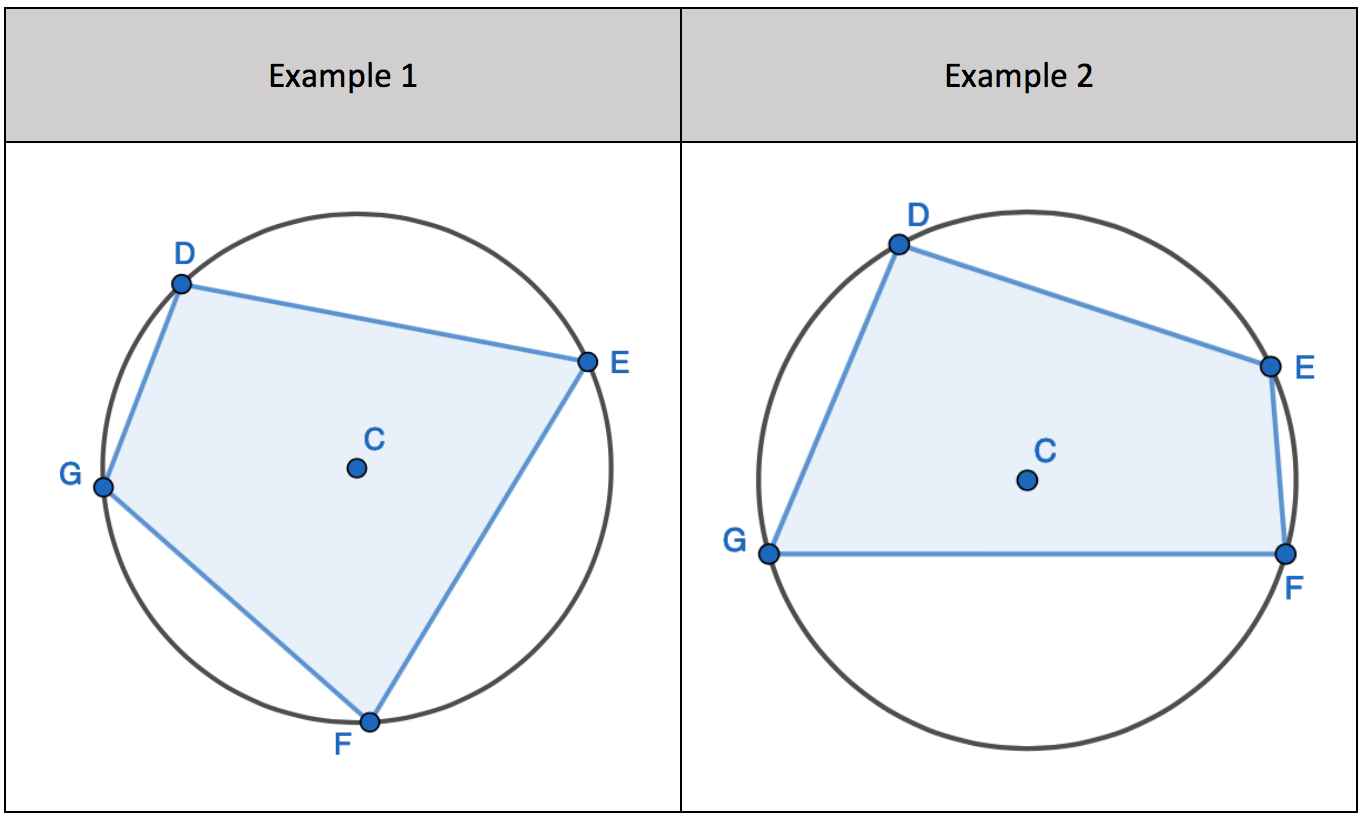
Here we have a four-sided shape. A quadrilateral where all four corners of the shape lie on the circumference of the circle. Here is another example:
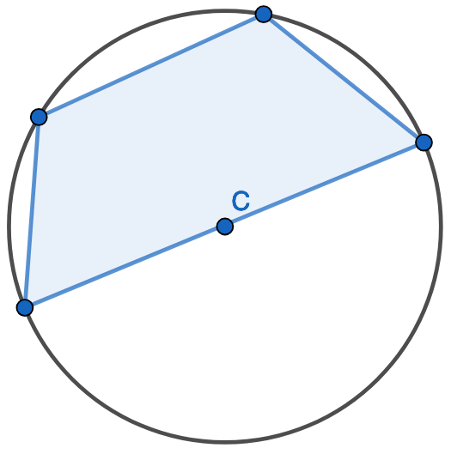
All four corners of the four-sided shape lie on the circumference. This is a cyclic quadrilateral.
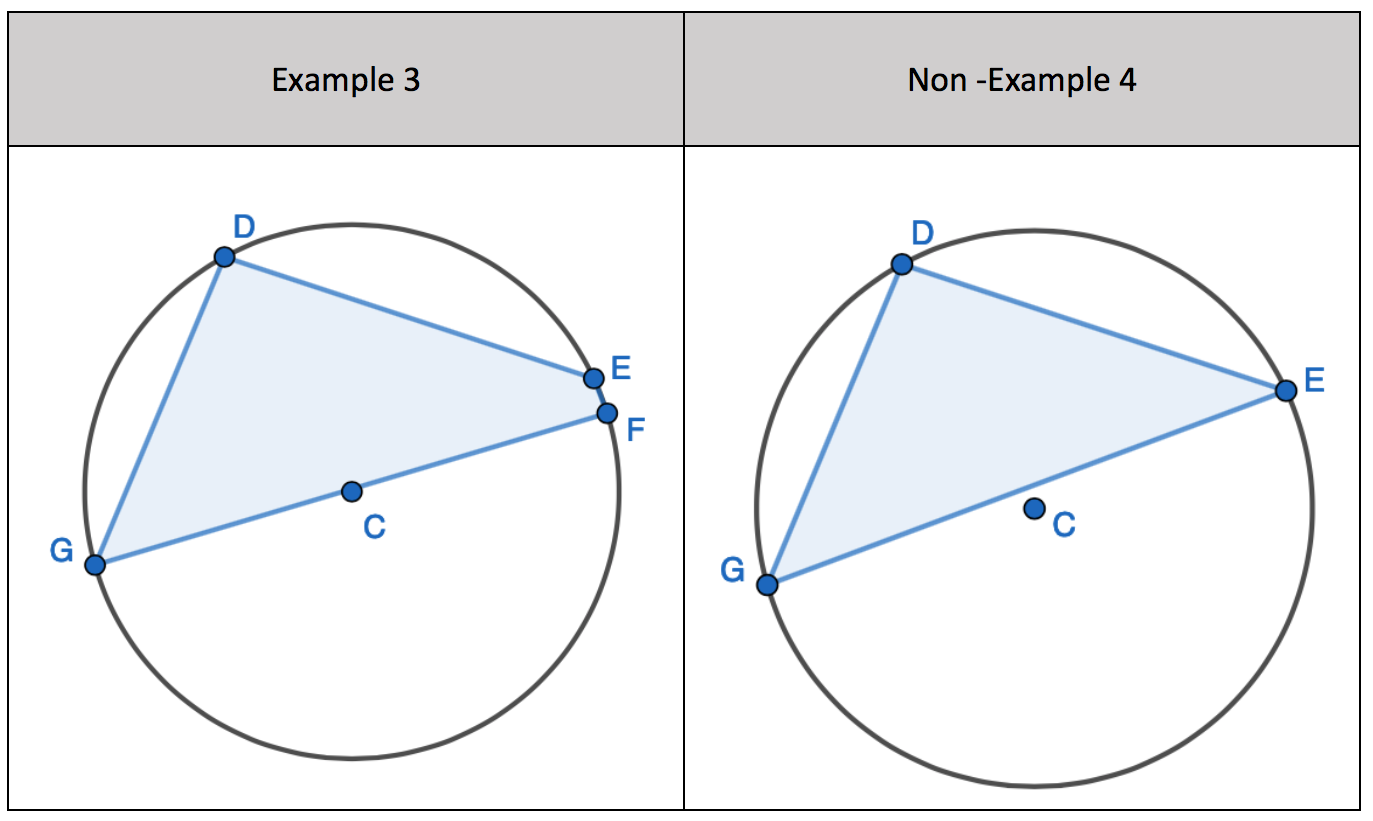
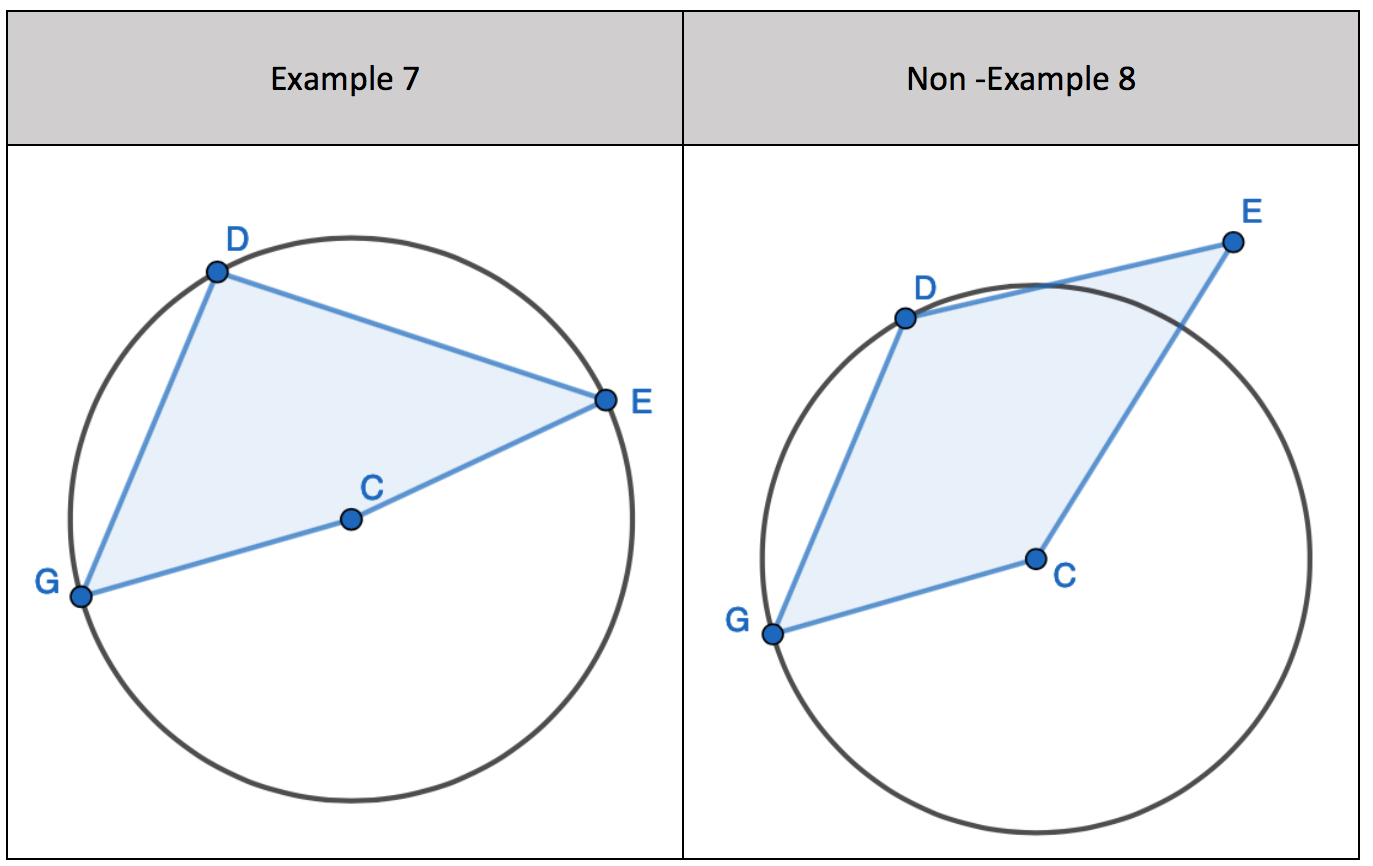
Here is an example of a quadrilateral but NOT all its corners lie on the circumference. Here one of the corners is the centre of the circle; this isn’t on the circumference of the circle. This is not a cyclic quadrilateral.
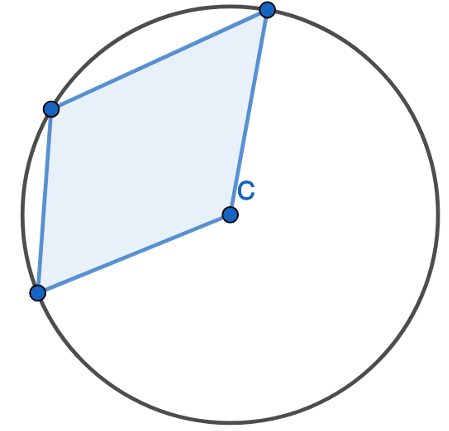
All four corners of the four-sided shape DO NOT lie on the circumference. This is NOT a cyclic quadrilateral.
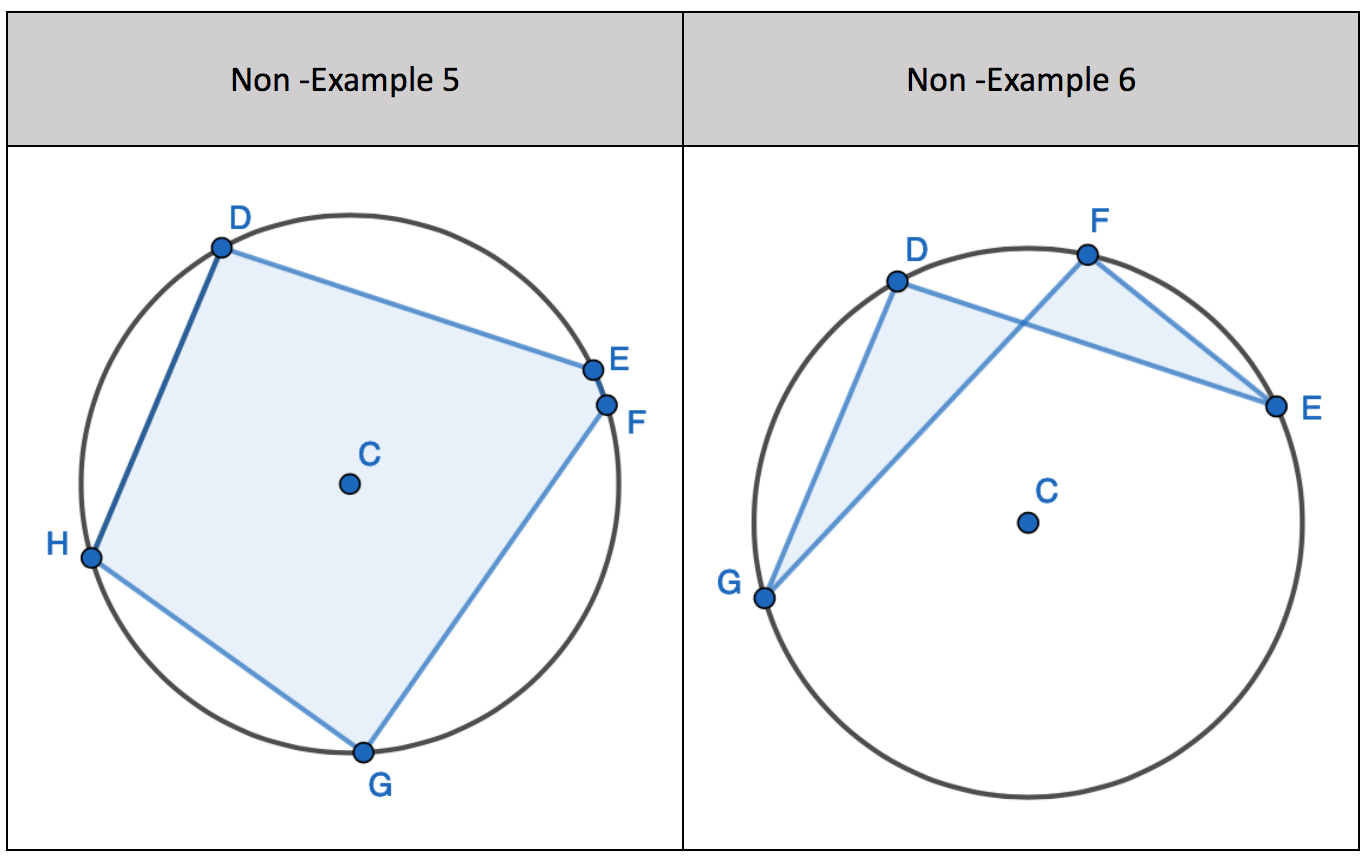
Here we do have four corners of a shape on the circumference of the circle, but the shape doesn’t have four sides. This is not a cyclic quadrilateral.
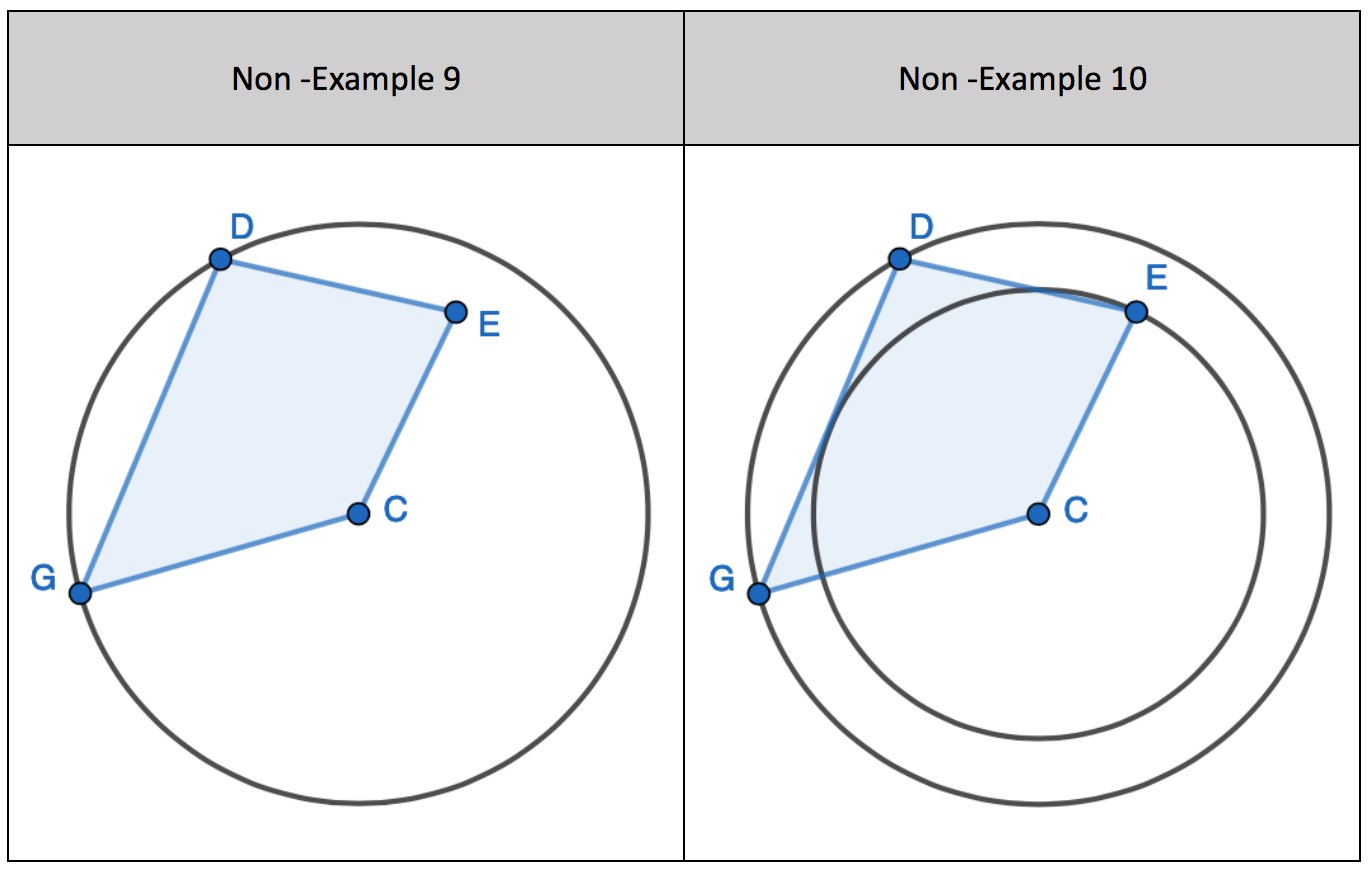
Examples and Non-Examples of the Circle Theorem
Specify the language to state the correct circle theorem examples and its non-example.
For example:
“All four corners are on the circumference then we have a cyclic quadrilateral.”
For a non-example:
“Not all four corners on the circumference then we don’t have a cyclic quadrilateral.”
“The shape doesn’t have four side lengths even though all four corners are on the circumference. We don’t have a cyclic quadrilateral.”
Find the missing angle using the Circle Theorem
At this point, I would state the steps to find the missing angle before looking at a few examples. Pupils can follow the steps if they lose track during the example explanation.
Here are the steps:
- Check that the shape is a four-sided shape and all four corners lie on the circumference
- Identify the opposite angles in a cyclic quadrilateral
- If you have one the opposite angles, then subtract from 180oto find the unknown missing angle
Here are the teacher examples to find a missing angle or angles. The variation between the examples isn’t evident here. I try to change one change at a time between the ‘I do’, and the ‘We do’ example. I’ll explain the thinking behind choosing each example:
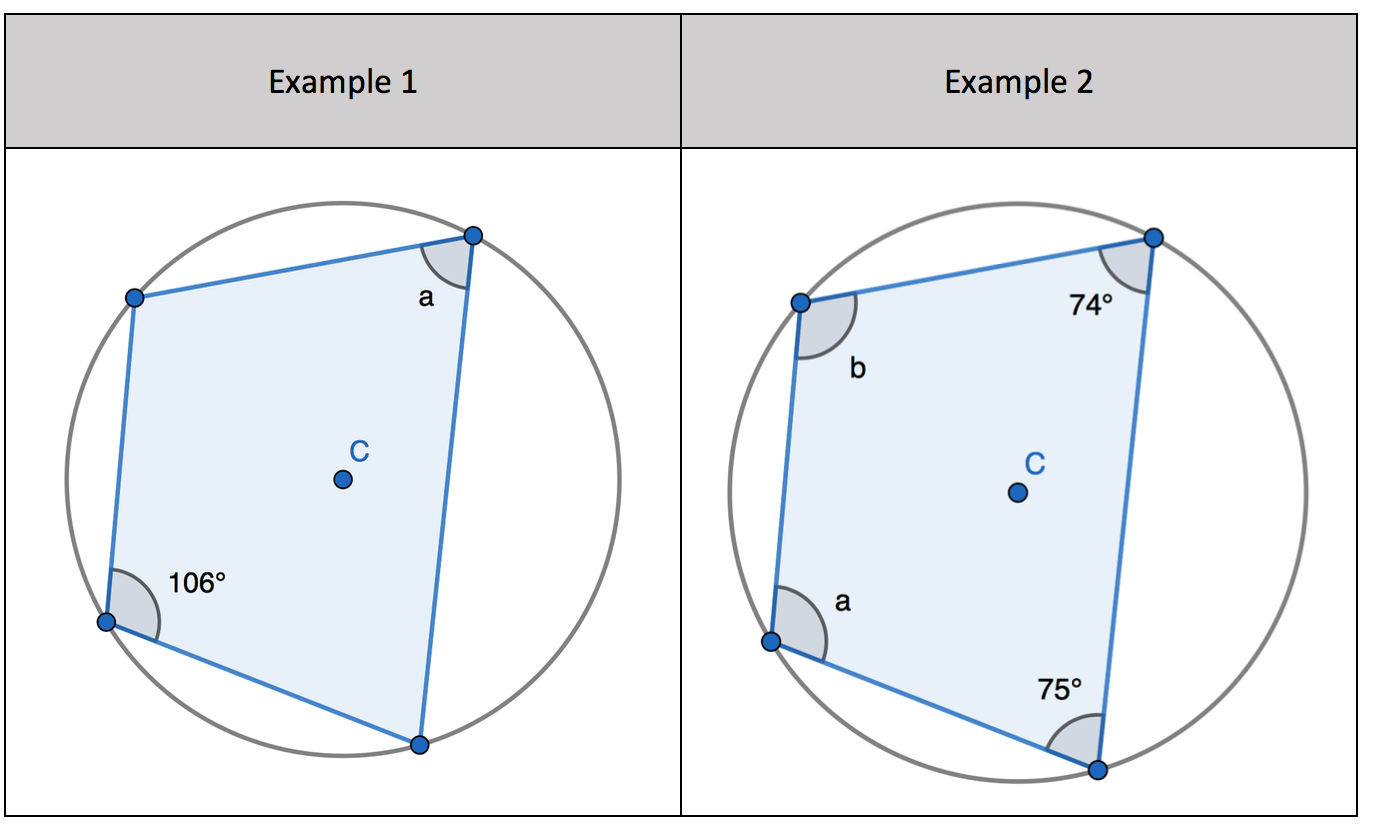 1. Find the opposite angle in the quadrilateral by subtracting the angle you have from 180 degrees
1. Find the opposite angle in the quadrilateral by subtracting the angle you have from 180 degrees
2. Find the opposite angle in the quadrilateral by subtracting the angle you have from 180 degrees. Two incomplete pairs of opposite angles.
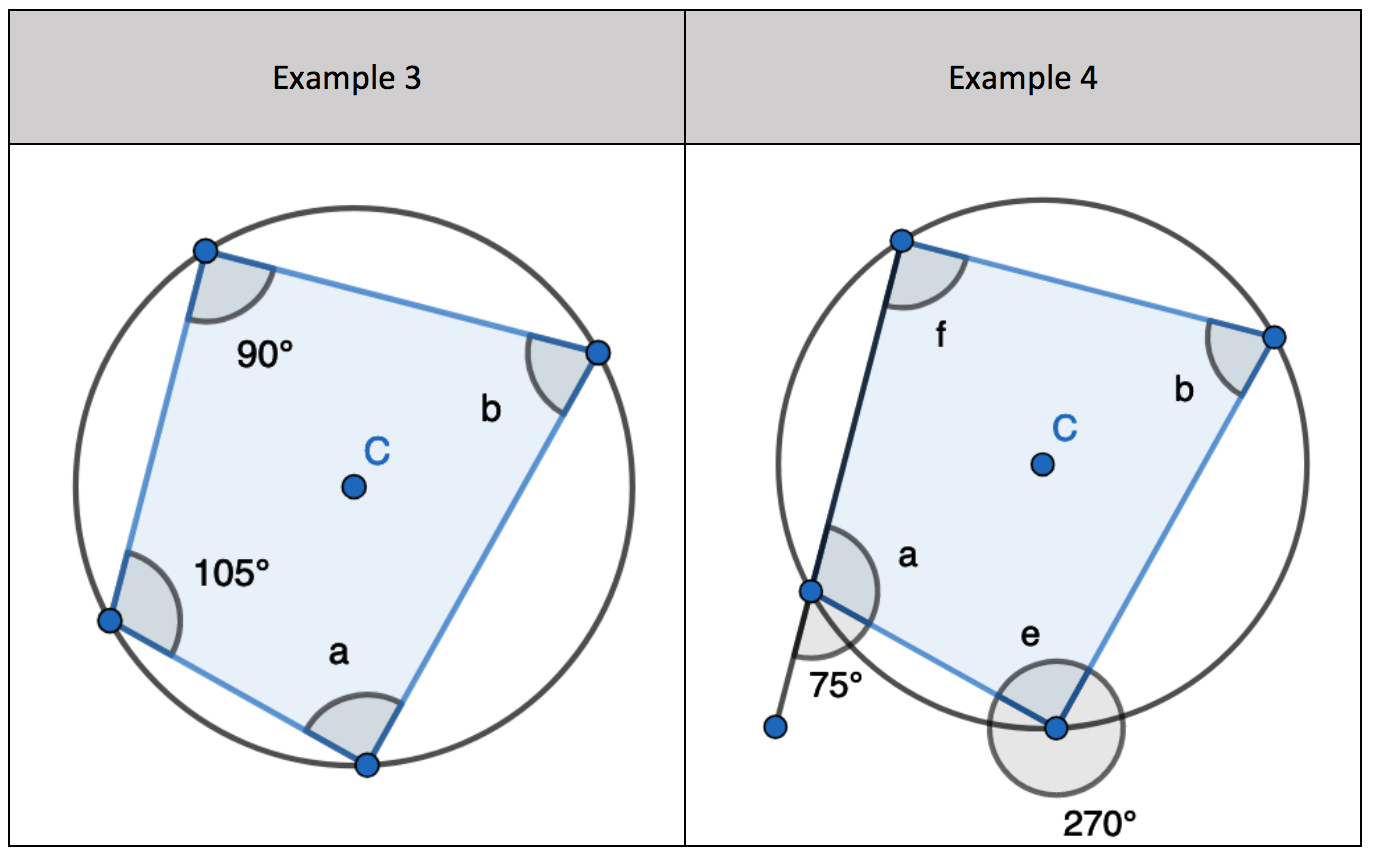
3. Find the opposite angle in the quadrilateral by subtracting the angle you have from 180 degrees
4. Using basic angle facts. Find one of the opposite pair of angles in the quadrilateral to find the second missing opposite angle.
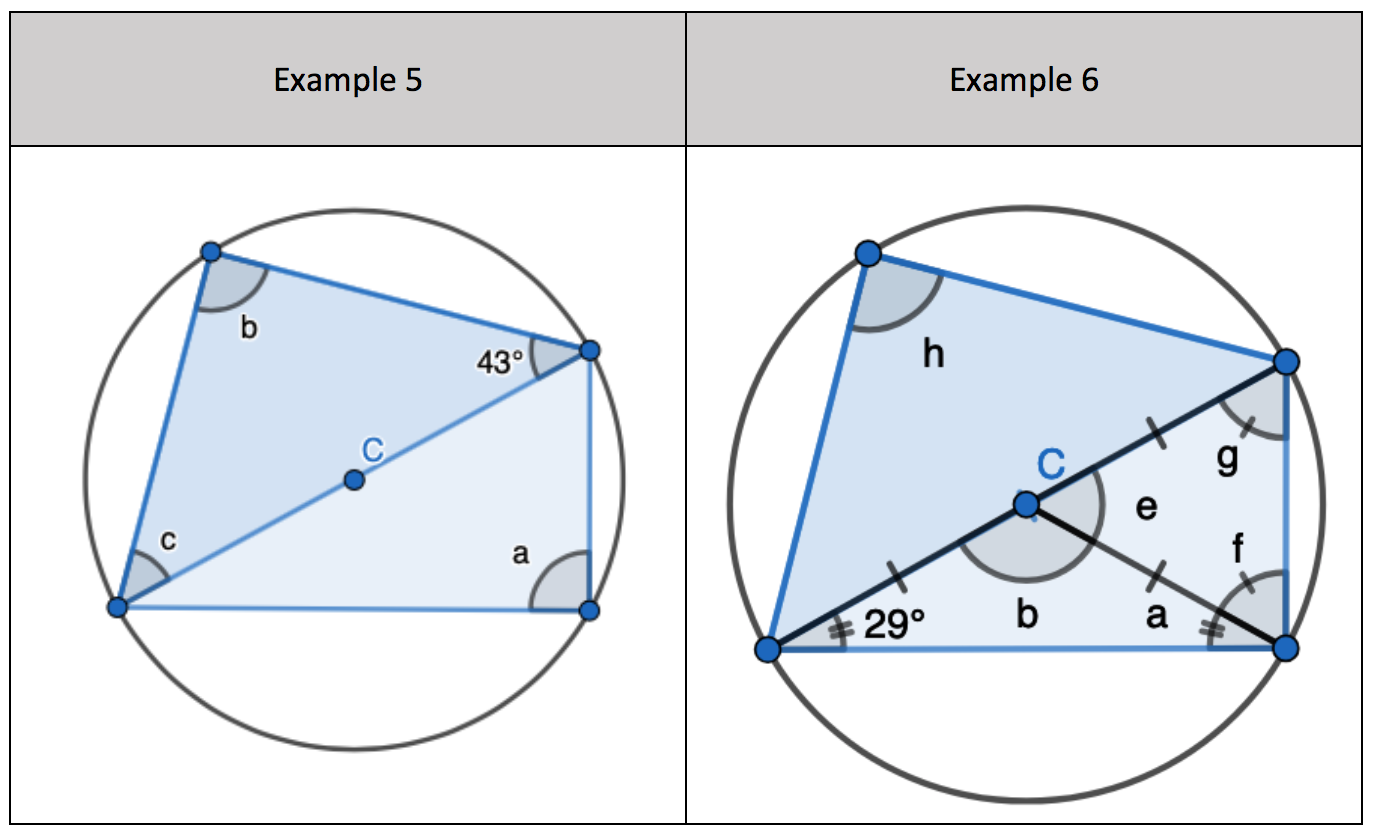 5. Interleaving the first circle theorem – A right angle triangle in a semi-circle
5. Interleaving the first circle theorem – A right angle triangle in a semi-circle
- Identify ‘a’ and ‘b’ as a right angle of 90 degrees.
- Find ‘c’ by adding 90 and 43 degrees and then subtracting from 180 degrees.
6. Interleaving the first circle theorem – A right angle triangle in a semi-circle. Interleave the ‘show that’ feature of two radii and a chord form an Isosceles triangle
- Identify ‘h’ as a right angle of 90 degrees.
- Identify the total of ‘a’ and ‘f’ as 90 degrees.
- Find ‘a’ as 29 degrees as it is one of the two equal angles in an Isosceles triangle
- Find ‘b’ by adding the two equal size angles and subtracting the result from 180 degrees.
- Find ‘e’ by subtracting ‘b’ from 180 degrees using the basic angle fact that angles on a straight-line sum to 180 degrees.
- Find ‘g’ and ‘f’ by subtracting ‘e’ from 180 degrees and dividing the result by 2.
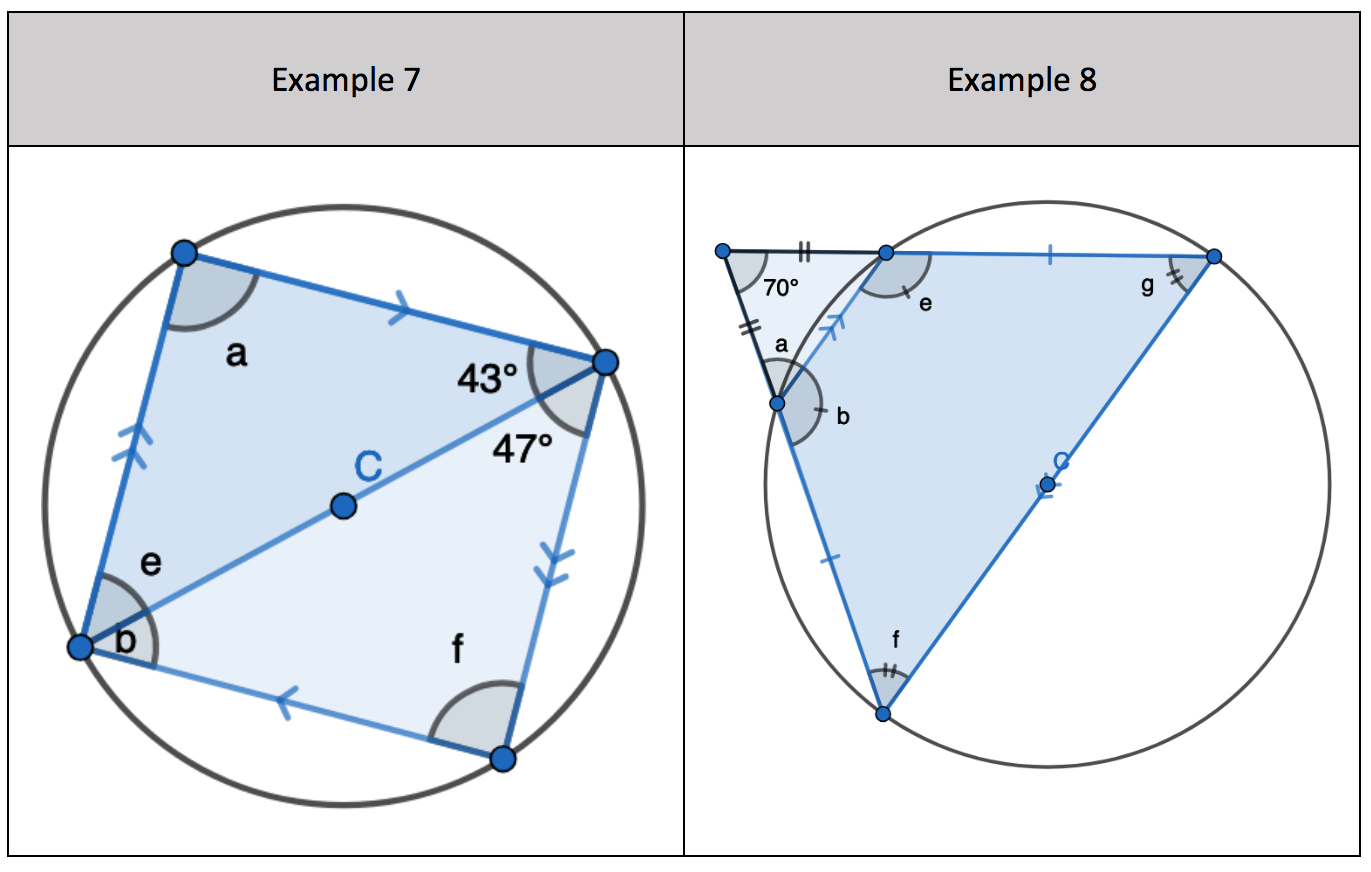 7. Interleaving the first circle theorem – A right angle triangle in a semi-circle
7. Interleaving the first circle theorem – A right angle triangle in a semi-circle
- Identify ‘a’ and ‘f’ as a right angle of 90 degrees
- Find ‘e’ by adding 90 and 43 degrees and then subtracting from 180 degrees
- Find ‘b’ by adding 90 and 47 degrees and then subtracting from 180 degrees
- Different approach: Interleaving angles on parallel lines to determine ‘b’ as an alternate angle to 43 degrees. And ‘e’ as an alternate angle to 47 degrees.
8. Interleaving basic angle facts to
- Find ‘a’ since the triangle is an Isosceles triangle
- Find ‘f’ and ‘g’ as they are corresponding angles to ‘a’
- Find ‘b’ by subtracting ‘a’ from 180 degrees since angles on a straight-line sum to 180 degrees
- Find ‘e’ since its equal to ‘b’ because the shape is an Isosceles trapezium.
Booklet attached:
https://drive.google.com/file/d/1RAQIj84hPiPHuwptk-L98kd_KX0aEZ-c/view?usp=sharing
Leave a Reply
You must be logged in to post a comment.