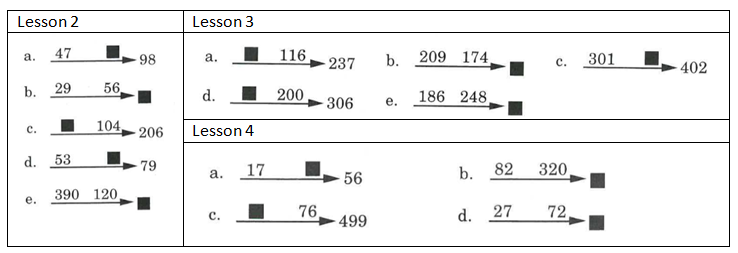
During my second year at Michaela Community School, the department used Siegfried Engelmann’s Connecting Maths Concept Textbook series as the main teaching tool for Intervention.
This is the third write-up of a sequence of blog posts:
- Introducing the number family
- Manipulating the number family for complex worded problems
- Just when you thought the problems couldn’t get more difficult
In my last post, I outlined how Engelmann teaches pupils within his textbook series of the relationship between addition and subtraction using the number family. Furthermore, how the set-up of a number family is utilised by pupils to answer complex worded problems.
This blog post will go through the most difficult problem types using the number family set up that were taught.
- Problem Type #4: Number families with fractions and integers
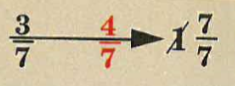
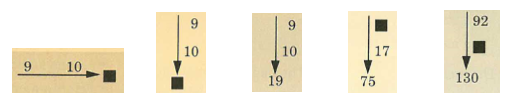
By Lesson 67, fractions were included in the number family calculation. For example:
If a number family shows a fraction and a whole number, you have to change the whole number into a fraction.
The bottom number of the fraction you change the whole number into is the same as the bottom number of the fraction in the family.
The above sentences in bold are directly lifted from the teacher presentation book
Here’s a number family with a fraction and a whole number:
This is taught after pupils have learnt and practised the following:
- Writing an integer as a fraction with a specific denominator
- Simplifying fractions into integers
- Differentiating between fractions that do and do not simplify to an integer
- Subtracting fractions which have common denominators
The teaching of the above then allows such a problem type to be taught.
To have further similar questions included in Test 7
Similarly, including problems in Lesson 72:
2. Problem Type #5: End up, Out and In
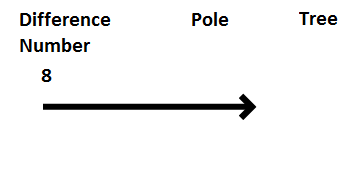
The next number family problem that is introduced tells pupils about getting more and then getting less of an amount. The number family has three fixed categories: End up, Out and In.
Here is an example before I explain the set up of the problem type:
End up is the first small number. The big number is the number that goes in. The next number small number is shown by the number for out. Whatever is left is referred to the number that you end up with. It is the difference between the number for in and the number for out.
Then the problem type became more complicated because more terms were added to the number family, For example:
Fran had $36. Then her mother paid her $12 for working around the house. She spent some money and ended up with $14. How much did she spend.
Here you have two values for in that you must find the total of: 36 + 12 = 48. The total is the big number which is labelled under in. We know how much Fran ends up with so this is what is left.
The sequencing of this problem type and the transition between the first example to the second example with multiple terms is gradual for pupils to learn without experiencing cognitive overload.
The first example of the problem type is only taught in the teacher-led part of the lesson, it is not set as independent work for pupils to do. I think this is simply because it is very difficult for the weakest pupils to complete by themselves that to ensure success it is taught with teacher assistance. Also, pupils did find this hard to learn! There is a lot of reading, a lot of information to organise but by the end of the year pupils were able to do this will little to none teacher assistance. It may be covered in the next set of Engelmann books that follow after this set.
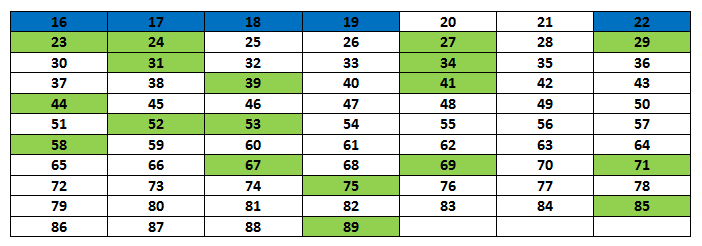
We can see the distribution of how the problem type is covered over different lessons.
Blue = Teacher-led exercise using prepared script + teacher-guided qus
Green = Independent task where pupils are being tested
White = not present in the teacher-led exercise or independent task
End up, Out and In
End up, Out and In with multiple terms
Conclusion
Here we can see the progression in difficulty from taking the most simple addition and subtraction calculations and introducing more complex problem types were addition and subtraction are being tested in various ways. Furthermore, Engelmann looks into including visual variations of the problem type, including large integers and fractions, and multiple terms. Yet, each and every time the algorithmic set-up of structuring the information using a number family allows pupils to draw the correct inference about what they need to do next – Do I add or subtract?
Next, I shall be looking at the teaching of fractions!



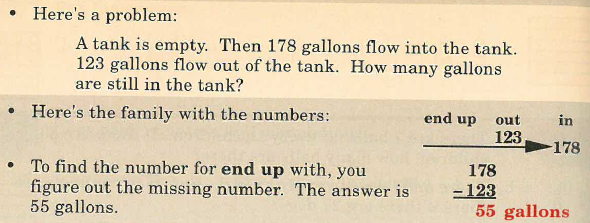
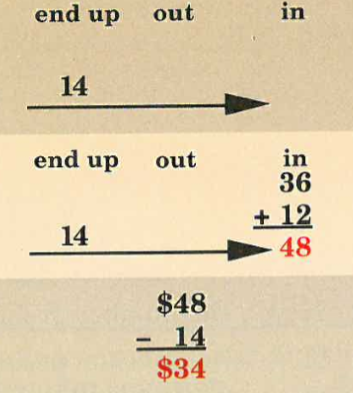

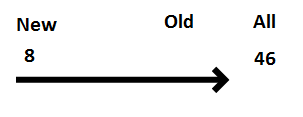




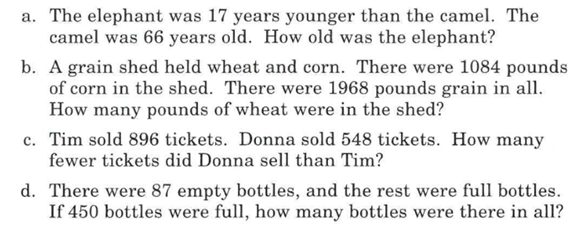






Recent Comments