During my second year at Michaela Community School, the department used Siegfried Engelmann’s Connecting Maths Concept Textbook series as the main teaching tool for Intervention.
This is the second write-up of a sequence of blog posts:
- Introducing the number family
- Manipulating the number family for complex worded problems
- Just when you thought the problems couldn’t get more difficult
In my last post, I outlined how Engelmann teaches pupils within his textbook series of the relationship between addition and subtraction using the number family.
This post will go through how the set-up of a number family is utilised by pupils to answer complex worded problems.
- Problem Type #1: P and Not P questions
In Lesson 16, P and P’ problems were introduced. For example:
There were 8 new shows. The rest were old shoes. There were 46 shoes in all. How many shoes were old shoes?
The number family problem has been written up into words where pupils need to do the following:
- Label the three groups; P, P’ and all. In this case, New, Old and All
- Assign the number stated to the correct group
- Decide whether to add or subtract to form the calculation
It is explained in the presentation book how to deliver the teaching of such a problem type. Then the following questions are given to follow throughout future lessons: 2. Problem type #2: More than or Less than problems
2. Problem type #2: More than or Less than problems
In Lesson 24, a problem type is introduced which has a new layer of complexity, pupils need to:
a) Learn the terminology of difference words: more than, less than, greater than, smaller than
b) position labels and numbers on the number family arrow by understanding the difference words of more than, less than etc.
Here are some examples:
- If you know that one value is more than another value then that one value is the big number. The other number is the small number. E.g. 14 is more than 11. 14 is more. It’s the big number. 11 is one of the small numbers.
Second example:
- If you know that one value is less than another value then that one value is the small number. The other number is the big number. E.g. 24 is less than 30. 24 is less. It’s the small number. 30 is the big number.
Pupils are also taught to write the smaller value as the second small number. This is deliberately mentioned in the Teacher’s presentation book. Pupils are learning how to use the number family to interpret the question. This can be extended to similar questions where pupils are taught to structure the calculation before performing it:
The presentation book emphasises the importance of the key words: shorter, heavier, fewer, further etc. These words indicate which item will be the small number label and which item will be the big number label.
In regards to question a, the pole is shorter than the tree so the pole is the small number label and the tree is the big number label. The number 8 is referred to as the difference number, this is deliberate language used within the Teacher presentation book. The difference number is the first small number label. The number before the difference word (8 feet), in this case shorter than, is the difference number.
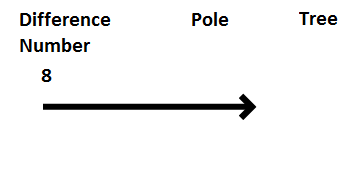 The next three lessons pupils are taught how to label and structure the number family. They do not perform any calculations they just place each label and the difference number given. Lesson 28 they are taught to perform the calculation fully. For example,
The next three lessons pupils are taught how to label and structure the number family. They do not perform any calculations they just place each label and the difference number given. Lesson 28 they are taught to perform the calculation fully. For example,
The calf weighed 345 pounds less than the horse. The horse weighed 509 pounds. How many pounds did the calf weigh?
3. Problem Type #3: Asking to find the difference number
By lesson 43, there are number family problems that ask about the difference number. For example: A coat cost $134. A radio cost $23. What is the difference in the price of these objects?
Pupils are being asked to compare the cost of two items. Using the number family set up a pupil positions the big number and the small number. In this case the coat costs more than the radio. They also learn that the small number is the second small number too. The first small number is the difference number.
4. Differentiating between problem type
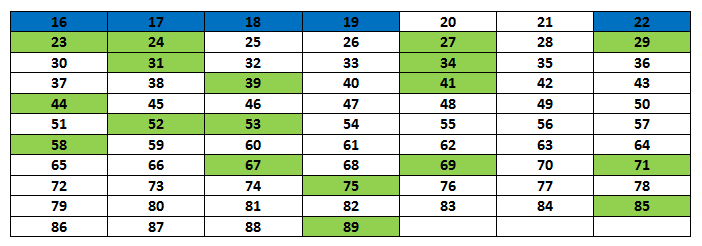
By Lesson 43, an exercise to differentiate between problem types is introduced:
Similarly, what is interesting to note in regards to the distribution in the teaching of these problem types and the spread of independent practice exercises is that what is mostly practised is the P and Not P problem types. I think this is because it is the first worded problem type that pupils use the number family to reach the answer.
Blue = Teacher-led exercise using prepared script + teacher-guided qus
Green = Independent task where pupils are being tested
White = not present in the teacher-led exercise or independent task
Each number represents the Lesson no. E.g 16 = Lesson 16
In the next post, I will go into the problem types that became progressively more difficult yet were simple to answer because of the set-up of a number family.
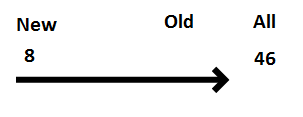



Leave a Reply
You must be logged in to post a comment.