In my last series of blog posts I outlined how Siegfried Engelmann teaches the relationship between addition and subtraction using the number family.
This blog post was inspired by an epiphany whilst teaching a very weak pupil basic addition. I had taught her the following in a sequence of lessons:
- Adding integers with no carrying
- Adding integers with carrying
- Adding decimals with same number of decimal places (carrying)
- Adding decimals but with varying number of decimal places (carrying)
In the last half of a lesson I was teaching pupils how to attempt the following set of problems.
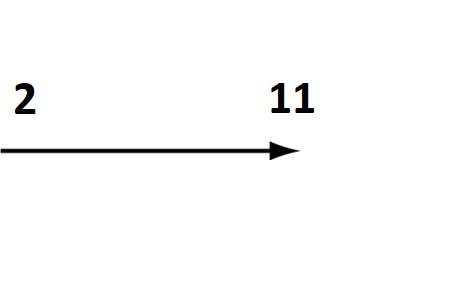
I explained using the last problem that when I am adding 2 in the units column to the 9 I am not really getting 1, instead I am getting 11, and the tens is being carried to the column on the left. All pupils besides two understood this. I then demonstrated using a number family that:
- 2 is the small number
- I am adding 9 which is the second small number
- To get a big number. This big number must be bigger than the two small numbers.
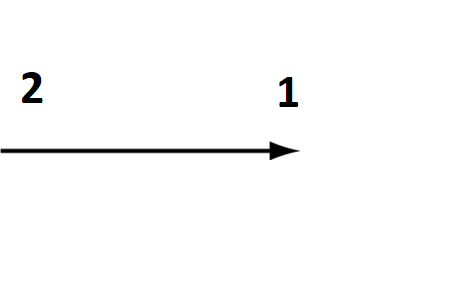
I also showed a non-example of the number family:
- 2 is the small number
- I am adding 9 which is the second small number
- I will have a big number at the end of the arrow. It can’t be 1 because the big number cannot be smaller than the two small numbers.
At this point, she got it. This is my weakest pupil in year 7. I definitely underestimated how powerful the number family structure can be!


Recent Comments