Engelmann’s, Theory of Instruction, introduces the concept of Faultless Communication. It is a form of communication which conveys only one interpretation of the concept at a time. The result of this is having the learner either respond by learning the intended concept, or the learner fails to do so. Faultless communication is designed in a manner where the learner’s performance is framed as the dependent variable. Faultless Communication also
“rules out the possibility that the learner’s ability to respond appropriately to the presentation, or to generalise in the predicted way, is caused by a flawed communication rather than by learner characteristics.”
For this to be the case, some assumptions have to be made about the learner:
Assumption 1:The capacity to learn any quality is exemplified through examples
Assumption 2:The capacity to generalise to new examples is on the basis of sameness of quality (and only on the basis of sameness)
Structuring Examples
The examples that are chosen demonstrate a quality of sameness of a concept, and such communication, as outlined in Engelmann’s Theory of Instruction, must meet these structural conditions:
- The examples present only one identifiable sameness in quality – not more than one
- The communication requires a signal for the quality of sameness that each example demonstrates. A second signal is also required to identify the examples that do not share the quality of sameness.
- The examples chosen must demonstrate the range of variation that typifies the concept. Each positive example will be slightly different from each other but the examples will all share the quality that is to be generalised.
- Negative examples, as well as positive examples, must be shown to show the limits of variation in quality that is permissible for a given concept.
- The communication must provide a test to check whether the learner has received the information provided by the sequence of examples.
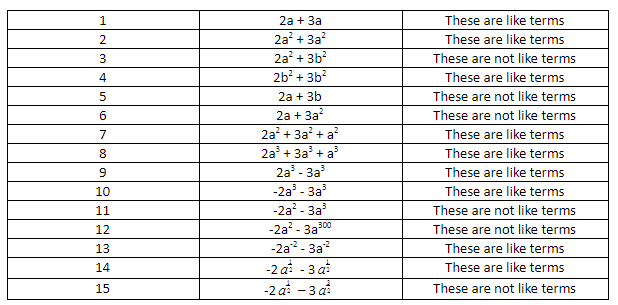
Here are a few examples of teaching sequences that I have used in the last week to communicate which terms are like terms:
In regards to the conditions stated above, this sequence meets the conditions because:
- It is communicating one quality of sameness – exactly the same unknown in each term
- There are two signals, one for the positive examples and one for the negative examples
- There is a wide variation that typifies the concept, negative terms, integer powers, fractional powers, negative powers etc. I could potentially include more examples with decimal powers etc.
- Negative examples have been included and positioned deliberately within the sequence to contrast with the example presented before.
- A test was given to follow.
How did the lesson proceed?
After getting the pupils to do a mini-quiz on whiteboards to identify whether the following group of terms within the expression were like terms or not like terms. I went through a series of teaching examples of how to collect terms to write one expression in its simplified form. In this lesson, pupils learnt how to:
- Differentiate between like terms and unlike terms within an expression
- Simplify an expression by collecting the like terms.
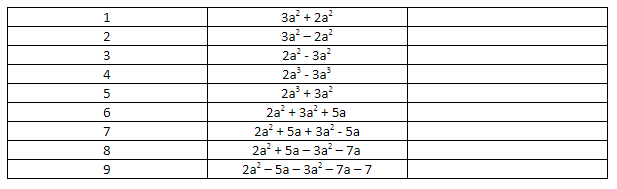
Here is the teaching sequence of examples used to teach the second point:
Pupils attempted to collect like terms on their mini-whiteboards using the following set of examples:
A few key points to mention here: I deliberately gave pupils examples where they had to collect negative terms. I taught pupils that the sign on the left side of the term was part of that term. For example, in regards to example 2, a pupil would say:
Pupil: The two like terms are a^2 and 4a
Pupil: The unlike term is -5a
I wanted pupils to practise adding negative terms because that is what pupils struggle with the most when learning how to collect like terms. My examples gradually escalated in difficulty but that difficulty is important for pupils to practice with the teacher.
In regards to example 6, I wanted pupils to see that when two terms give a result of 0, we don’t write 0a^2b and we don’t need to write + 0 to the simplified expression.
This was the second set of teaching examples that were used to collect like terms where a term had more than one variable:
There are some topics in Mathematics where it is easier to create an sequence of teaching examples in line with the structural conditions of Faultless Communication.
I attempted to apply the a similar structure when teaching Year 11 how to change the subject of a two step equation where the desired subject either has a power or root. Here is my attempt:
Make ‘f’ the subject:
- The quality of sameness I attempted to demonstrate was that when you list out the order of operations of what happens to ‘f’ we reverse that order. For example, I have ‘f’, I square it, then add 2. Now, I reverse the order of operations. Therefore, I first subtract 2 on both sides of the equal sign, and then square root both sides of the equal sign. The sameness was in the procedure that pupils used to change the subject of the equation.
- There is no signal that I used here because It wasn’t applicable for what I was intending on teaching – how to change the subject of an equation.
- The examples demonstrate that the if I add 2, subtract 2, multiply by 2, divide by 2 I will always reverse the order of operations of what happens to the desired subject.
- I didn’t have a set of negative examples because it wasn’t applicable for what I was intending on teaching.
- There was a test of similar examples to attempt
I do think it isn’t always possible to create a sequence of examples which meet all the structural conditions of Faultless Communication. The example where pupils learn how to rearrange the subject of an equation is a perfect example of this. However, what I have done is take some of the structural conditions which are applicable and applied that to create a sequence of examples. It is possible to design a better set than the one above where all conditions are met.
Final Reflection
Faultless communication has allowed me to design a sequence of teaching examples and questions for pupils to attempt on mini-whiteboards which allow pupils to infer the correct generalisation with the highest percentage of pupils understanding what has been taught on the first attempt. The intended concept has been taught and pupils have been able to take what they have learnt and apply it to an independent practice exercise. I am finding this to be successful with my classes of all abilities. This is simply an attempt of applying Engelmann’s work from his Theory of Instruction within the classroom. From what I have seen in terms of pupil work, it has been working. I hope this to be something I continue to use in my planning.



Recent Comments