Teachers spend hours creating their own resources for their pupils to use after a concept has been taught. Over the years, I have made lots of resources which I change every year, simply because I think this exercise won’t help this set of pupils grasp the concept being taught. I’m now at a point where I can make an exercise of questions which all pupils can use to learn the intended concept. What has changed for me? I have developed a better understanding and can now apply principles of variation theory when creating resources. This has allowed me to use the same practice exercise with all my classes.
Variation Theory
Variation Theory is posited on the view that “when certain aspects of a phenomenon vary which its other aspects are kept constant, those aspects vary are discerned.” (Lo, Chik & Pang 2006:3) It has been previously pointed out that “to see or experience a concept in a certain way requires the learner to be aware of certain features which are critical to be the intended way of seeing this concept.” (Lo and Marton 2012) Here is an example, I am attempting to teach pupils how to factorise a quadratic expression. The critical aspect I want pupils to focus on is determining the factors of ‘c’ that sum to give the ‘b’ coefficient. I have kept the ‘a’ coefficient the same, and I have kept the ‘c’ constant the same too. I want pupils to work on the aspect that the ‘b’ coefficient is always the sum of two factors of the constant.  Here is a similar example:
Here is a similar example: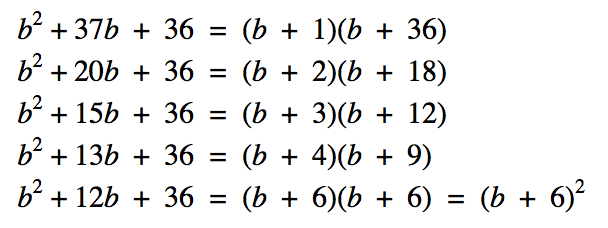
Here is another example, but here I am focusing pupils’ attention on the critical aspect of determining the factors that multiply to give the ‘c’ constant. The factors will always sum to 10 which is the ‘b’ coefficient.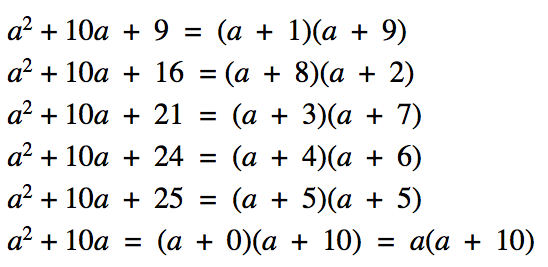
I have deliberately included the last example. Where pupils are taught that two numbers that add to give 10, but the product will be 0. I have included it at the end because it is a nuanced example of the set of expressions above. It is nuanced because its explicit features are not visible for pupils. It does not follow the structure of (a + __)(a + __) because the bracket of (a + 0) = a
What about introducing a practice exercise where you want pupils to focus on their negative mental arithmetic? The critical aspect for pupils to focus on is determining the factors of -24 that sum to give the ‘b’ coefficient stated.
What I really like about the above exercises is that pupils are experiencing different forms of variation from the previous set of expressions. However, in this practice exercise, I have changed only one aspect of each expression, which is the focal point of the intended concept being taught. If I change both the ‘c’ and ‘b’ coefficients of a quadratic expression then I am asking pupils to make two decisions, essentially to focus on two different things, two numbers that sum to ‘b’ and the same two numbers that multiply to ‘c’. This above exercises constrains a pupil’s thinking deliberately for two expressions at a time so the intended process of factorising a quadratic expression becomes clear. They can also see how the negative arithmetic changes the value of the ‘b’ coefficient.
I can now bring a practice exercise where pupils are now able to put their understanding of how to factorise a quadratic expression to the test:
A few key points about the design of this exercise set:
- I have only changed one aspect of each expression from the previous expression.
- I have focused on changing the surface of each expression. The procedural process is the same.
- Between (b) and (c) I have deliberately changed the focus from finding the sum of the constant’s factors to then finding the product of two factors of 12 that also give a sum of the ‘b’ coefficient.
- I have structured the calculation for the coefficients of ‘b’ and ‘c’ because I want pupils to explicitly see how they are determining the numbers that go into the factorised form. I wanted pupils to see the depth underneath the surface of each quadratic expression. I also want pupils to see the procedural relationship between the factorised form and its quadratic expression.
To summarise, this is simply an attempt to widely implement variation theory when resourcing. I have seen that pupils are able to draw the intended mathematical understanding being taught sooner. A greater proportion of the class are able to apply their understanding of the intended concept correctly. The design of this exercise also aids pupils to deliberately think and apply their understanding at each expression they had to factorise. The above exercise is an improvement from previous exercises I have made in the past, and can be improved further after seeing how pupils respond to it.
Paper used: http://www.cimt.org.uk/journal/lai.pdf
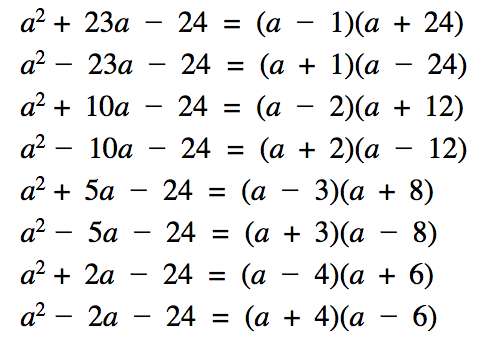

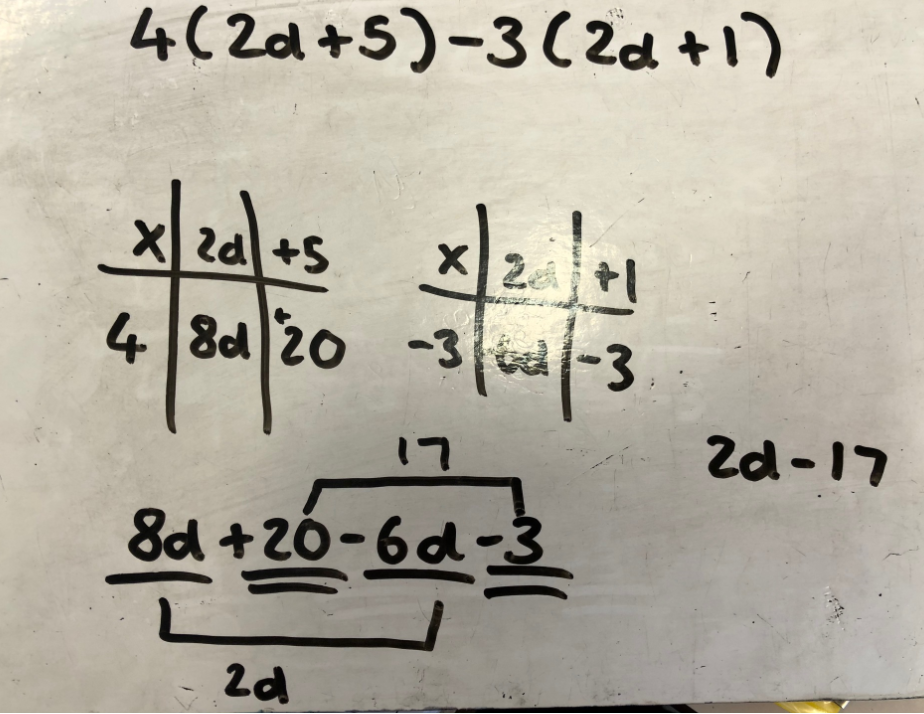
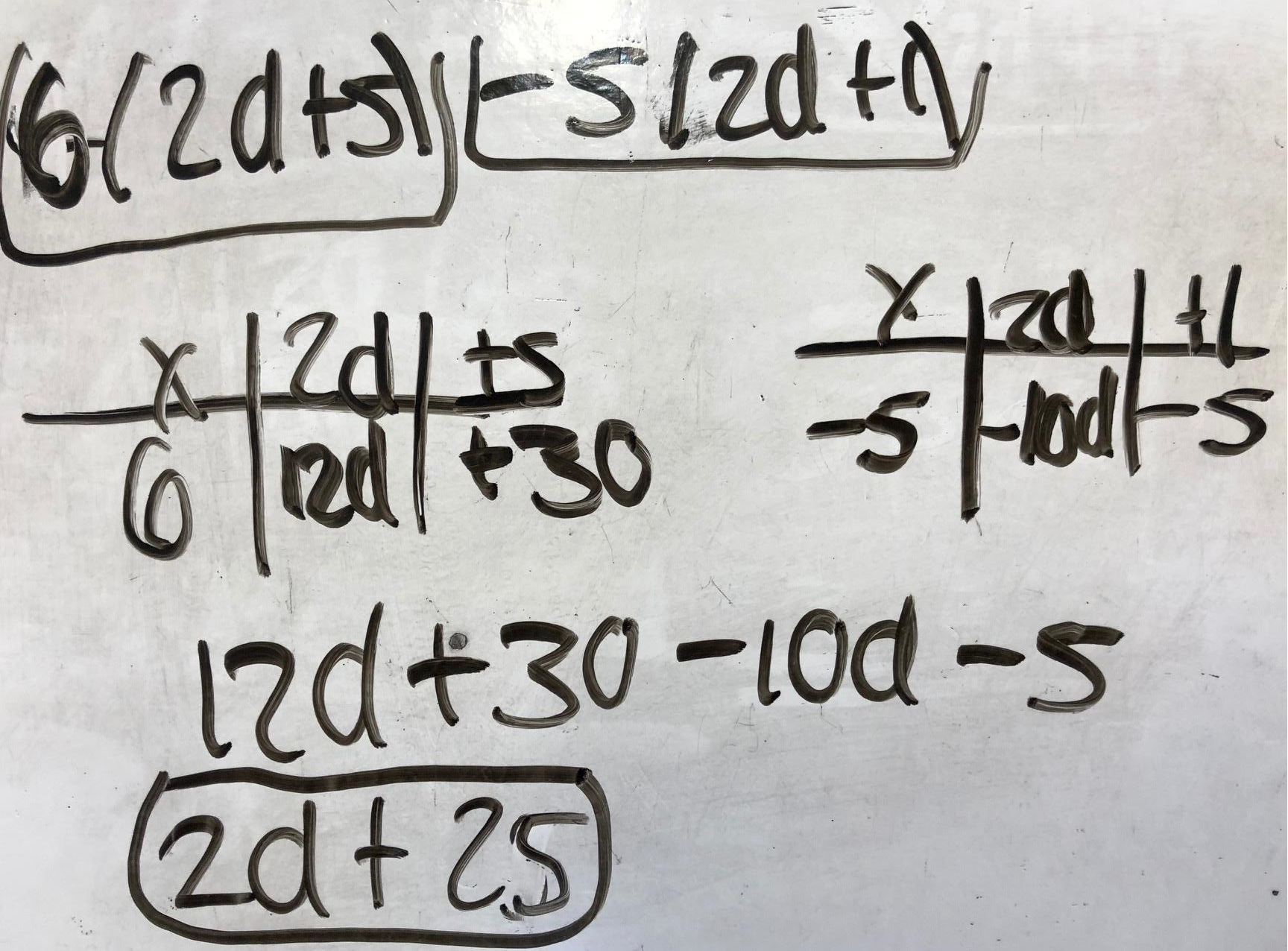
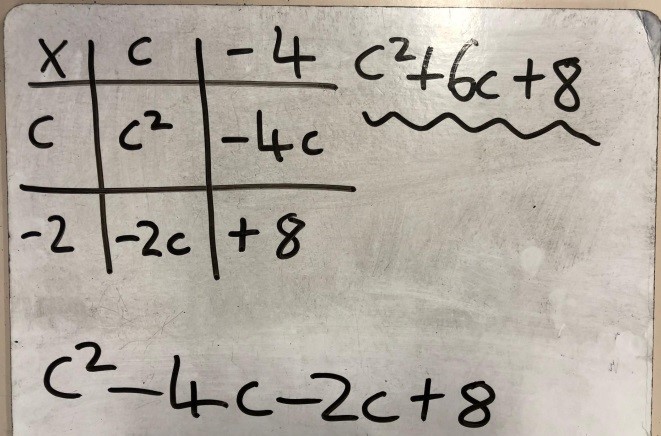
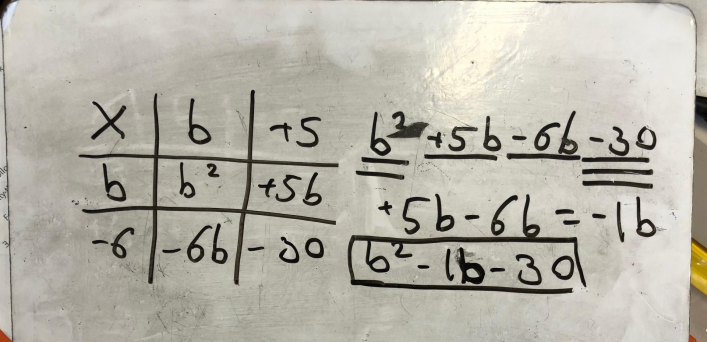
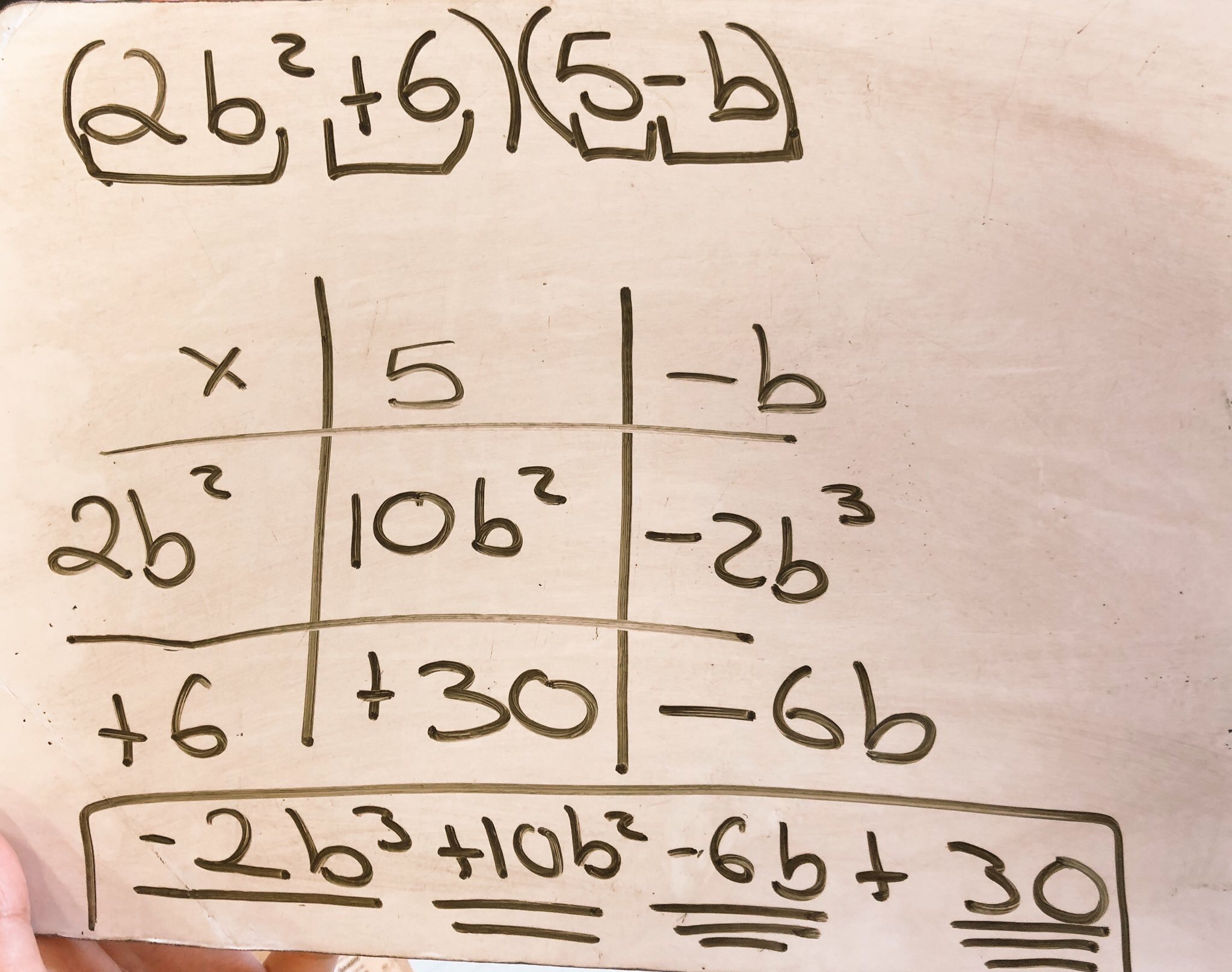
Recent Comments