This blog post is the last of four posts outlining the teaching and sequencing of various fractions skills taught in the Connecting Maths Concept Textbook series. Specifically, Level D. The first blog post can be found here. The second post can be found here. The third post can be found here. The following content was shown at La Salle’s National Mathematics Conference in Kettering.
16. Deciding whether to multiply by more than one or less than one
This is one of my favourite component skills taught in the Level D textbook series. In this exercise pupils needed to identify whether what we multiply the first integer by is more than 1, less than 1 or equal to 1 depending on the result of the calculation.
If you multiply by more than one you end up with more than you start out with.
If you multiply by less than one you end up with less than what you start out with.
Pupils did find this difficult to learn. I did breakdown the questioning further in addition to what was stated in the teacher presentation book.
1.Which number is bigger?
2.What number is smaller?
3.Am I going from a big number to a small number? Yes or No?
4.Am I going from a small number to a big number? Yes or No?
5.If I am going from a big number to a small number, then I am multiplying by less than 1.
6.If I am going from a small number to a big number, then I am multiplying by more than 1.
Pupils were also taught that if the value in the calculation is equivalent to the value in the answer then I have multiplied by 1. This was understood because of learning about equivalent fractions where you multiply by a fraction which can simplify to one.
The reason why I really enjoyed teaching this was due to the rigour of the exercises. The design of the exercise below is pure genius. It gets kids to think whether a fraction less than 1 is smaller than an integer, or which fraction is smaller out two fractions with the same denominator.
In regards to question (d), pupils are able to write seven-sevenths as an integer equal to 1. They are seeing that they are going from a small value to a big value so we are multiplying by more than
For question (e), pupils write the fraction of twenty-seven-ninths as an integer before they determine whether they multiply by more than 1, equal to 1, or less than one.
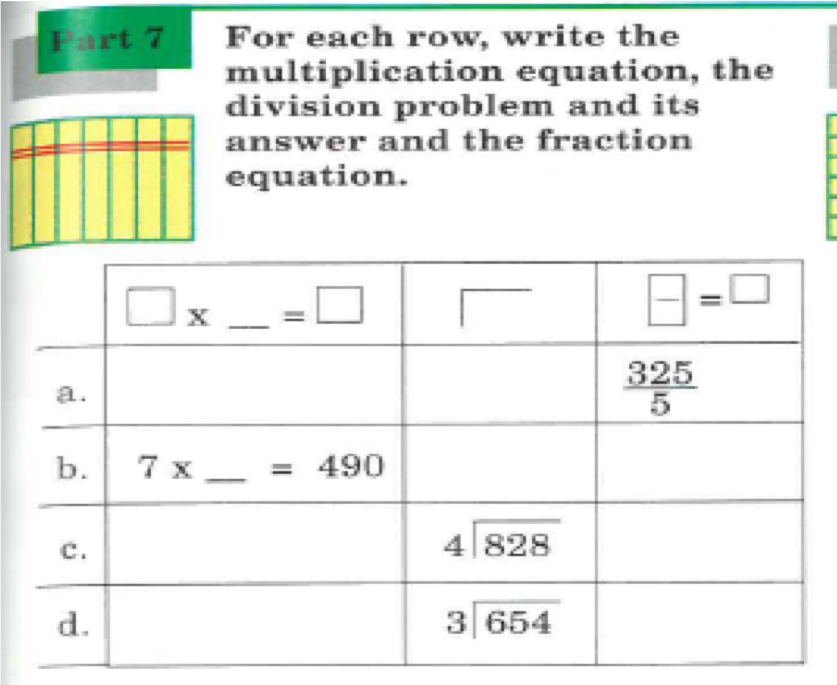
17. Multiple Representations
Pupils are identifying the relationship between multiplication and division by showing division calculations as a reverse multiplication calculation, a fraction and the bus stop method.
There are exercises which pupils are given a calculation in one form and they need to write it into the other format. I really value exercises like this because when pupils complete mathematics problems in their GCSE or A Level exam papers that they can write their answer as a fraction, or divide the top and bottom to write it as a decimal etc. I just recently marked my Year 11 mock papers and it was lovely to see that so many pupils were able to see that when solving to find a value that they saw it as a fraction, that they would then use the bus stop method to write the fraction’s value as an integer or decimal. This wasn’t the case in their paper workings from their first round of mocks in November.
18. Demonstrating equivalence
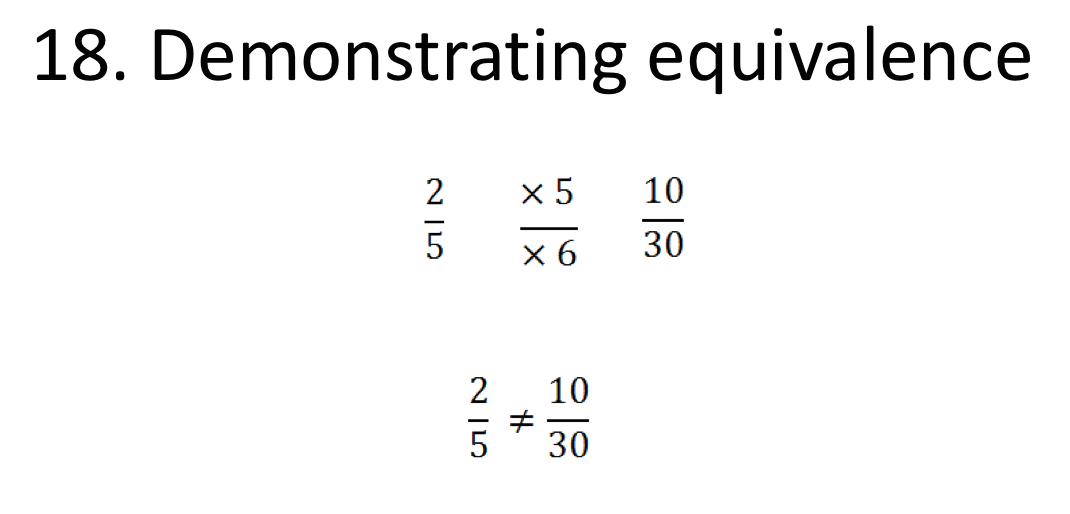 Pupils are now showing equivalence without images. Here they are given two fractions, and they need to determine what the first’s fraction top number is multiplied to get the second fraction’s top number. This is also done for the denominator. If they multiply the top and bottom by the same number then the fractions are equal, and they place an equal sign between the two. If the fractions are not multiplied by the same number then the fractions are not equal, and they place an not-equal sign between the two.
Pupils are now showing equivalence without images. Here they are given two fractions, and they need to determine what the first’s fraction top number is multiplied to get the second fraction’s top number. This is also done for the denominator. If they multiply the top and bottom by the same number then the fractions are equal, and they place an equal sign between the two. If the fractions are not multiplied by the same number then the fractions are not equal, and they place an not-equal sign between the two.
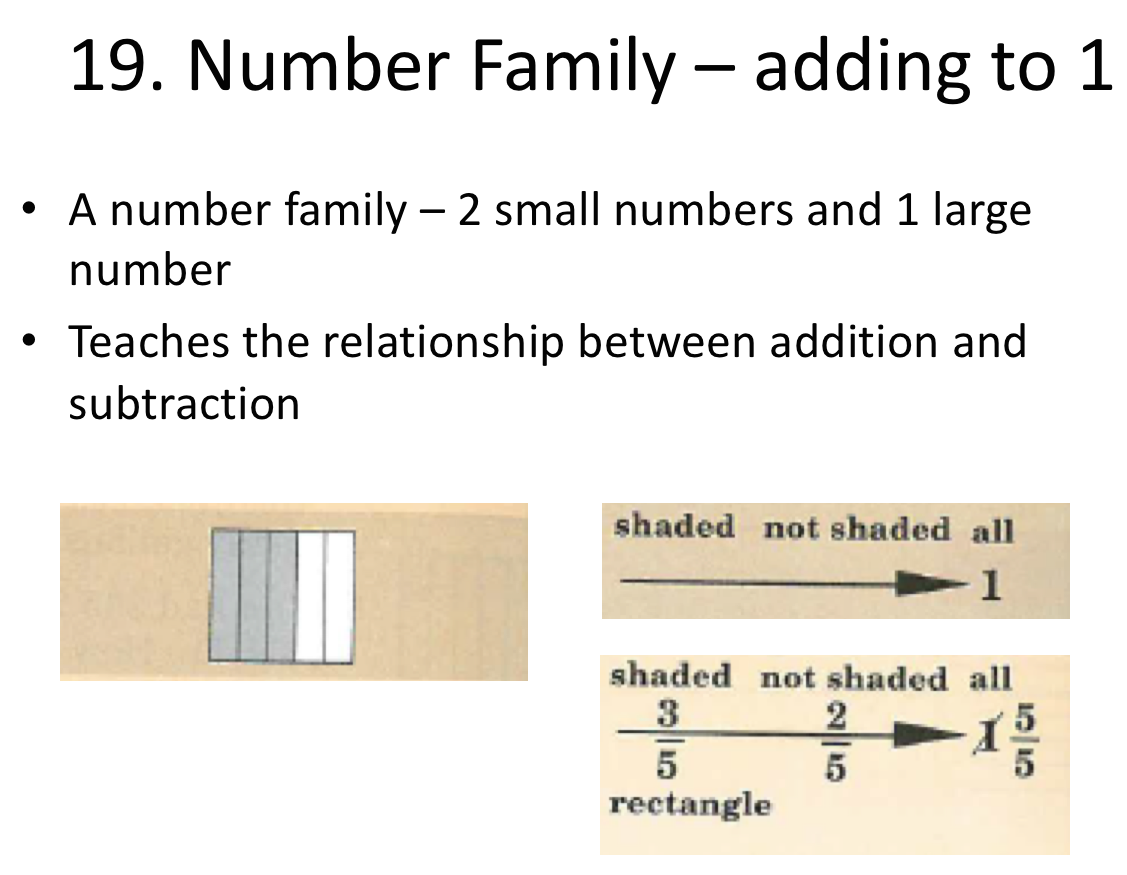
19. Number Family
A number family is a tool that pupils use to solve hard addition and subtraction problems. This has been blogged about here in a three-part series.
A number family is a sum between two small numbers presented above an arrow which has a large number at the end of the arrow. Pupils are taught that if you have a two small numbers then you add them to get the missing big numbers. Pupils are also taught that if you one big number and one small number then you subtract to get the missing small number.
Pupils are now taught how to apply this in problems where they need to demonstrate that the fraction of shaded parts and non shaded parts sum to 1.
On the number family, the fraction of shaded parts and the fraction of non shaded parts are the small numbers. They sum to 1, and pupils know this because they know that a fraction with the same top and bottom number simplifies to 1.
Exercises ask them to present a calculation between the shaded and non shaded parts.
Eventually pupils attempt exercises where they write a number family calculation from a sentence. They know that the number family’s big number will be 1. They write one as a fraction with the same denominator as the fraction of both small numbers.
This progresses in difficulty where pupils are given information not in terms of fractions but as whole numbers, they need to find the denominator and then write the information given as a fraction, then present in a number family structure.
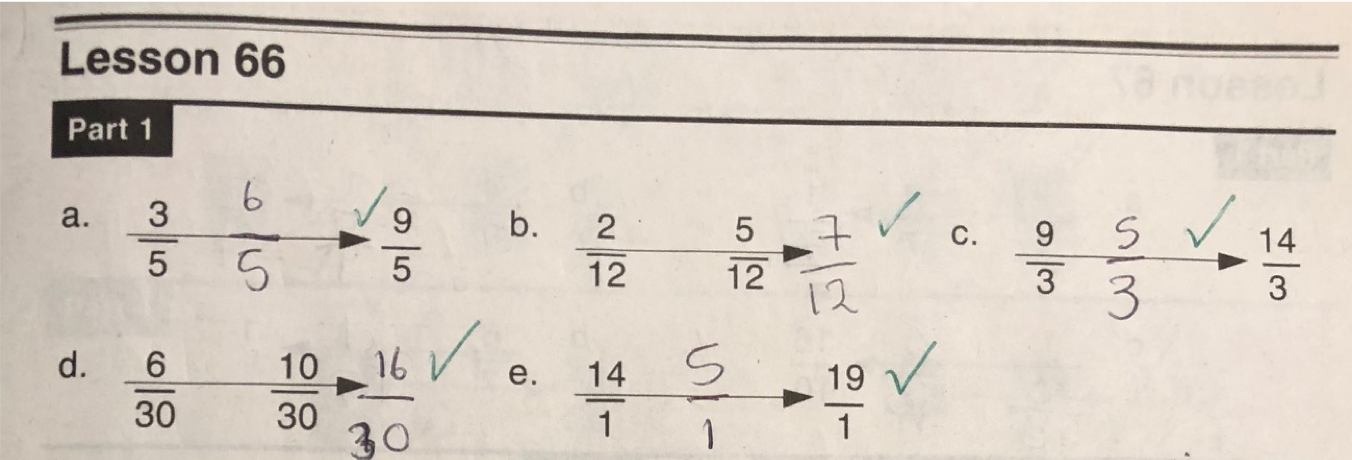
 Here are some examples of pupil work:
Here are some examples of pupil work:
20. Writing a mixed number as a decimal
The final component skill looks as getting pupils to write a decimal as a top heavy fraction and then as a sum of an integer and a proper fraction. Pupils are told that the decimal point is the plus sign between the integer and fraction. This was a very smooth transition from working with fractions to writing decimals.
What’s next…
After looking in great detail into Engelmann’s teaching, specifically with fractions, I’m now attempting to create exercises which can be used in the classroom for mainstream teaching. Watch this space!

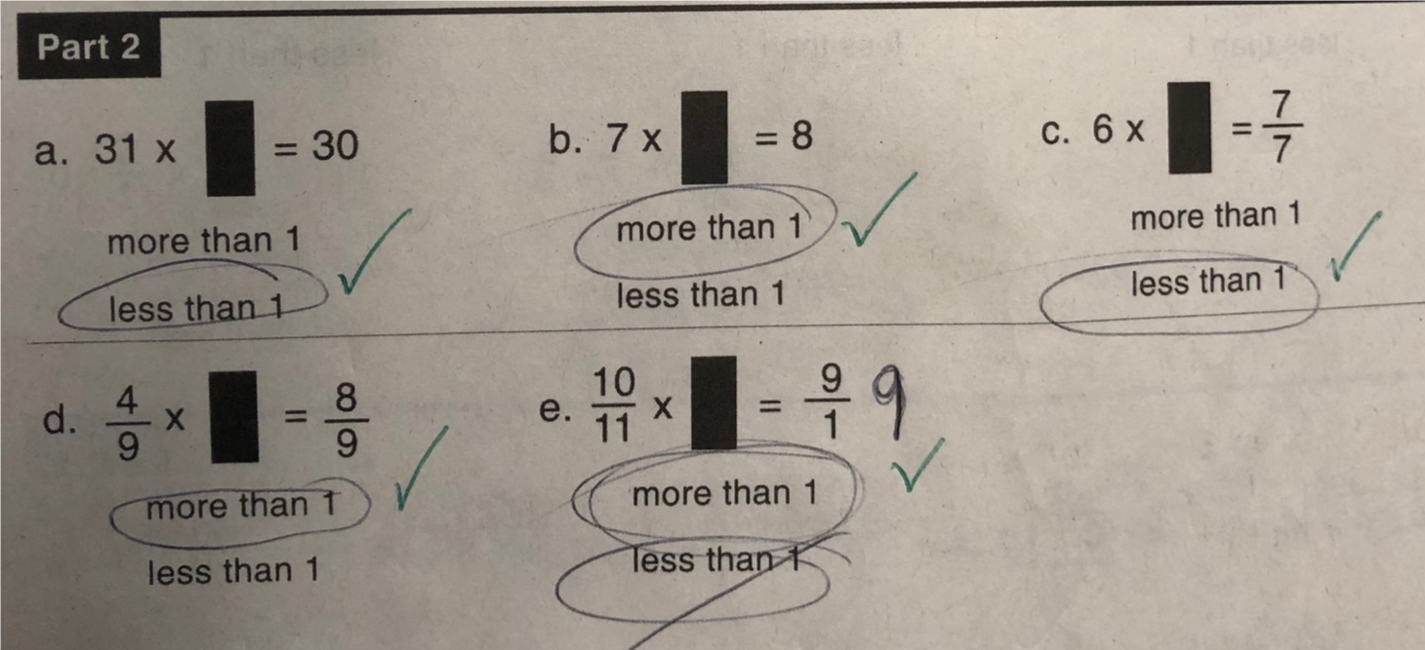


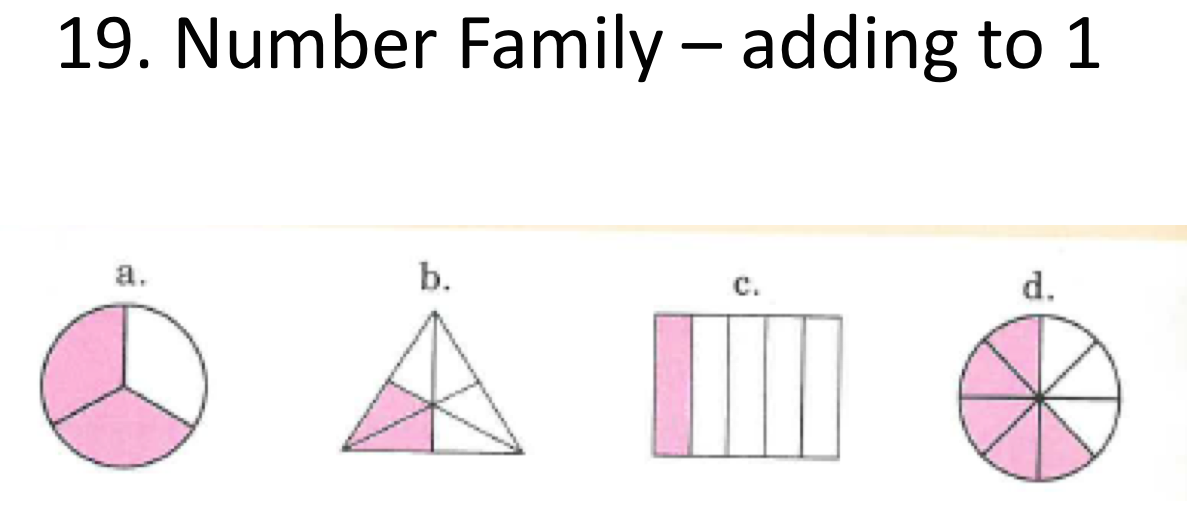




Recent Comments