During my second year at Michaela Community School, the department used Siegfried Engelmann’s Connecting Maths Concept Textbook series as the main teaching tool for Intervention. The textbook series comes with:
- A pupil textbook
- A pupil workbook
- Prepared Tests (after every 10 lessons)
- Teacher Presentation book
Each lesson would have:
- 4/5 Teacher-led exercises (using the presentation book)
- Independent pupil work
I know that some teachers would feel uncomfortable using a presentation book with prepared scripts but when I read through it I realised that Engelmann had written it better than anything else I had seen. The script is accurate, deliberate and is economical with text. This is something I will come to later on.
This blog post is one of a series to come. I will go through one specific skill that was taught and covered within the textbook and workbook for the pupils to really master. I will outline how this one specific skill was taught from the simplest problem type to the most difficult problem type. I will also show the same algorithmic set-up, as suggested by Engelmann in the Presentation book, which was used consistently when pupils worked through different problems which became increasingly more complex.
Here I will be looking at the relationship between addition and subtraction using something called a number family.
Here is the sequence of posts:
- Introducing the number family
- Manipulating the number family for complex worded problems
- Just when you thought the problems couldn’t get more difficult
- What is a number family?
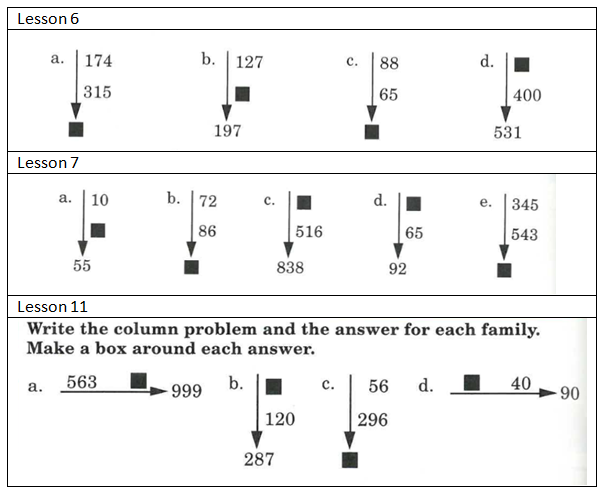
A lot of the addition and subtraction problems are based on using a number family.
A number family is made up of three numbers that always go together to make an addition and subtraction fact.
Engelmann introduces it as a family made up of two small numbers and a big number. The big number is at the end of the arrow. Here are the two facts taught:
To find the big number, you add the small numbers.
To find a missing small number, you subtract. You start with the big number and subtract the small number that is shown.
Engelmann also shows the two visual possibilities of the same problem. This explicit instruction within the presentation book is allowing pupils to develop a schema around the set-up they will be using to complete different addition and subtraction calculations. Engelmann is also pre-empting misconceptions which are most common by stating that “you start with the big number and subtract the small number that is shown.” How many instances have you seen pupils writing it in the reverse manner?
2) Deciding whether to add or subtract?
Engelmann states in the presentation book that the first question to ask pupils before they perform the calculations of the number family is: “Do we add or subtract?”
This is really valuable for pupils because they are being asked to decide what operation to use between the two numbers stated. They have to decide whether they have two small numbers or one big number and one small number. Through the number family it is also visually really clear for pupils to determine what combinations of numbers they have. Thus, helping pupils to see what operation to use.
Also, note that there are two and three-digit numbers included. This is to show pupils that we apply the same decision making question to calculations with digits of all size.
3) Number family where subtraction calculation requires no regrouping (#1)
The first few lessons pupils were asked:
“Do we add or subtract?”
“Write out the calculation from the number family.”
The subtraction facts did not include numbers that would require regrouping. Why? This is because subtraction which requires regrouping was a separate skill which was going to be taught within the sequence of lessons. This is really important! It is essential when you are teaching a pupil one specific skill at a time and also that you aren’t making it difficult for the wrong reasons. You are testing whether pupils can decipher which operation they need to use with the values given, not their subtraction skills with regrouping.
4) Number family where subtraction calculation does require regrouping (#2)
Once the subtraction with regrouping had been taught as a different skill then such subtraction calculations were included in the number family.
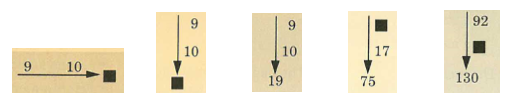
5) Visual variations of the same problem type
Engelmann introduces number families where the arrow is vertical. He shows that the calculation works the same even if the arrow was horizontal. Visual variations of the same problem type show pupils that some changes are irrelevant. The set up with a vertical or horizontal arrow does not change:
- The question we ask whether to “add or subtract”
- Which is the big number or small number because the big number is always at the end of the arrow. Small numbers are always along the arrow.
To then include questions sets of the similar type:
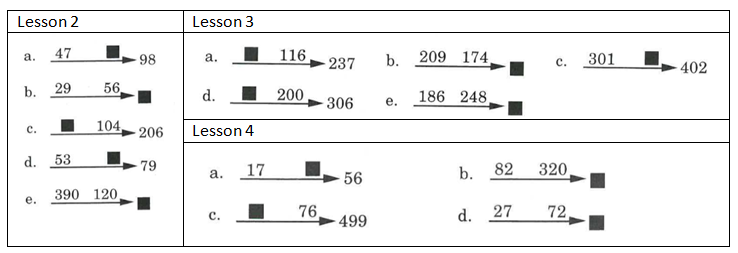
This has now been taught explicitly by the teacher using the presentation book. From lesson 11 this skill is practised within the Independent task section of future lessons to ensure pupils don’t forget what they have learnt. Below, I have a table listing the amount of lessons where horizontal and vertical number families are present, in which lessons and in what capacity:
Blue = Teacher-led exercise using prepared script + teacher-guided qus
Green = Independent task where pupils are being tested
White = not present in the teacher-led exercise or independent task
Each number represents the Lesson no. E.g 6 = Lesson 6
In the next post, I will go into the complex worded problems pupil were able to attempt and accurately complete by manipulating the number family set-up.



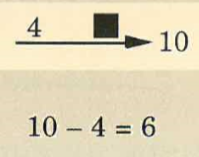
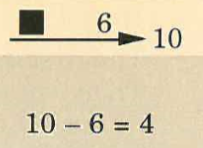



Leave a Reply
You must be logged in to post a comment.