This post will be outlining the academic rigour I have seen in the teaching and in the assessments created by the Uncommon Schools Network. I shall explain how we can develop such rigour in our classrooms as individual teachers.
Each grade (year group) has an interim assessment exam which is determined centrally by a subject lead teacher; although collaboratively made, a subject lead teacher will finalise the exam produced. Once it is finalised, all teachers within the network will have access to view the assessment but will not have the access to make any amendments/alterations.
I was very impressed by the interim assessments made, because they are created in a way in which pupils’ mathematical knowledge is tested in a manner where they are forced to manipulate the knowledge they have: it tests and masters the fine balance between procedural fluency and conceptual understanding in each question. It also made me reconsider how I plan my teaching, how I now combine concepts in different problem types and how I try to make rigourous low-stake quizzes including questions like the ones you are about to see.
I am going to look at one question which I thought was brilliant, then explain how I would plan a selection of lessons, in a sequence, inducing pupils to become mathematically proficient and confident in order to attempt such a question.
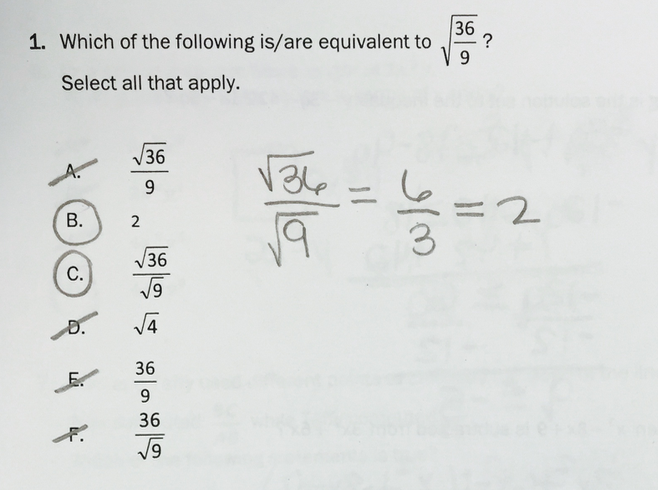
Here I am assuming by convention from how I was trained and from what I have seen in my experience, previously I would begin by teaching the concept of square numbers and square roots, by getting children to identify the square numbers by multiplying the root number by itself, and then drawing the link: that once you square root a square number you will obtain the initial root number which, multiplied by itself, then results in that square number.
Then, I would have possibly explored completing calculations with square numbers and square roots. After that, in years to come, I would teach square numbers and square rooting in relation to fractional indices and with surds. When teaching surds, I would bring in the idea of rational and irrational numbers. Here is what I now suggest!
This is how I would map out teaching the topic of square numbers, square roots and holding a root number, to an index number greater than 2, and introducing rooting greater than a square root. Kids must have gotten to a stage where such calculations are memorised:
Why not bring in the idea of interleaving fractions, decimals etc?
Then, I would build upon the previous questions systematically, in a way in which students can create a fraction which can be simplified.
Also, I would introduce from an early stage the proposition that when we square root a square number we get positive and negative of the root number, which can be a really valuable discussion to have with children. Introduce calculations afterwards with square numbers and square rooting. This type of thinking is driven by another question I saw in a North Start Academy assessment:
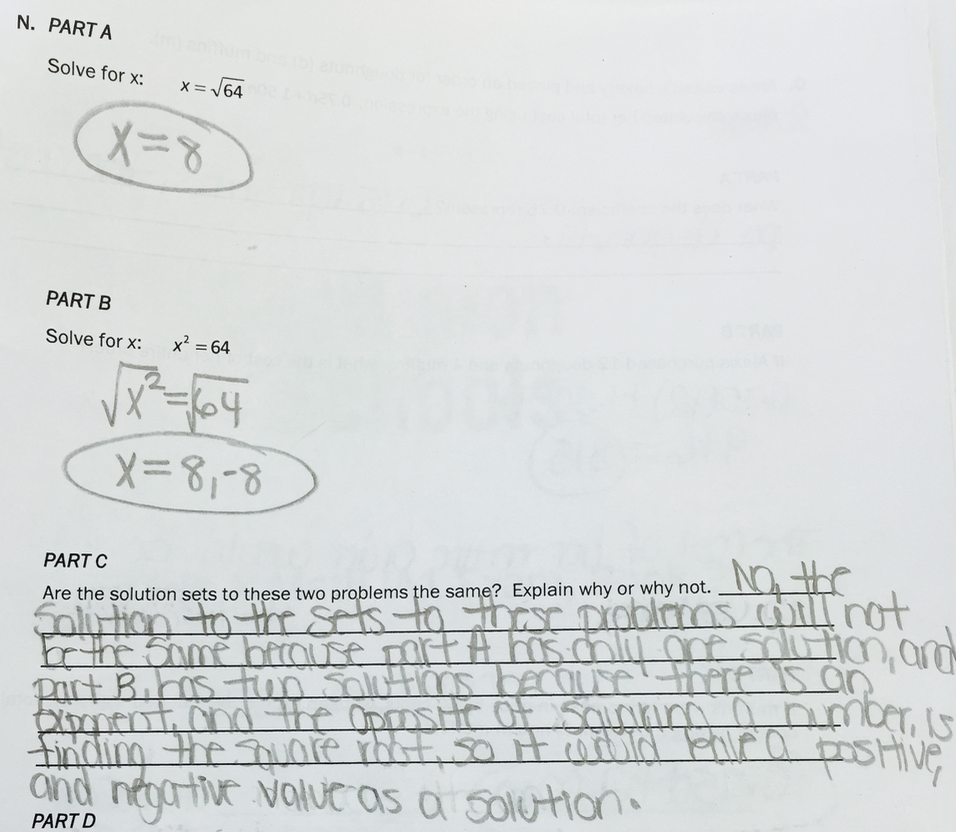
The question is touching on key knowledge that when x is equal to a square root then we assume a positive value as an answer, however when x is held to an exponent the values of x will result in a positive and negative value.
Eventually I would introduce a base number to an exponent greater than 2 and interleave it into calculations:
I could get pupils to then go into the following questions:
Or, have pupils determine the value of unknowns through trial and error:
Now, I am going to draw a link between square numbers, square roots and rational numbers without linking it to fractional indices and surds. The purpose behind this is to (for now) restrict what I would teach at Year 8 or 9 but, at the same time, providing that conceptual scope. Simultaneously, it also provides the opportunity for multiple choice questions that have the academic rigour for our pupils.
I would define a rational number and then go into the necessary vocabulary such as ‘a rational number is a number which can be written as a fraction of two integers. A rational number cannot be written as a non-repeating or non-terminating decimal’, for example, in comparison to 0.45454545 which is a rational number. I would then provide a selection of example and non-examples.
I could test children’s understanding through mini whiteboards or hands up: 1 if it is a rational number and 2 if it is an irrational number; selecting the order of questions such as 2, 6, 100, 15, 1/2 , 5/6, 10/100, then bringing in the square numbers and asking pupils to show why it is a rational number or irrational number such as √16, √36 or √144
Pupils could type in the value of √12 or √3 in a calculator to see that you will get a non-repeating or non-terminating decimal that cannot be written as a fraction of two integers therefore categorising such non examples as irrational numbers.
Also then mentioning that square rooting a square number will result in a rational number, and cube rooting a cube number will result in a rational number etc.
You would then be able to explore the idea of rational numbers in which you are square rooting square numbers using your calculator:
Following this, discussion will be made of the notion that the following are rational numbers in regard to the definition of a rational number being a number that can be written as a fraction made of two integers:
Then, the idea of either the numerator or denominator being a whole number should be brought into my teaching:
 After that, I would introduce problem types where you can simplify the fraction:
After that, I would introduce problem types where you can simplify the fraction:
Discuss that the problem below results in an irrational number because the numerator is irrational and overall the solution cannot be written as a fraction of two integers:
Will the following number sentences produce rational numbers?
Children need to be comfortable in identifying that is not a rational number because it cannot be displayed as a fraction of two integers. The definitions need to be consistent so that children are confident in differentiating between a rational and irrational number using square numbers and square roots, and then moving onto powers greater than 2. If we expose children to the following above we are providing the academic rigour which future exam boards are attempting to build upon.
All of this is just an idea which I am trying to explore in order to provide students with the academic rigour, in terms of their classwork and in the assessments, that they will be taking.

Everything that I have written, the problem types I have created and the interconnections between square numbers, square rooting, and rational numbers, is a result of looking at such questions above. These questions guided me to plan a selection of lessons which provide the balance between enabling students to become procedurally fluent in calculations and in developing conceptual understanding of this topic.
Through creating difficult assessments you can guide your teaching to induce that academic rigour. I have never taught maths like this, but I do plan to in the future. This was all inspired through looking at this question at North Star Academy in New Jersey. The academic rigour present in the interim assessment guides to create academic rigour in what is being taught and learnt within the classroom.
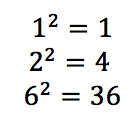
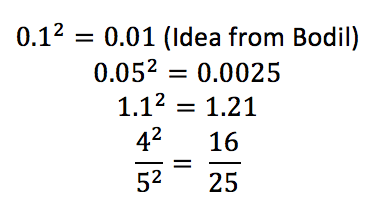
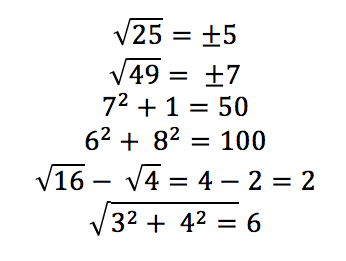
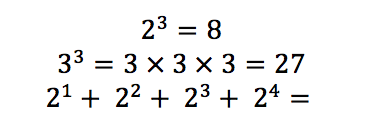
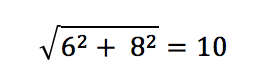
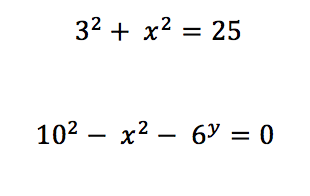
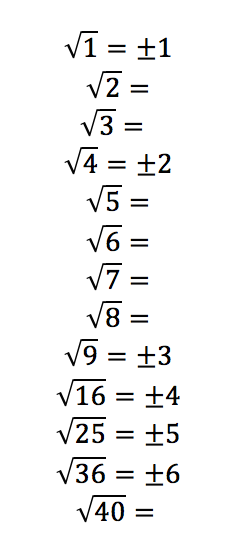
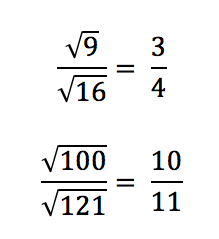
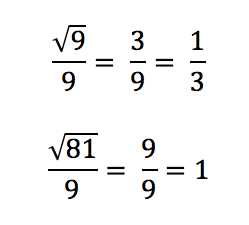
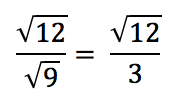
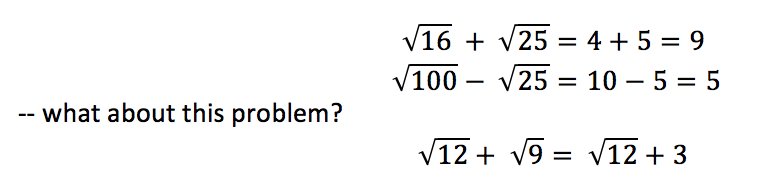



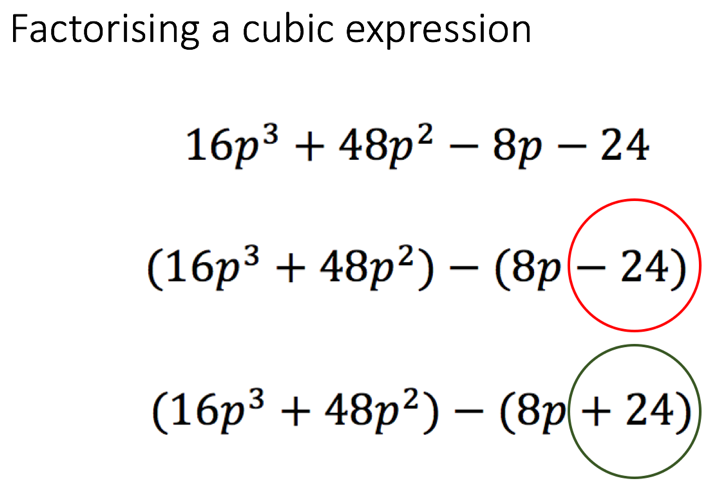
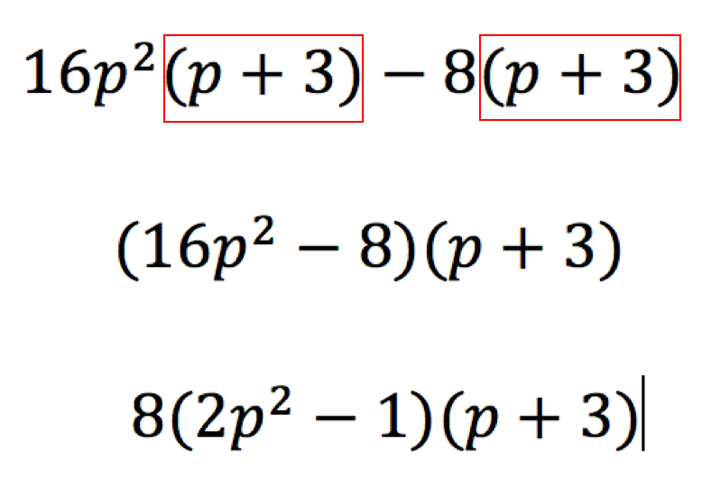
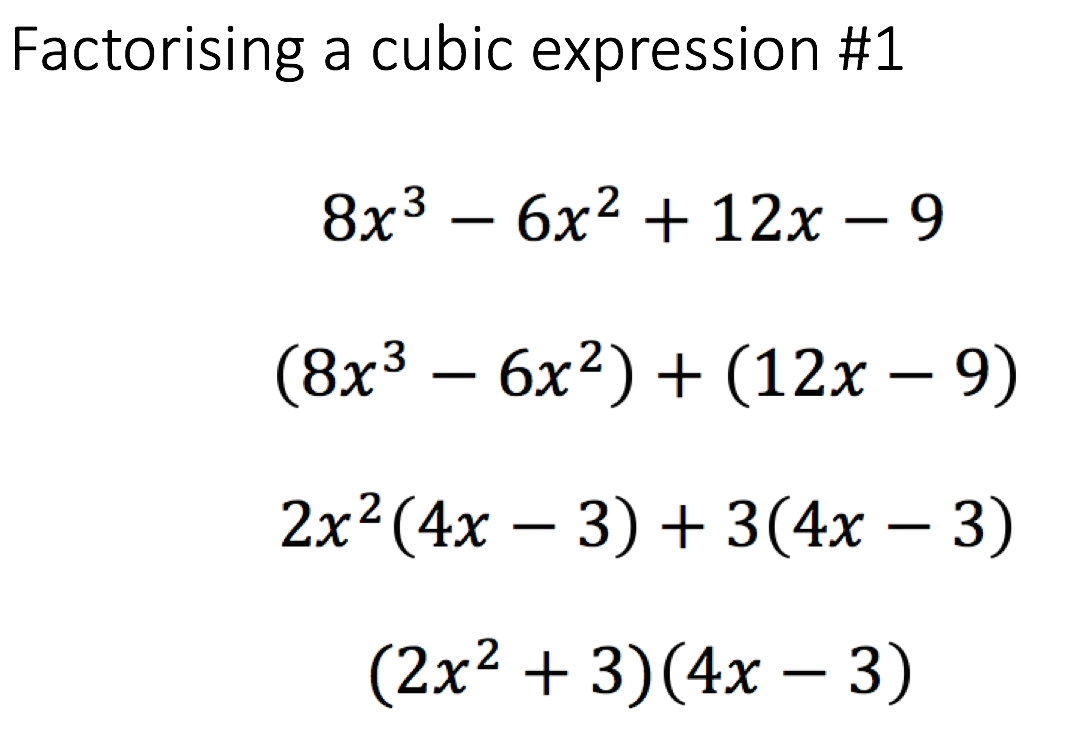

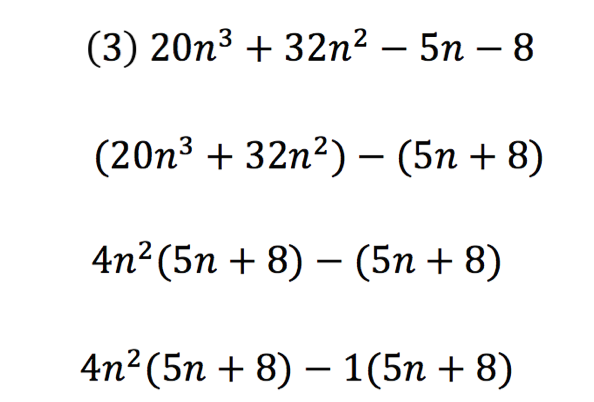
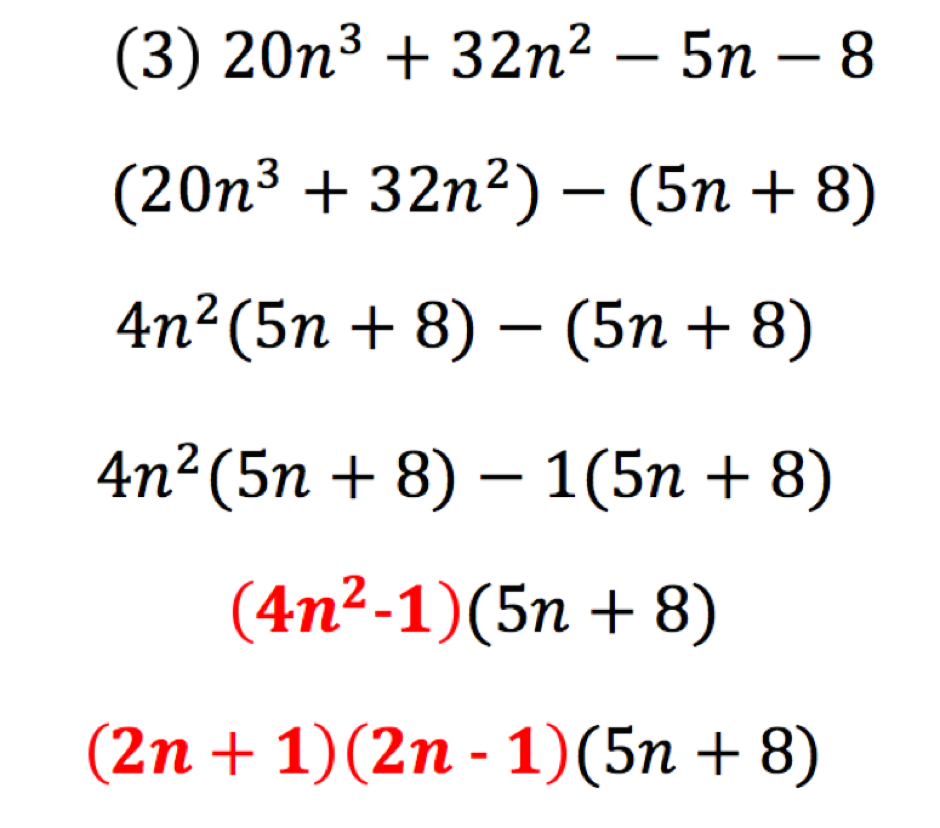


Recent Comments