Despite being a secondary teacher, I’m inspired to move into primary. The scope for determining a child’s academic trajectory from their primary education is huge. Beyond my imagination. And the more I learn about primary education, focusing on primary mathematics the more inspired I am to visit Primary schools.
I had the pleasure of meeting Terri Leighton, Principal of Dixons Manningham, whilst attending the National Institute for Direct Instruction conference. We both attended the Administration (Principal) Institute to learn about the most ideal conditions for a primary school running Direct Instruction (DI) Programmes. The Institute covered everything from the DI programmes to run from Reception to Year 6, scheduling, teacher recruitment, coaching and data collection. It was the best CPD I’ve ever had, and I regularly refer to my notes from the conference.

I arranged a visit to Dixon’s Manningham in Bradford which was kindly arranged by Abigail Burrows (Class Teacher). It was eye-opening and debunked some of the false narratives I’ve heard about primary education. My two takeaways were (a) consistency in routines and (b) Modelled Direct Instruction
Before I begin, I saw very happy, enthusiastic and successful children. I saw committed and happy teachers who knew they were making a difference. For that reason alone, I’d recommend visiting. I also loved seeing Family lunch in a primary context.
Consistency in Routines
In the space of a day, I visited every single classroom and watched a lesson from every year group. The consistency of routines was evident across the school from Early Years to Year 6. I saw consistency in teacher language for a specific desired pupil change in behaviour to prepare for the next teaching activity. And this was the case across each room I went to observe. For example,
Teacher: 3-2-1-Eyes on me
Pupils: 3-2-1-Eyes on you (all in sync)
The teacher would change their posture to model to children that they need to empty their hands, cross their arms, turn their bodies to face the teacher, and sit tall in their chairs. I saw the use of timers for ‘Watch the clock’, ‘Cold Call’ to see pupils all engaged and actively listening. I saw the use of ‘No Opt Out’ to ensure that a pupil who couldn’t participate had an opportunity to later.
Routines were embedded in ways which were noticeable and unspoken. This shows that the teachers hold pupils to account to follow through with the routines because pupils knew what to do. For a school to achieve this, school leaders and teachers sweat the small stuff. I’ve seen it executed well during my time at Michaela Community School and Great Yarmouth Charter Academy. Here are some examples of the routines I saw at the school:
- Pupils had their equipment positioned the same way in each classroom.
- Pupils knew how to begin the Do Now with minimal teacher instruction. This ensured a purposeful start to the lesson.
- Pupils walked around the school in a single file. I saw teachers in Early Years and Year 1 stating the expectations for lining up, entering the classroom and exiting. Hands by your side, eyes facing forward and tracking me.
- Pupils had a school planner where they diarised their assigned homework, reading records etc.

When I asked Terri about the systems behind the consistency in routines, she explained it’s twofold:
- Weekly coaching meetings between colleagues
- Planned Coaching strand
The planned coaching strand was insightful. It gave structure and guidance to the coaching sessions. The school identified the 6 non-negotiable TLAC (Teach Like a Champion) techniques that provide a purposeful, pacey and positive teaching environment. Each coach works with their assigned teachers to rehearse and implement a new TLAC technique. The strand allows flexibility to focus and master implementing one TLAC technique or move on to mastering more. See the image below.
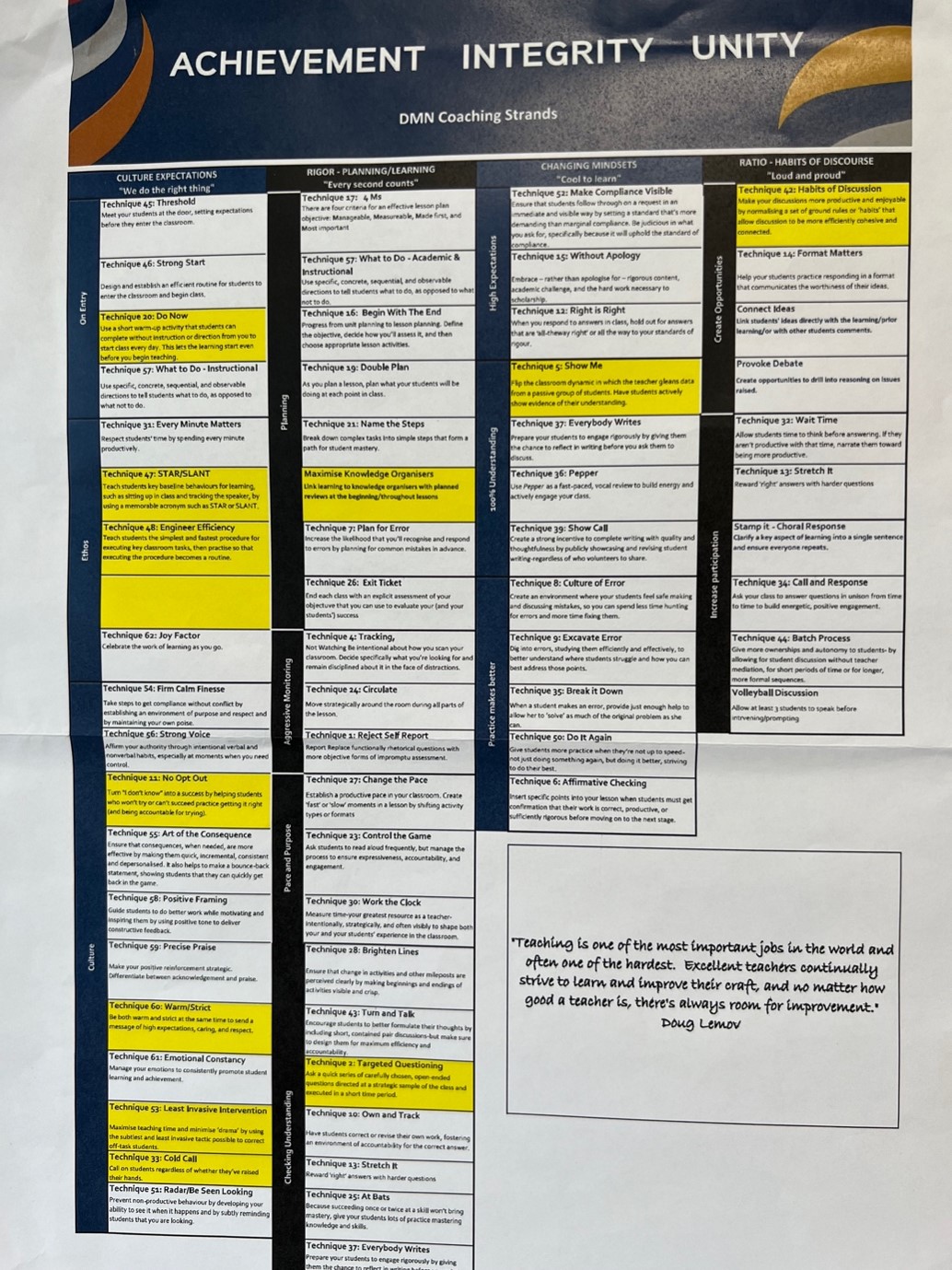
Modelled Direct Instruction
I visited Dixons Manningham to watch DI programmes implemented in a primary setting. I saw a range of different programmes but here were the main takeaways:
- The classroom was set up, so pupils were visible to the teacher, and the teacher was visible to the pupils.
- Pupils had the relevant textbook/worksheet during instruction, and all had their index fingers at the correct part and followed the teacher’s instructions
- Pupils were moving through the content at pace
- When pupils made a mistake, the teacher took them through the seven steps of error correction. See image. This meant that when a child made a mistake it was corrected before moving on. This is a key element in DI teaching.
- Pupils were answering the teacher on signal and in sync

This is what I saw from the teachers:
- Teachers projected their voice to ensure that pupils responded with answers loudly and clearly
- Teachers signalled to pupils when they wanted pupils to respond e.g., by moving their hand
- The teachers were all enthusiastic and present. They had children gripped to every word.
- Teachers were scanning the room to ensure that pupils were tracking, listening and participating. Stopping in their tracks when a pupil began to fiddle or look out the window
It’s difficult to understand how DI Programmes are taught unless you’ve had pre-service training from NIFDI, taught a programme or watched DI lessons. Will potentially write a bit more on this soon.


I’m excited to watch Dixons Manningham’s journey. A statistic they shared with me: 71% of pupils in Year 3 are meeting age-related expectations. Expected to be higher for the next cohort of Year 3s. This is promising given that in 2019, 65% of pupils reached the expected standard in reading, writing and maths (combined).
 I’m incredibly passionate about one school, Ernulf Academy in St Neots, and we are searching for a Head of Maths.
I’m incredibly passionate about one school, Ernulf Academy in St Neots, and we are searching for a Head of Maths. The anecdotes to choose from are many, but I here are a few. One member of staff inquired if I’d be teaching any lessons for him so he could observe. I wasn’t, but I offered to teach his next lesson for him to watch. I emailed the Department, and three members also joined in observing. This was possible because of our systems. Next section.
The anecdotes to choose from are many, but I here are a few. One member of staff inquired if I’d be teaching any lessons for him so he could observe. I wasn’t, but I offered to teach his next lesson for him to watch. I emailed the Department, and three members also joined in observing. This was possible because of our systems. Next section.

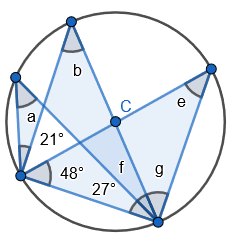
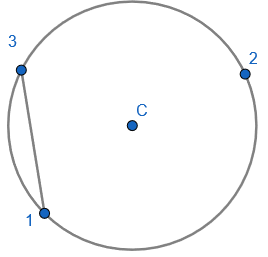
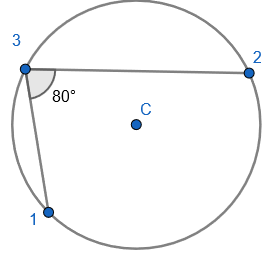
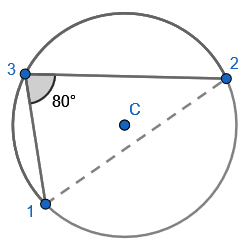
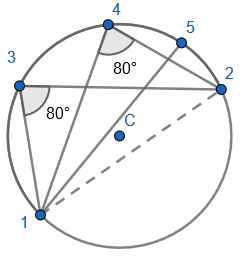
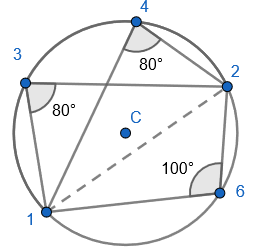
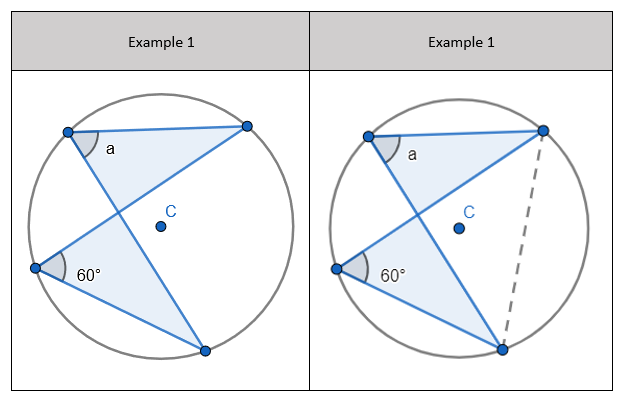
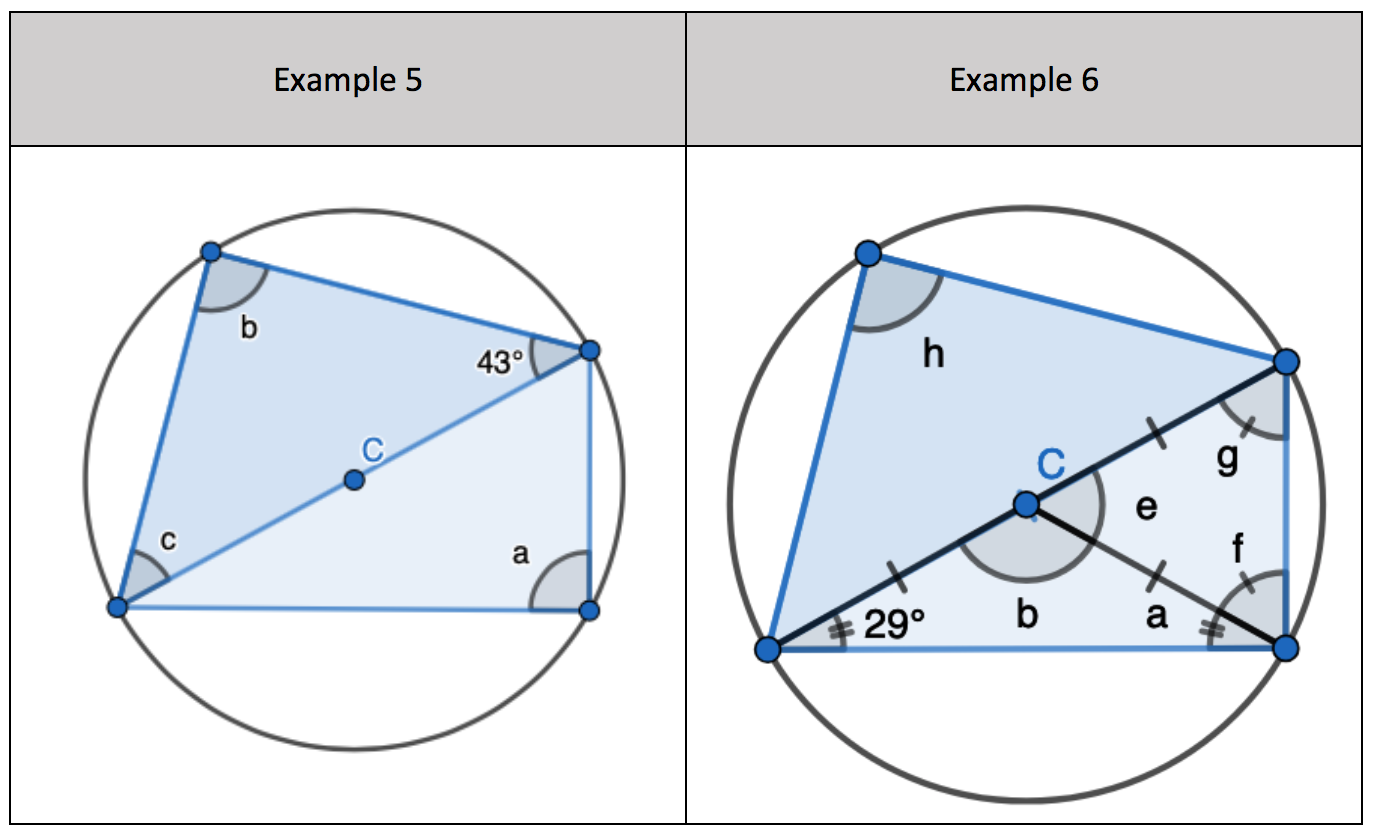
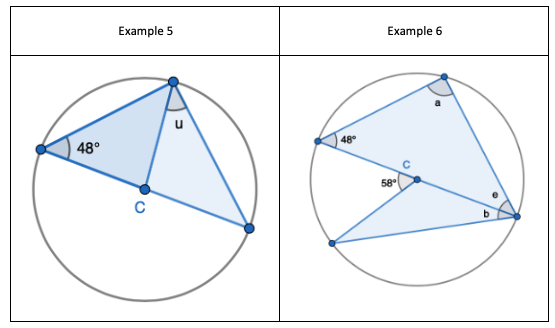
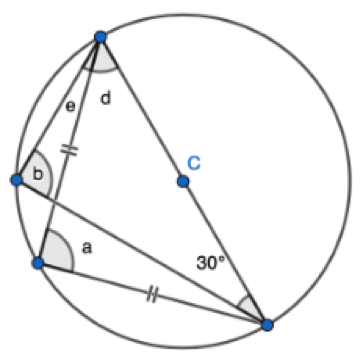
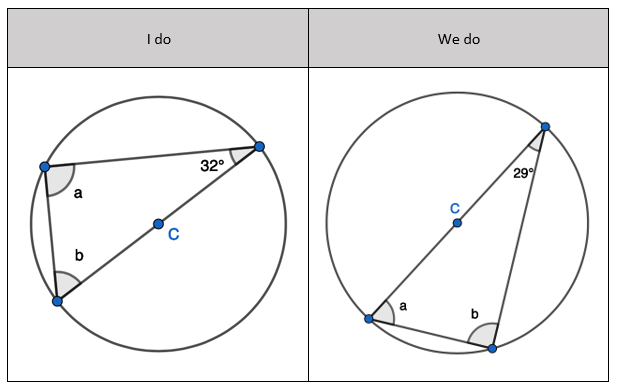
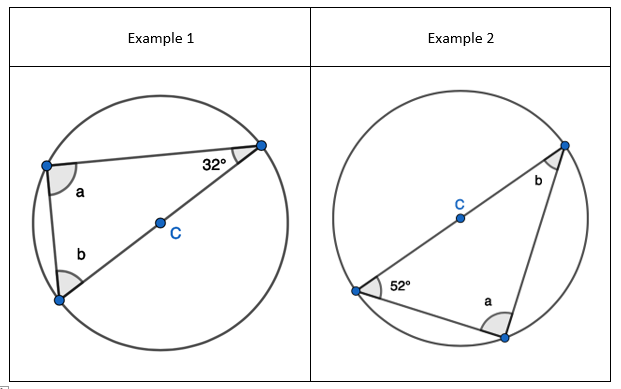
 2. State that angle ‘a’ and ‘b” is 60 degrees because the angles at the circumference are equal in the same segment. Here we are showing that more than two angles are equal in size at the circumference from being in the same segment. I have interleaved the first circle theorem – an angle in a semi-circle is 90 degrees. If we total ‘b’ and 90 degrees to then subtract from 180 degrees then we can find ‘e’.
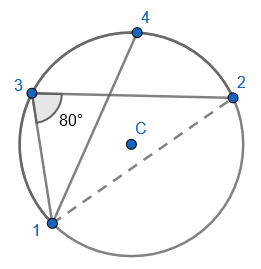
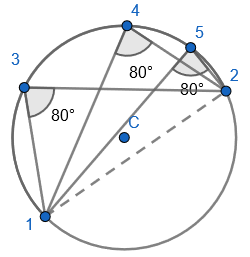
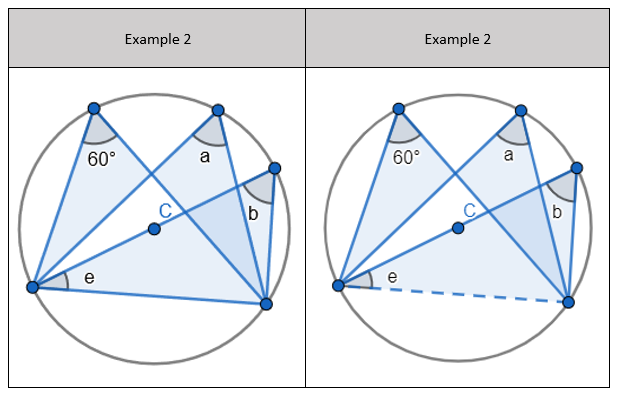
2. State that angle ‘a’ and ‘b” is 60 degrees because the angles at the circumference are equal in the same segment. Here we are showing that more than two angles are equal in size at the circumference from being in the same segment. I have interleaved the first circle theorem – an angle in a semi-circle is 90 degrees. If we total ‘b’ and 90 degrees to then subtract from 180 degrees then we can find ‘e’.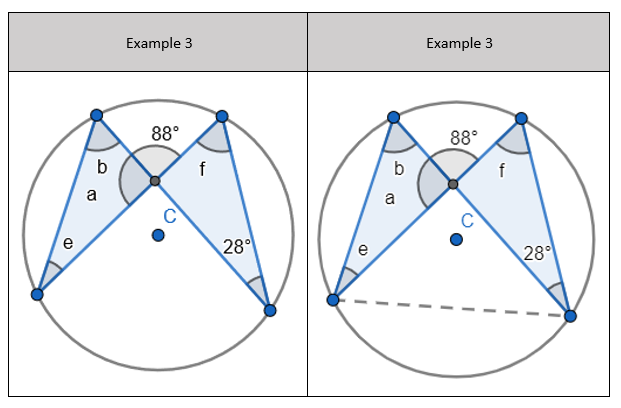 3. State that angle ‘e’ is 28 degrees because the angles at the circumference in the same segment are equal. Find ‘a’ using the basic angle fact that angles on a straight-line sum to 180 degrees. Find ‘b’ using the basic angle fact that angles in a triangle sum to 180 degrees. State that ‘f’ is the same angle size as ‘b’ because of the circle theorem we have just learnt.
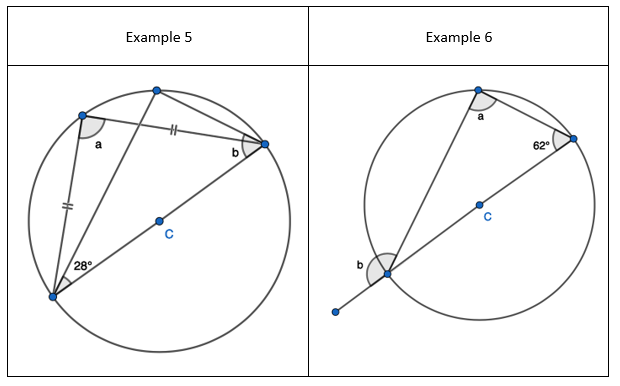
3. State that angle ‘e’ is 28 degrees because the angles at the circumference in the same segment are equal. Find ‘a’ using the basic angle fact that angles on a straight-line sum to 180 degrees. Find ‘b’ using the basic angle fact that angles in a triangle sum to 180 degrees. State that ‘f’ is the same angle size as ‘b’ because of the circle theorem we have just learnt.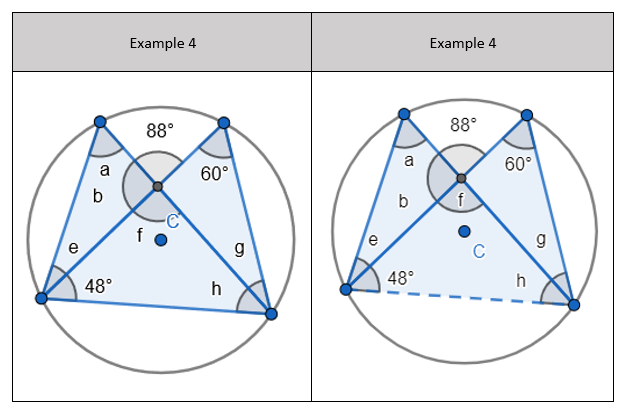
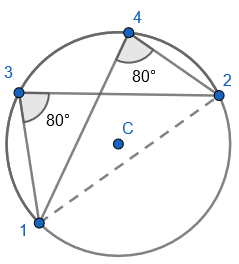
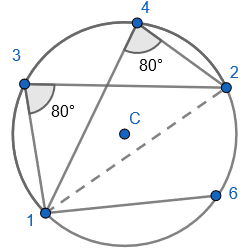
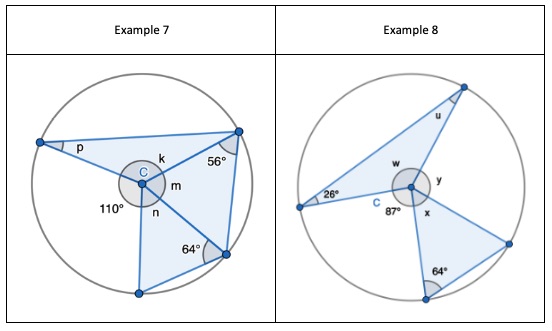
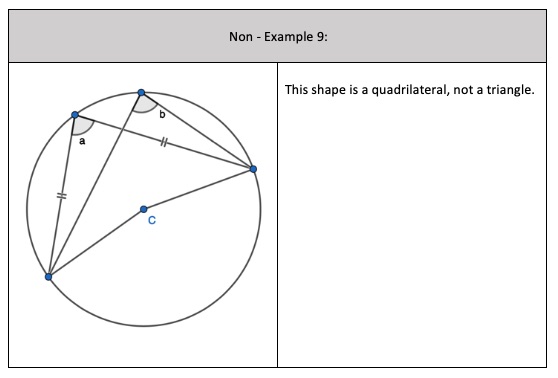
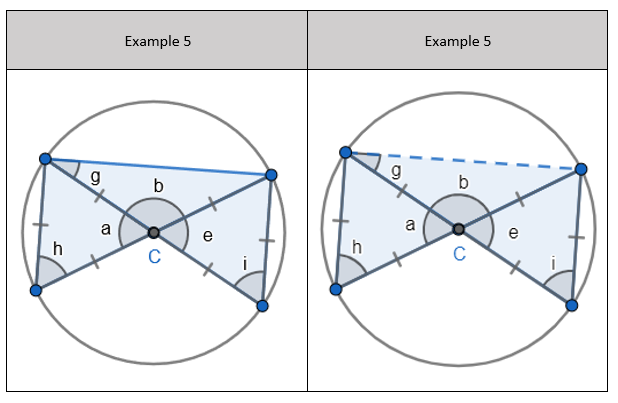 5. Pupils can see that there are two equilateral triangles meaning ‘a’, ‘h’, ‘e’ and ‘I’ are all 60 degrees. I would mention that angle ‘h’ and ‘I’ are equal because those angles at the circumference are in the same segment.
5. Pupils can see that there are two equilateral triangles meaning ‘a’, ‘h’, ‘e’ and ‘I’ are all 60 degrees. I would mention that angle ‘h’ and ‘I’ are equal because those angles at the circumference are in the same segment.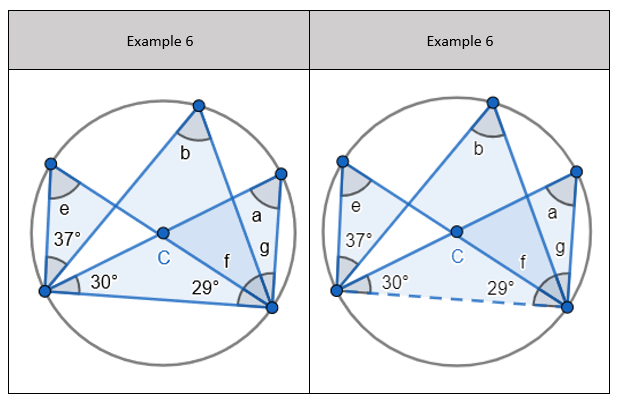

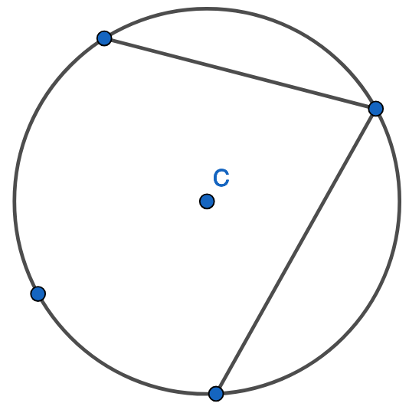
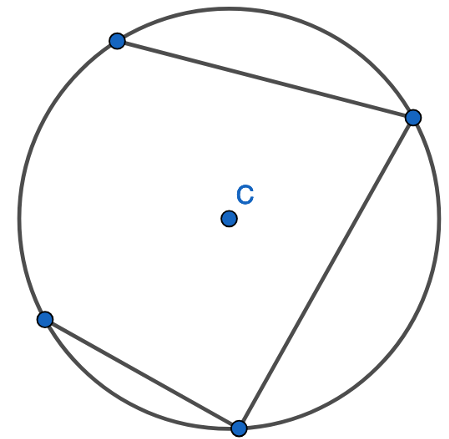
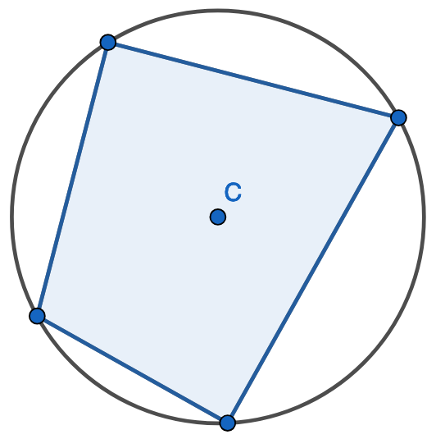
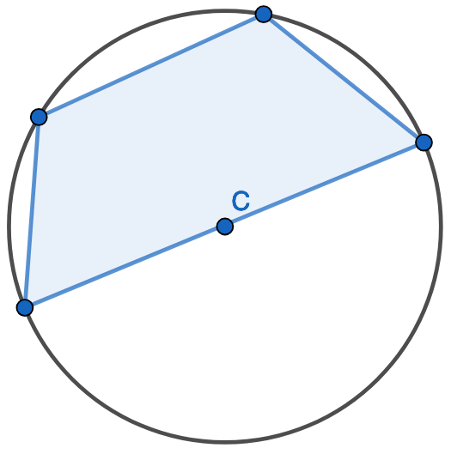
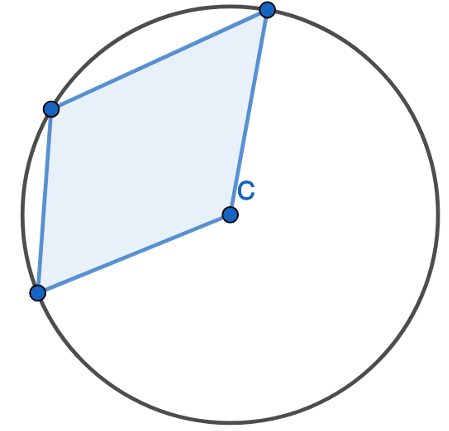
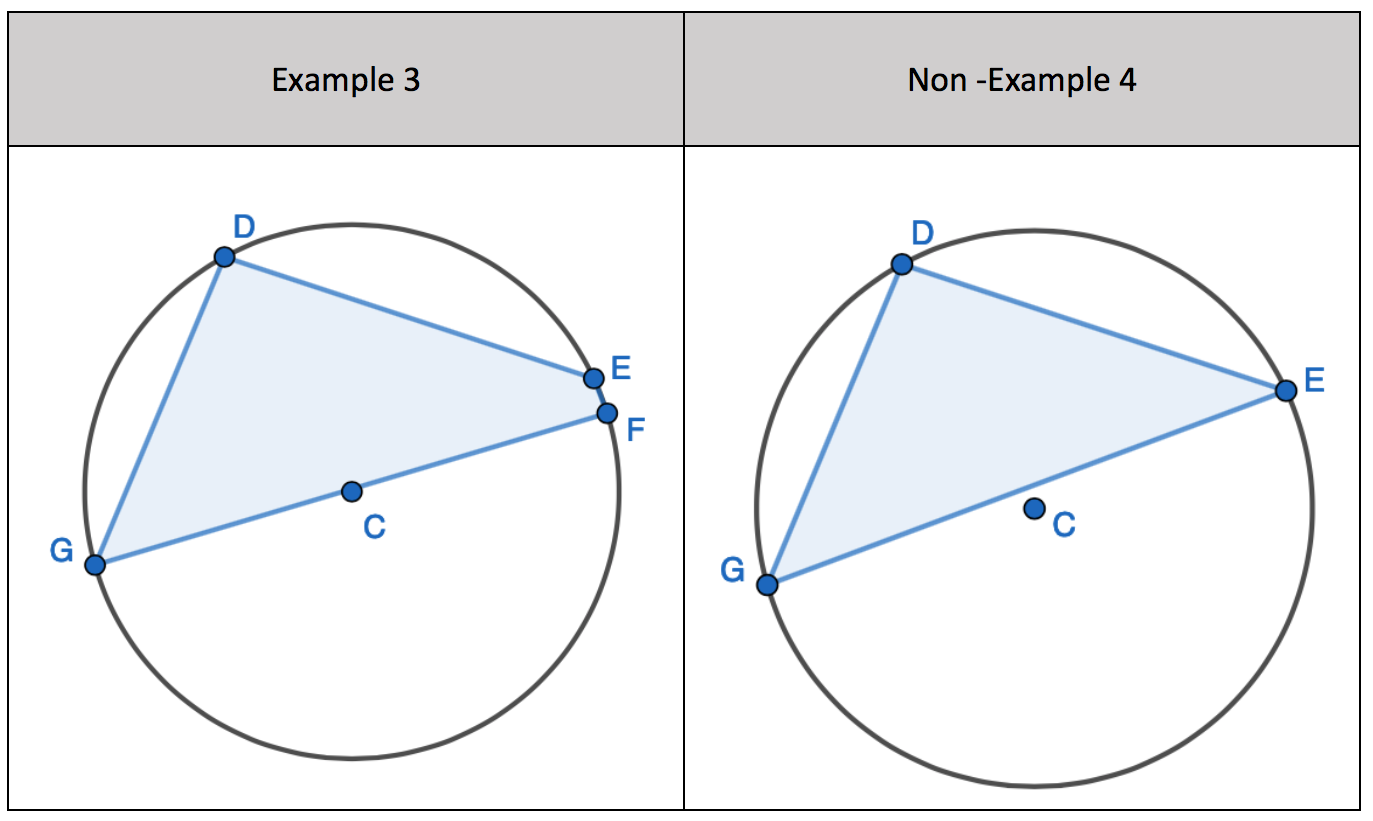
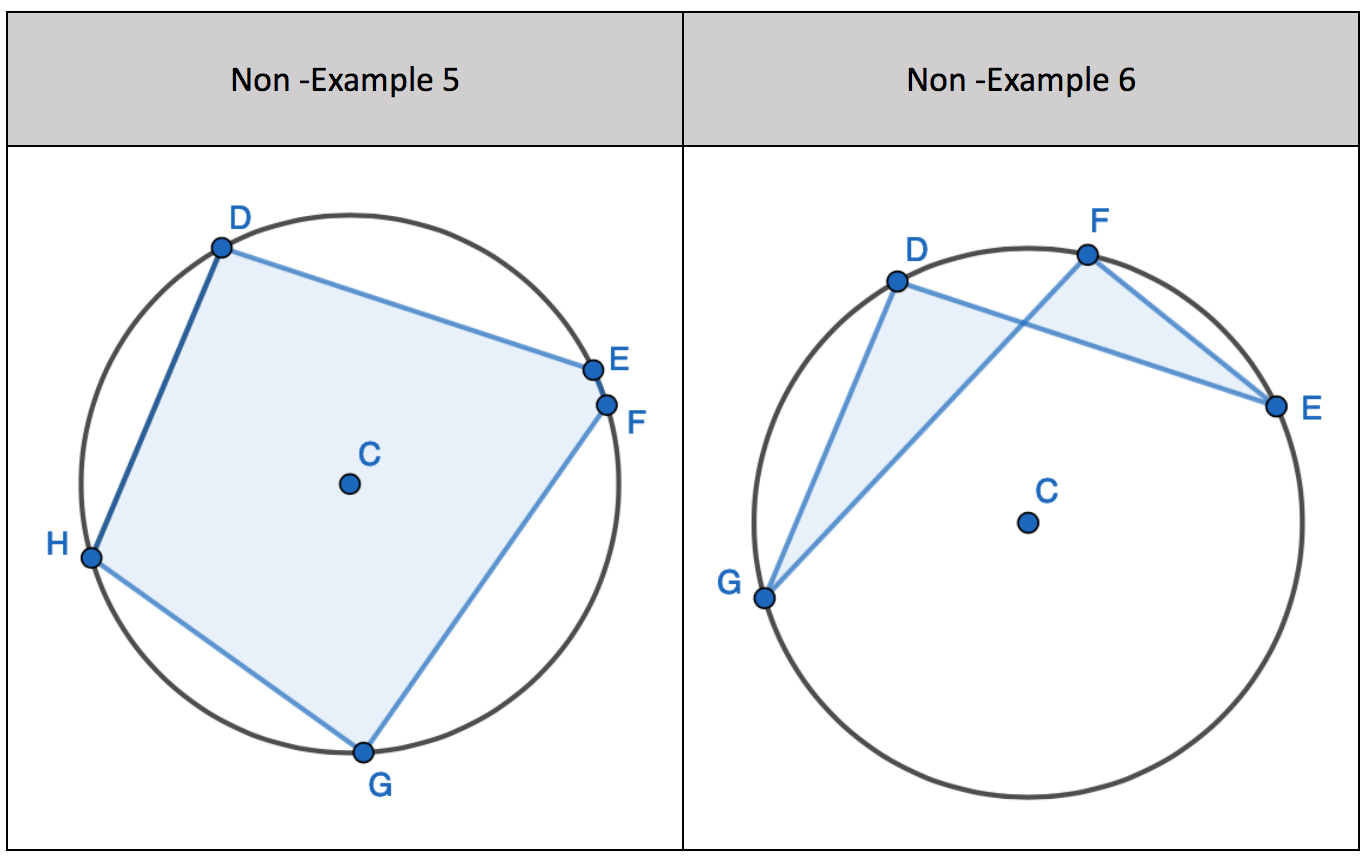
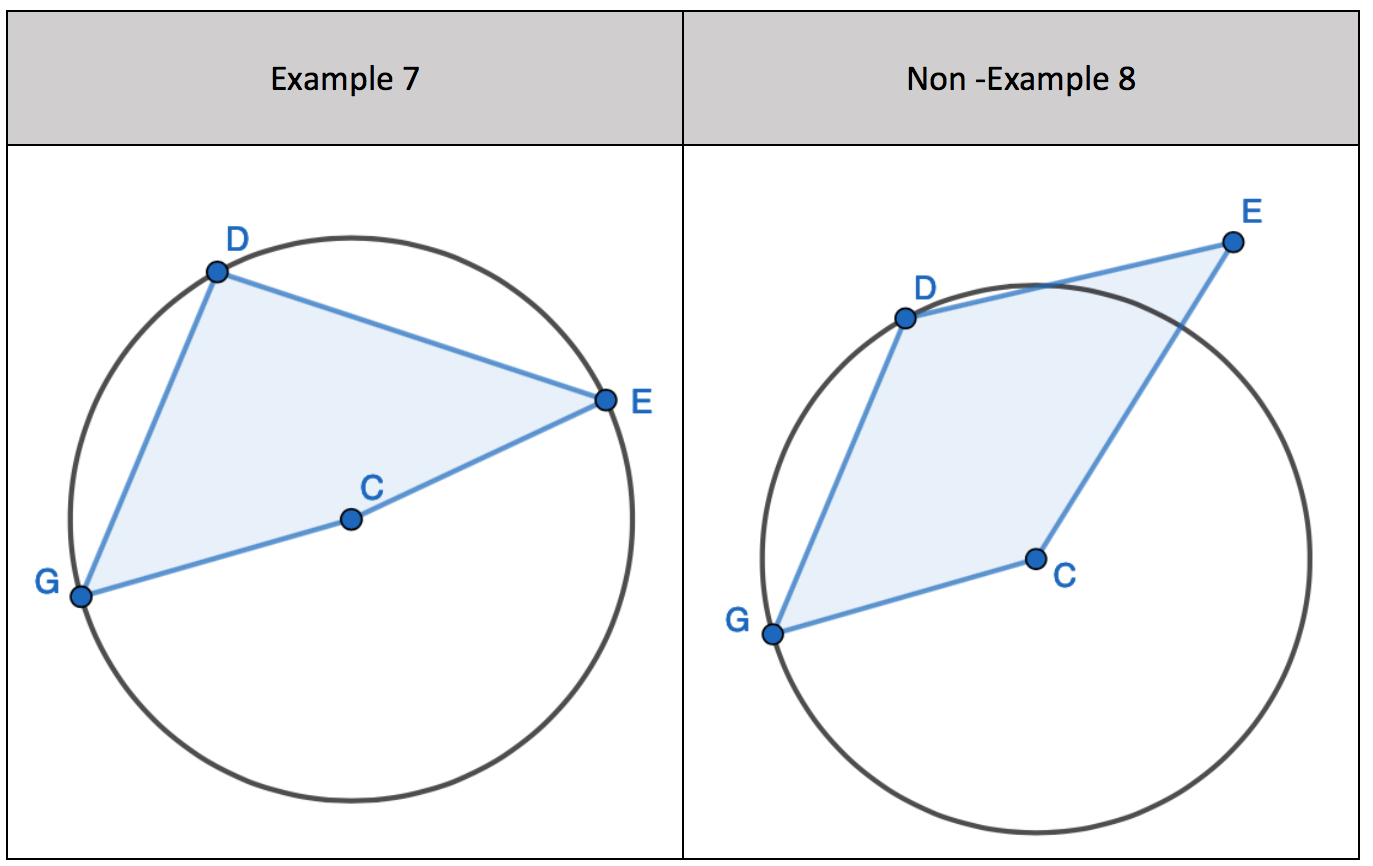
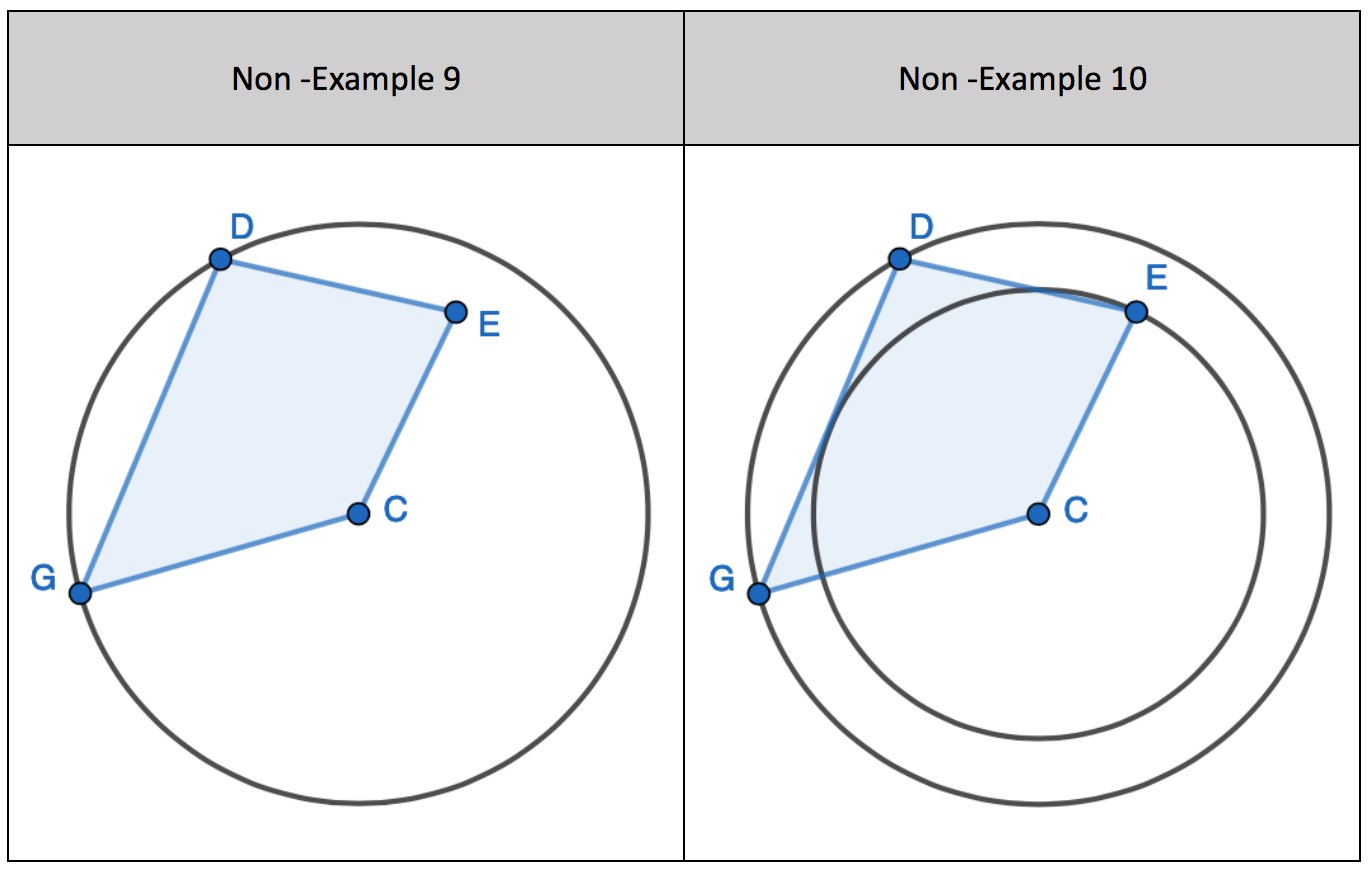
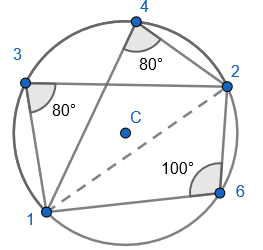
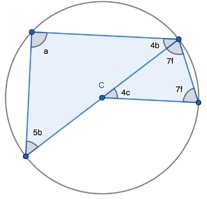
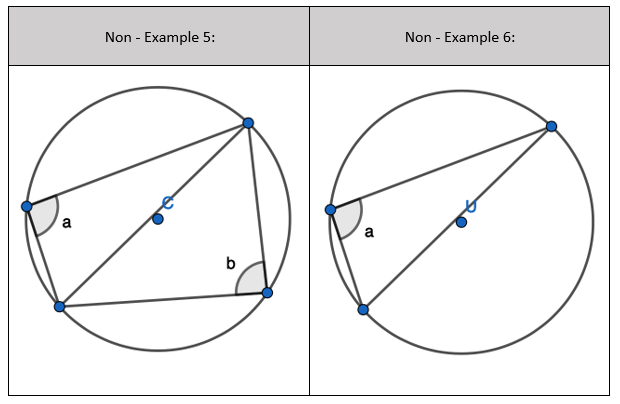
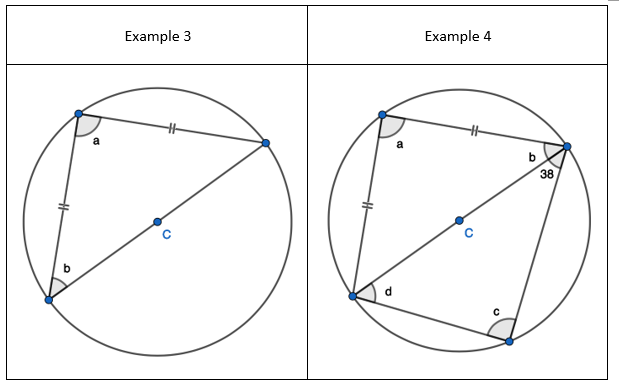
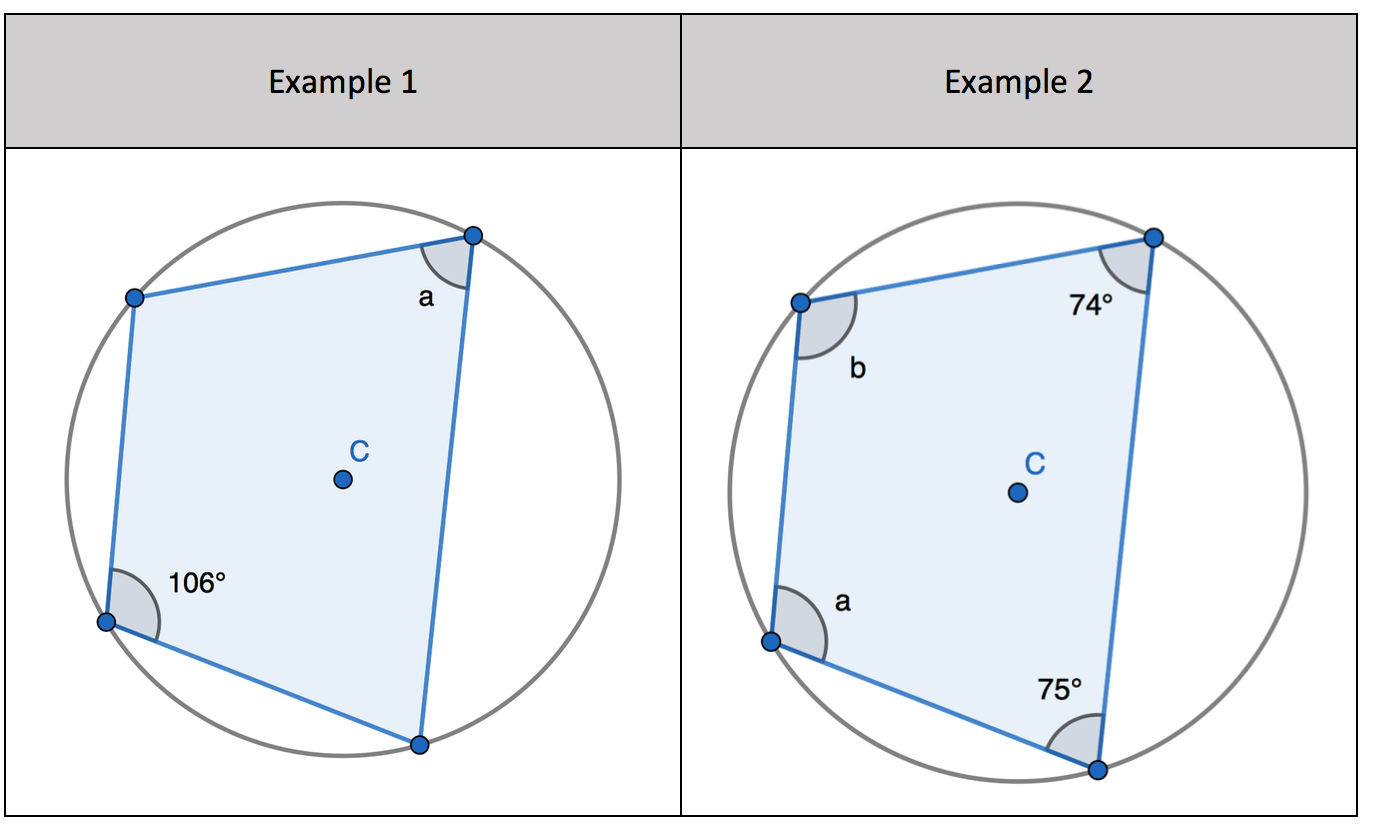 1. Find the opposite angle in the quadrilateral by subtracting the angle you have from 180 degrees
1. Find the opposite angle in the quadrilateral by subtracting the angle you have from 180 degrees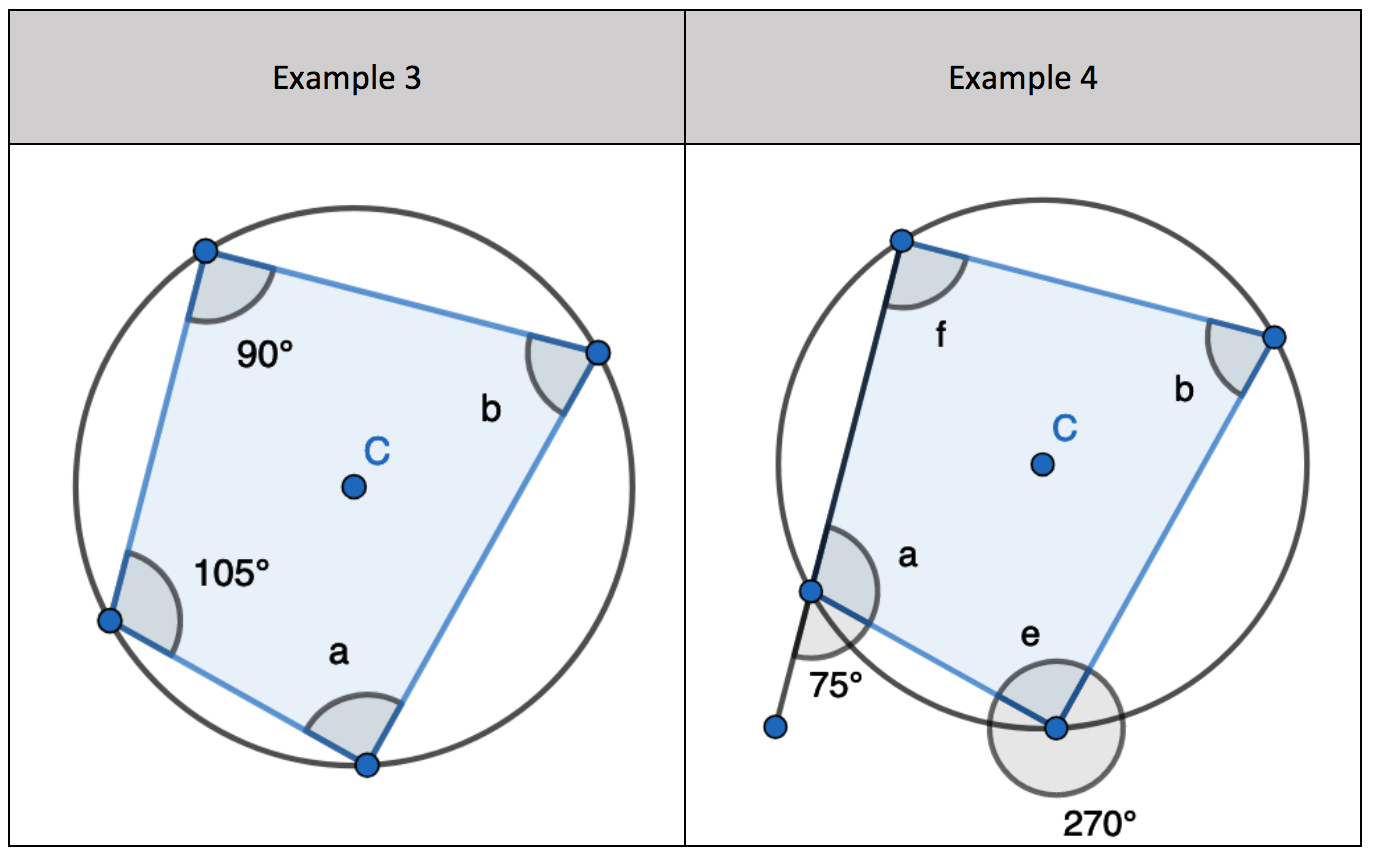
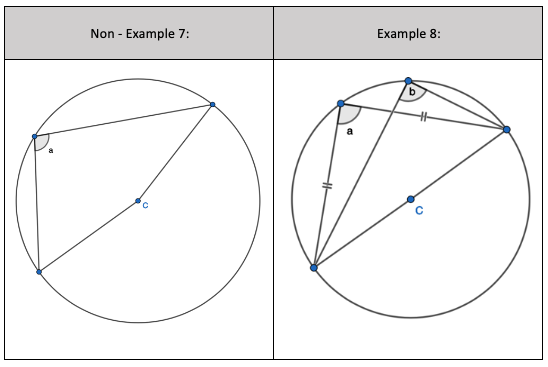
 5. Interleaving the first circle theorem – A right angle triangle in a semi-circle
5. Interleaving the first circle theorem – A right angle triangle in a semi-circle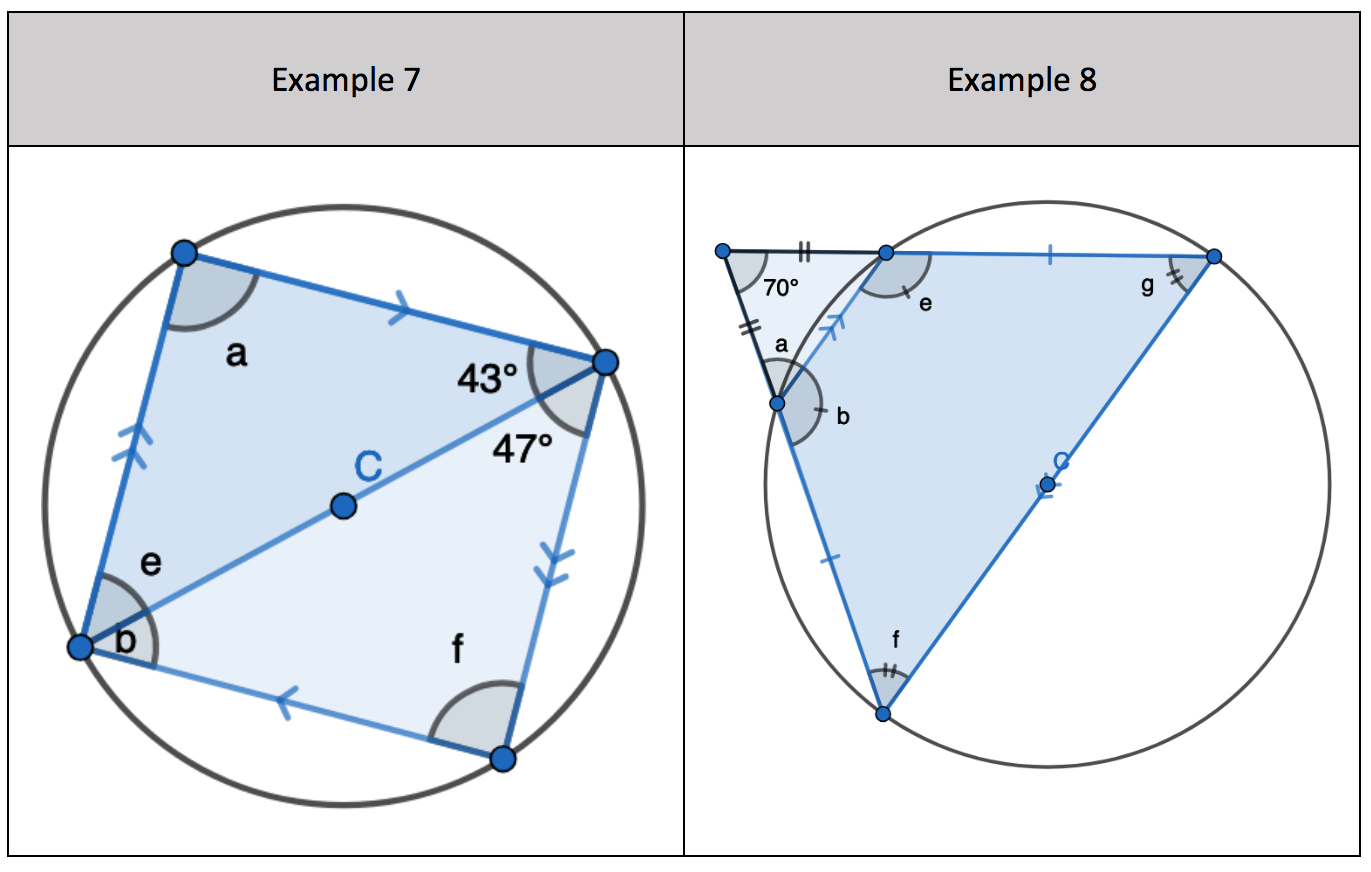 7. Interleaving the first circle theorem – A right angle triangle in a semi-circle
7. Interleaving the first circle theorem – A right angle triangle in a semi-circle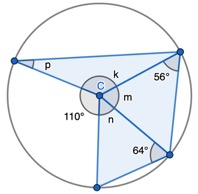
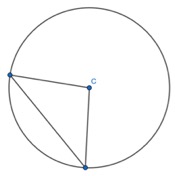
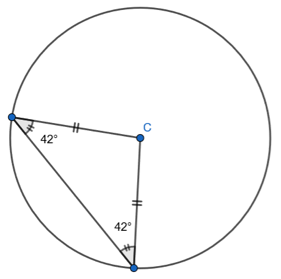
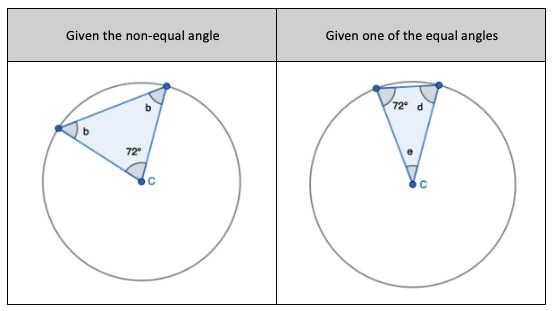
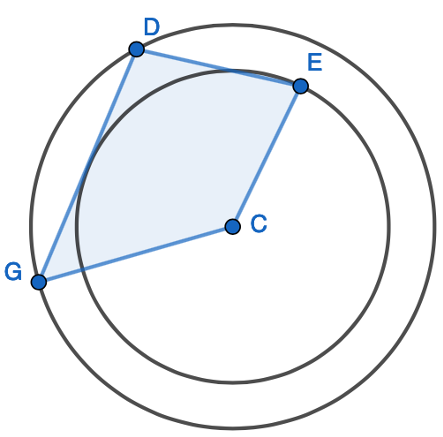
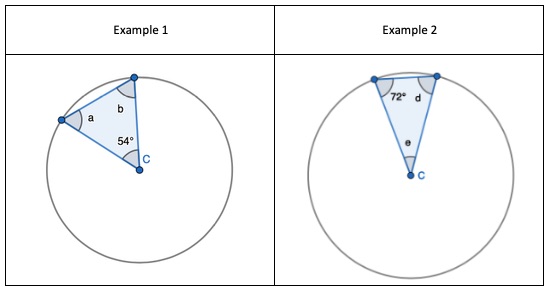 1. Show that two radii and a chord form an Isosceles triangle, only. Given the non-equal angle, find the one of the two equal sized angles.
1. Show that two radii and a chord form an Isosceles triangle, only. Given the non-equal angle, find the one of the two equal sized angles.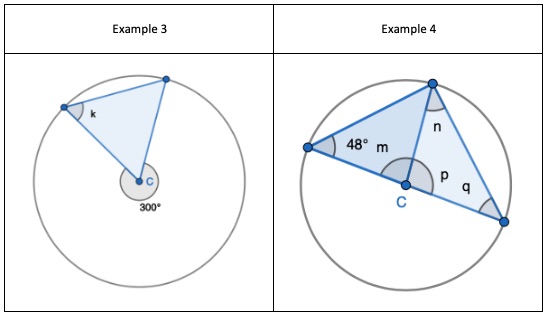








Recent Comments