Engelmann’s Connecting Maths Concept Textbook series teaches concepts that all future mathematical study relies upon. For example: the four operations, the relationship between addition and subtraction as well as the relationship between multiplication and division, fractions to simply name a few. In this blog post I will be looking at how the topic of fractions is taught within the first 100 lessons of Engelmann’s CMC textbook series (Level D). I will go through a number of knowledge facts or skills that Engelmann outlines.
Connecting Maths Concept Textbook Series
The CMC textbook series have multiple levels to select from to best suit the children who will be learning from the CMC textbook. I taught the Level D series. The textbooks served the purpose of acting as a remedial programme where pupils received 3-5 one-hour lessons per week on top of their mainstream maths lessons. There is a scripted teacher presentation book, a pupil workbook, pupil textbook and an answer key.
One note to mention on the scripted teacher presentation book. Many teachers do not like being given a teacher script because it seems unusual to teach using somebody else’s words. I felt this way initially. I then completely changed my mindset on this because the script was incredibly accurate, deliberate and economical with text. I realised that Engelmann has written it better than anything else I had seen. I found it to be a really humbling process because it made me realise that I had been very verbose with my teacher talk. I could say much more with fewer words. This is still a controversial topic in the Education world. However, I found that the script helped the children to articulate their understanding because they were able to repeat a precise explanation back to me, that was simply provided through the teacher script. This was something that @MrBlachford commented on too, on Twitter:
A few overarching points
The key theme that Engelmann demonstrates throughout his textbook series is using:
teaching methods of future learning which never contradicts the teaching methods used for prior learning.
There is total consistency throughout the teaching methods used and applied when learning a specific concept. This will be shown by outlining the teaching of 20 skills on the topic of fractions over a 100 lesson period. There is also a smooth track of gradual complexity in the problem types that are used to test a pupil’s understanding. The content that is taught looks deceivingly easy but pupils are taught teaching methods that can be applied in the most simplest of cases as well as the most complex of cases.
Engelmann’s lesson spread looks like this. The red sections are the teacher-led parts and the green sections are the parts where pupils work independently. Each lesson covers a range of 5-6 different topics such as adding, subtracting, fractions, times tables, ratio etc.
Breakdown of each teaching point
- Stating a fraction from a diagram
Engelmann introduces how to write a fraction from a diagram by using images where there was more than one unit, as shown below: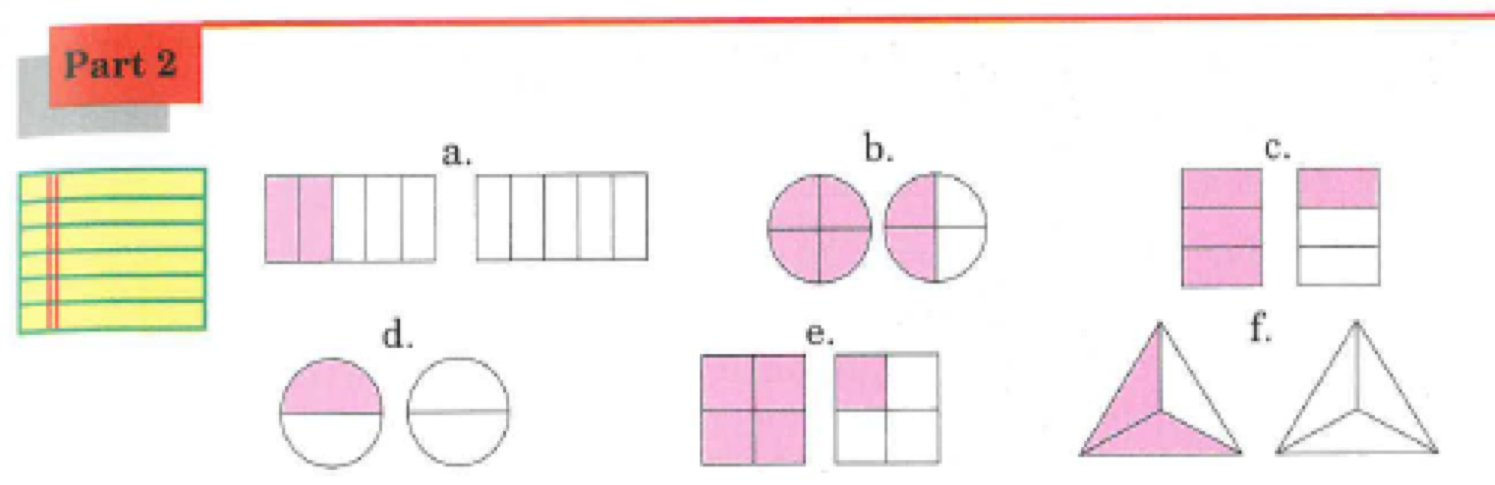
The wording to write a fraction was:
The top number is the total number of shaded pieces.
The bottom number is the total number of pieces in one unit.
The wording was precise, and fool-proof. I did alter the working to ‘the bottom number is the total number of pieces in each unit’ simply because my pupils responded to that with more accuracy. The wording applied to cases where pupils were writing proper fractions, improper fractions as well as whole numbers. The questions that were selected which tested this also:
The wording also avoided the common misconception that pupils have in writing the denominator as the total number of pieces that they can see between the number of shapes shown. This is because the wording say ‘in one unit’.
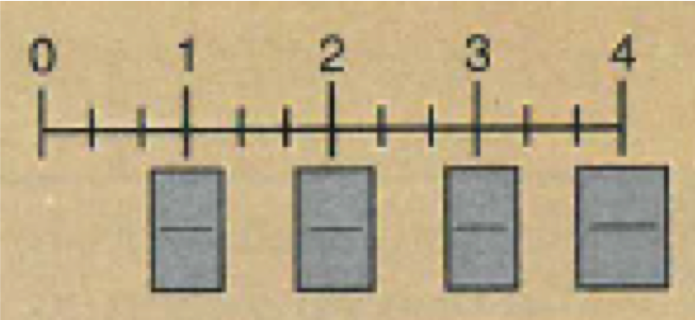
2. Stating a fraction from a number line
The same wording was introduced. I did explain to pupils that one unit was the gap between each whole number.
There were exercises where pupils were practising both skill #1 and #2 side by side.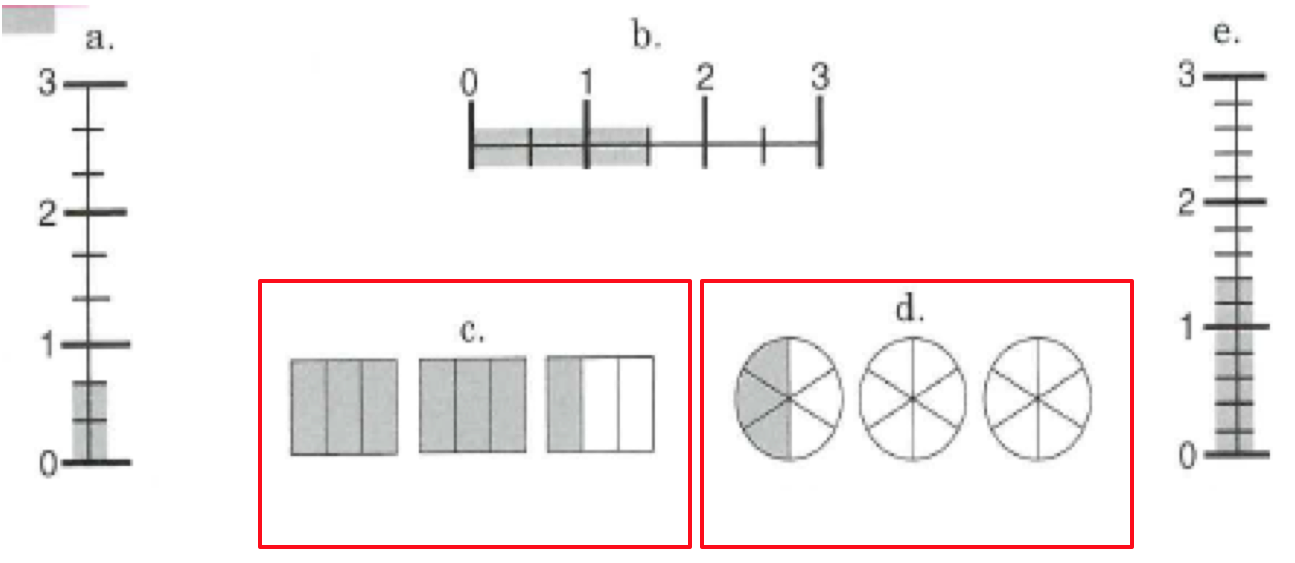
3. Stating whole numbers from a diagram or a number line
If you see a diagram or a number line where a certain number of units are shaded then the diagram or number line represents a whole number. The point is also mentioned that if there are no leftover parts are shaded then we definitely have a whole number. The opposite case is presented that if we do have leftover parts that are shaded then we don’t have a whole number.
The scripted nature of it states: “3 units are shaded. So the fraction for this picture equals 3.”
Similarly, there is a negative example of this where the script words what the teacher says as: “There are more than 3 units shaded, but less than four.”
The testing stage phrased the question as: which picture shows a whole number?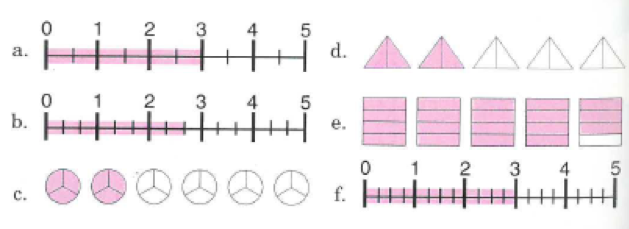
4. Fractions as integers from a diagram
For it to be the case that we are showing an integer visually then there is only one part in each unit, meaning that each unit is one whole shape. The number of shaded units is the top number. The number of parts in each unit is the bottom number. This method is consistent with previous problem types of stating a fraction from a diagram or number line. What I like the most about the sequence of questions is that the nuanced example is taught after the explicit examples. #4 is the nuanced example of stating a fraction from a diagram because its not as straightforward. Engelmann’s presentation book still uses the same wording to state a fraction from a diagram, which shows pupil that they are equipped to answer even the trickest of questions.
The wording to teach pupils how to state a fraction as an integer from a diagram goes as follows:
There is one part in each unit. 4 parts are shaded. The fraction for the picture is 4 over 1. Here is the equation: 4/1 = 4.
There is one part in each unit. 6 parts are shaded. The fraction of the picture is 6 over 1. Here is the equation: 6/1 = 6
I remember one of the boys in my intervention class, looking at the question and attempting it before I started going through it. He did say the correct answer, and he was really impressed with himself. I then asked him how he did it. His response was ‘using the way that you taught me’. He was able to apply the method taught for previous problem types in this case too with no teacher guidance.
Pupils were then asked to state a fraction as an integer from a number line as well.
Pupils completed testing exercises where they had to state a fraction which could simplify to an integer where each unit had more than one part. These exercises also tested a pupil’s prior learning alongside new learning content.
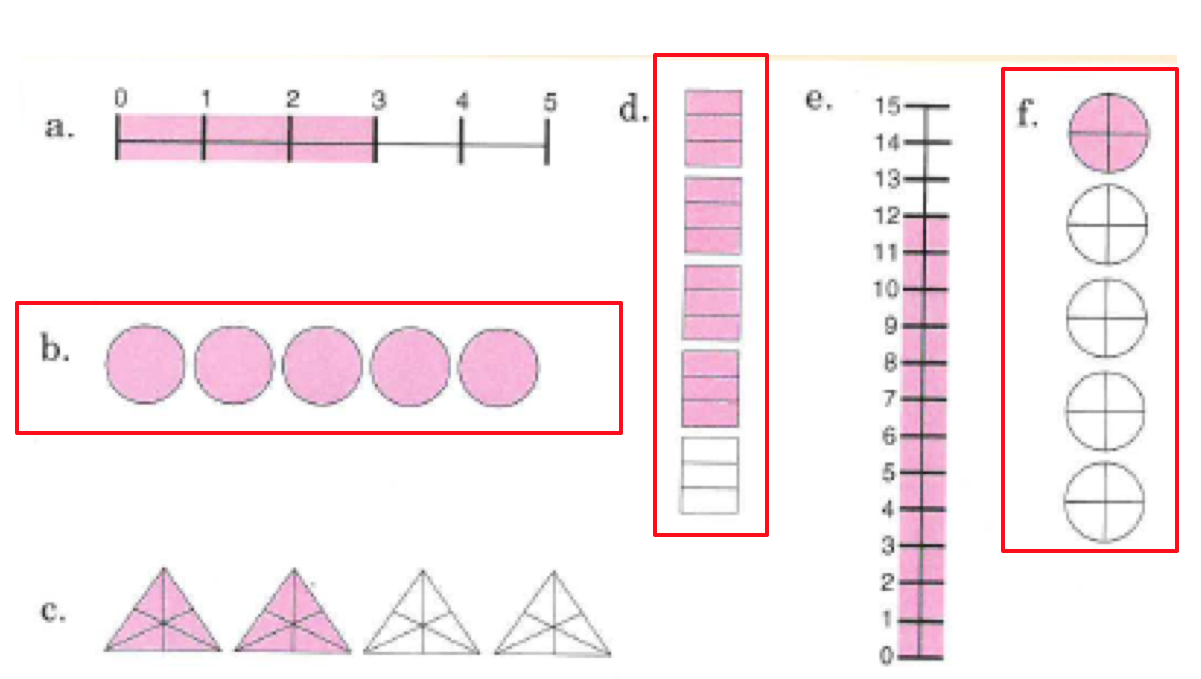 The most difficult problem testing skill #4 was asking pupils to write the fraction for each image that shows a whole number. Pupils are now applying collection of separate component skills where pupils are to: read a number line, write a fraction from the number line, and state whether that fraction is a whole number.
The most difficult problem testing skill #4 was asking pupils to write the fraction for each image that shows a whole number. Pupils are now applying collection of separate component skills where pupils are to: read a number line, write a fraction from the number line, and state whether that fraction is a whole number. 
The next degree of complexity introduced where now pupils need to state the fraction for each whole number on a number line.
Here is the wording used in the textbook:
There are three parts in each unit. So the bottom number of each fraction is 3. The bottom number for each fraction is the same:
The top numbers are the numbers for counting: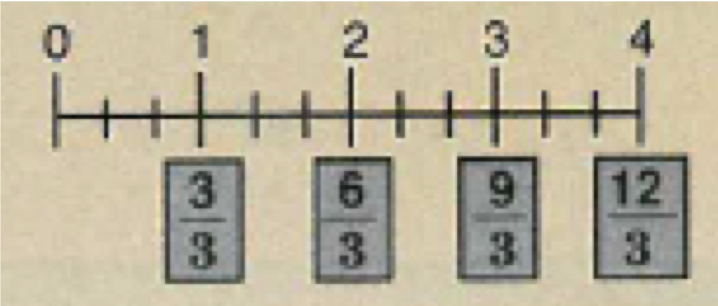
There are exercises further on in the series of lesson where pupils are given the same task but the number line doesn’t state the number of parts in each unit, instead the denominator is provided.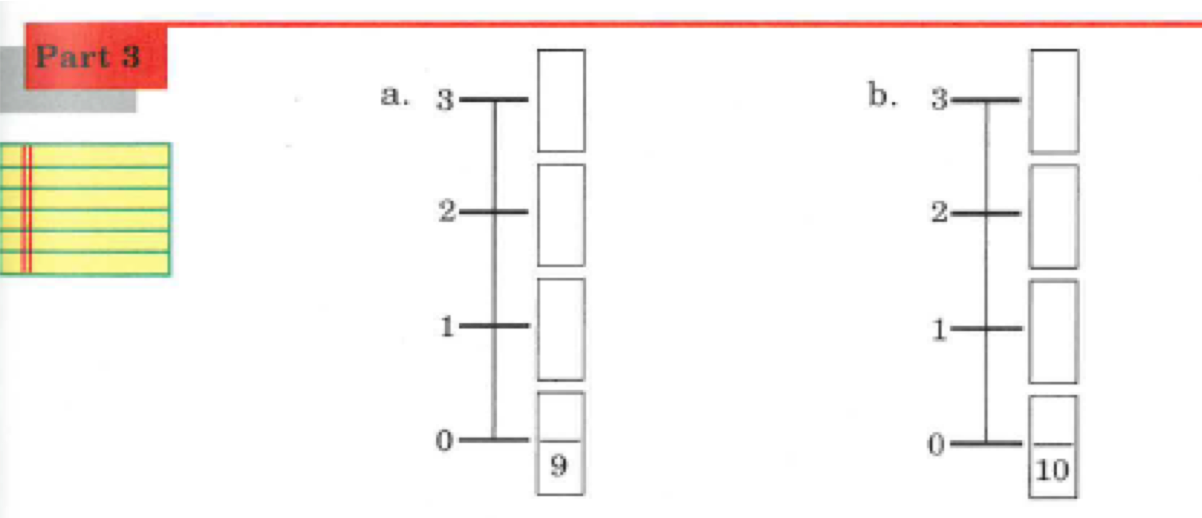
In my next blog post, I will continue to outline the remaining fraction skills that are taught in Engelmann’s sequence of lessons.




Leave a Reply
You must be logged in to post a comment.