This blog post is the fourth of a series ‘Reattempting Circle Theorems’. We have looked at the following circle theorems and a non-circle theorem:
Circle Theorem #1: A right angle triangle in a semi-circle
Show that: Two radii and a chord form an Isosceles Triangle
Circle Theorem #3: A cyclic quadrilateral’s opposite angles add to 180 degrees
We will now look at the next circle theorem:
Circle Theorem #4: Angles at the circumference in the same segment are equal
The booklet attached below follows the same structure:
- Starting with the circle and outlining its features to deduce the circle theorem
- Start with examples to find the missing angle(s) of
- the circle theorem in isolation
- interleaved basic angle facts
- interleaved previously taught circle theorems
- Algebraic section (In this case, I haven’t attached it because I would do it differently now)
Can you imagine your weakest children being able to find all the missing angles?
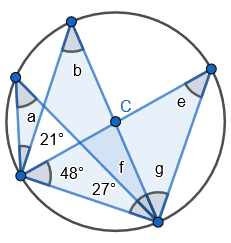
Introducing the Circle Theorem: Angles in the same segment are equal
Here is a circle:
Mark the first point on the circumference:
Mark a second point on the circumference:
Mark a third point on the circumference:
Draw a chord from the first point to the third point:
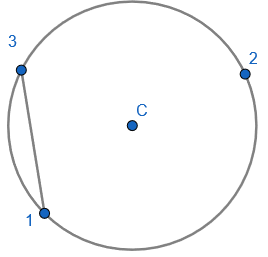
Draw a chord from the second point to the third point, and this forms the first angle:
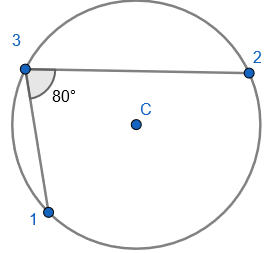
We can draw a chord between the first and second point, so we form two different segments. The angle is in the bigger segment. We can call this the major segment.
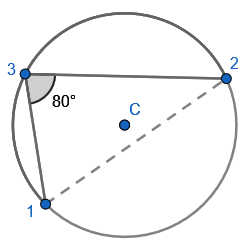
Draw a fourth point in the same segment, and draw a chord from the first point to the fourth point:

Draw a chord between the second and fourth point on the circumference, and this forms the second angle in the same segment:
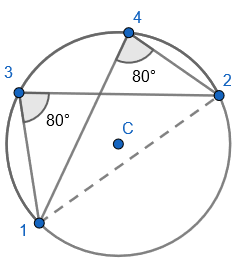
We can see that the angles are equal. We can see that using the first and second point on the circumference we have created two equal angles in the same segment.
Mark a fifth point on the circumference and draw a chord between the first and fifth point:
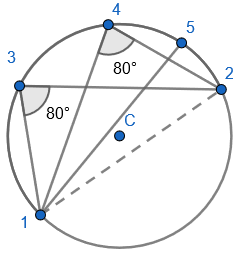
Draw a chord between the fifth and second point, to form an angle at the circumference in the same segment:
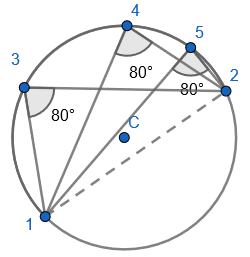
We can see that three equal angles made by the first and second point are in the same segment.
What if we mark a sixth point on the circumference that is the other segment?
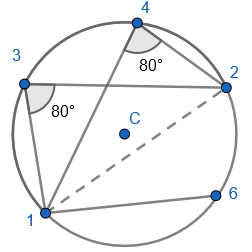
And we draw a chord between the second and sixth point to form an angle in the other segment:

We can see that the angle in the other segment is not the same size even though it is made by the first and second point on the circumference. It is not the same size because the angle is not in the same segment.
Pedagogical Quandary
As a side note, I’ve come to realise that there are a few different ways that teachers describe what’s happening here.
The first, which I was using, was to explain that any angles in the same segment, subtended by the same arc, are equal.
The second, is that any angles in the same segment, subtended by the same chord, are equal.
So, which is correct; which should we use?
Well, a chord necessarily forms an arc… and each unique chord forms a unique corresponding arc… so, if we know the chord, we know the arc, and if we know the arc, we know the chord. In other words, its redundant to use both, and we can choose either and be completely correct in what we’re saying.
For me, I used to use the language of ‘arc,’ but have chosen to now switch to the talking about the angles as subtended by the chord instead, since it’s the chord that splits the circle into different segments, not the arc.
You can’t avoid drawing in a chord at some point, to create the two segments, so discussing the arc as well, right up front, is probably just adding more unnecessary, extraneous cognitive load.
Even for me as a teacher, I was struggling to understand the point about the angles being in the same segment, since I wasn’t drawing in any chords… I felt like I was just saying the words, just getting kids to parrot back ‘angles in the same segment are equal,’ when even I couldn’t see where the segment was! I’m questioning the value using this whole ‘arc’ language now. This is something I saw yesterday at Mathsconf which confirmed that I felt needed addressing.
Find the missing angle using the Circle Theorem
At this point, I would state the steps to find the missing angle before looking at a few examples. Pupils can follow the steps if they lose track during the example explanation.
Here are the steps:
- Circle known angle
- Highlight the two lengths that form that angle
- Circle the two points at the end of each length of that circled angle
- Draw a dashed chord between the two points to show the segment that the angle is made
- Highlight the pair of lengths that form another angle in the same segment
- The angles at the circumference made in the same segment are equal
Here are the pupil-attempt (We do) examples to find a missing angle or angles. The variation between the examples isn’t evident here. I try to change one change at a time between the ‘I do’, and the ‘We do’ example. I’ll explain the thinking behind choosing each example:

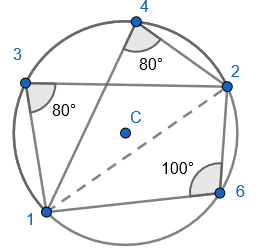
- State that angle ‘a’ is 60 degrees because the angles at the circumference are equal in the same segment.
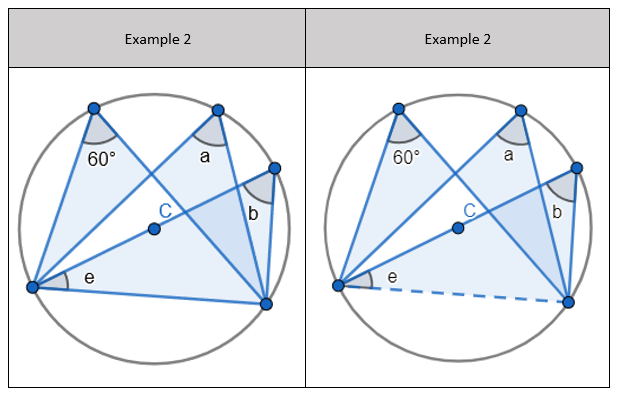 2. State that angle ‘a’ and ‘b” is 60 degrees because the angles at the circumference are equal in the same segment. Here we are showing that more than two angles are equal in size at the circumference from being in the same segment. I have interleaved the first circle theorem – an angle in a semi-circle is 90 degrees. If we total ‘b’ and 90 degrees to then subtract from 180 degrees then we can find ‘e’.
2. State that angle ‘a’ and ‘b” is 60 degrees because the angles at the circumference are equal in the same segment. Here we are showing that more than two angles are equal in size at the circumference from being in the same segment. I have interleaved the first circle theorem – an angle in a semi-circle is 90 degrees. If we total ‘b’ and 90 degrees to then subtract from 180 degrees then we can find ‘e’.
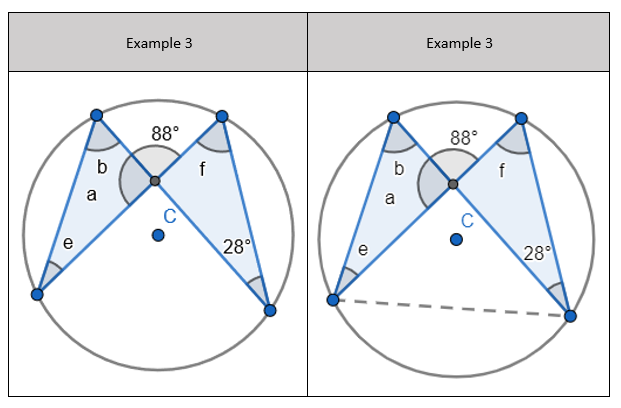 3. State that angle ‘e’ is 28 degrees because the angles at the circumference in the same segment are equal. Find ‘a’ using the basic angle fact that angles on a straight-line sum to 180 degrees. Find ‘b’ using the basic angle fact that angles in a triangle sum to 180 degrees. State that ‘f’ is the same angle size as ‘b’ because of the circle theorem we have just learnt.
3. State that angle ‘e’ is 28 degrees because the angles at the circumference in the same segment are equal. Find ‘a’ using the basic angle fact that angles on a straight-line sum to 180 degrees. Find ‘b’ using the basic angle fact that angles in a triangle sum to 180 degrees. State that ‘f’ is the same angle size as ‘b’ because of the circle theorem we have just learnt.
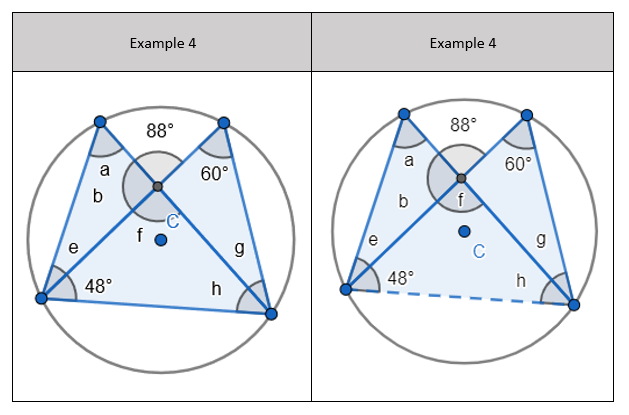
4. This is the same problem type as the third example but now I’ve added a chord to form a triangle with angle ‘f’, ‘h’ and ’48 degrees’. We can find ‘f’ to be 88 degrees because it is vertically opposite to it. We can find ‘h’ using the basic angle fact that angles in a triangle sum to 180 degrees.
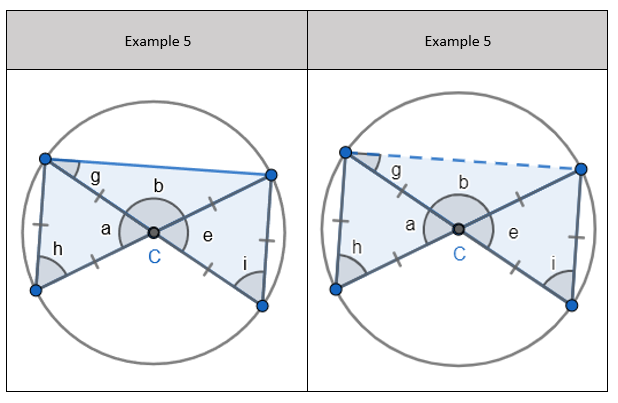 5. Pupils can see that there are two equilateral triangles meaning ‘a’, ‘h’, ‘e’ and ‘I’ are all 60 degrees. I would mention that angle ‘h’ and ‘I’ are equal because those angles at the circumference are in the same segment.
5. Pupils can see that there are two equilateral triangles meaning ‘a’, ‘h’, ‘e’ and ‘I’ are all 60 degrees. I would mention that angle ‘h’ and ‘I’ are equal because those angles at the circumference are in the same segment.
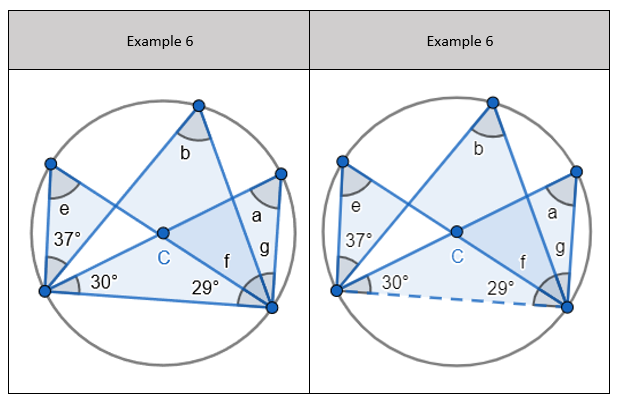
- State ‘f’ is 37 degrees because angles at the circumference made in the same segment are equal. Find ‘g’ because the total of ‘f, ‘g’ and 29 degrees is 90 degrees because the triangle is right angle triangle. We know this because the hypotenuse of the triangle is also the diameter of the circle. Find ‘a’ using the basic angle fact of angles in a triangle sum to 180 degrees. State that ‘a’, ‘b’ and ‘e’ are all angles at the circumference made in the same segment. They are equal to 60 degrees.
Booklet attached below:
https://drive.google.com/open?id=1gaJvcsgimiHEyPVho-U3NWyZ2hWmuj95
Leave a Reply
You must be logged in to post a comment.