When are teachers to generalise a procedural calculation to apply to all problem types? When are teachers to display all the different problem types for a particular generalised procedure? I always jump between generalising and displaying different problem types, including not stating that one technique is better than the other but stating that in some instances one technique can be prioritised over the other.
In Maths there are many generalised procedural calculations which are true for all problem types of a concept. For example, listing a step by step process for pupils to follow which exists for all problem types regardless as to whether the problems include integers, decimals, percentages, numbers in index notation and square roots etc. in the problem type. We can try to create all the possible visual forms of a problem type, where generalising a procedure is a great teaching technique because it allows pupils to demonstrate efficiently their understanding by outlining the algorithm between the problem and the solution – step by step.
Here is an example of generalising the step by step method in order to add fractions with unlike denominators:
- Find the lowest common denominator.
- Form the equivalent fractions.
- Add/subtract the numerators.
This generalised algorithm is also applicable in instances of adding or subtracting like fractions; but pupils already have the lowest common denominator, and the fractions being added or subtracted are in their equivalent form, and so only step 3 is applicable. However, adding like and unlike fractions are seen as two distinct procedures, when a question with like fractions is a similar problem type to where step 1 and 2 are already completed.
A generalised procedure to adding and subtracting fractions is applicable for the following problem types where we have improper fractions, mixed numbers and a mixture of the two, or with calculations using more than three terms. Even through each example looks visually different, distinct and more or less challenging than the other, the generalised procedure is applicable.
Generalised procedures are great for pupils to develop their procedural understanding. Further, by discussing, in addition, the different problem types of adding fractions it can empower pupils further. The reason why I say this is because this generalised form of adding fractions neglects the different problem types that exist for this topic and many others. Here are the three different problem types I am referring to:
- Fractions where the dominator are alike (LCD already present)
- Fractions where the denominator are co-prime (share a factor of 1)
- Where the LCD is the product of the denominators
- Fractions where the denominator are not co-prime (share a factor greater than 1).
- Where the LCD is provided as one of the denominators
- Where the LCD is not the product of the denominators.
Exploring different problem types leads to a greater development of knowledge and understanding which can be applicable in instances such as the problem types below:
‘A’ builds on the knowledge of the problem type where the denominators are not co-prime and where the LCD is provided as one of the denominators.
‘B’ builds on the knowledge that the denominators are co-prime and therefore the LCD is a product of all three denominators.
‘C’ builds on the knowledge where the denominators are not co-prime but the LCD is not the product of the denominators.
Can the teaching of problem types alongside the generalised procedure be beneficial in the other realms of mathematics such as algebra, geometry or data? Possibly, here is an example of expanding double brackets in a generalised form as well as exploring the different problem types.
The generalised form can be summarised into the following steps:
- Draw a 2 by 2 grid.
- Write each term of the expression in each section of the grid.
- Multiply all the different terms.
- Collect and simplify.
Furthermore, this generalised form allows even the most visually complex problem types to be solvable for pupils, as per the below:
- (2x + 3)(3 + 2x)
- (ab + cd)(2ab – fg)
The intention of generalising is not to make model algorithms for pupils to replicate. The point is to empower pupils to be able to look at the features of a problem, identify the problem and identify the route between the problem and the solution for every possible problem, regardless of how complex or simple the problem is.
The generalised procedure is applicable in all four different examples of multiplying two binomials to form a quadratic expression, where the expressions multiplied are in the following forms (a and b represent different values):
- (x + a) (x + b)
- (x – b) (x – a)
- (x – a) (x + b)
- (x – a) (x + a)
Discussions can then take place where pupils can begin spotting patterns, that:
- the product of two binomials where the constants are positive, the second term will have a coefficient which is the sum of the constants. (x + 2)(x + 1) = x2 + 3x + 2.
- the product of two binomials where the constants are both negative will have a constant which will be positive because the product of two negative numbers results in a positive number (x – 2)(x – 3) = x2 – 5x + 6.
- the product of two binomials where one constant is negative and the other is positive then the ‘c’ term will be negative.
- a difference of two squares will result in no ‘b’ term because the terms will result in 0 and the ‘c’ term will always be the square number of the constant in the binomial (x – 2)(x + 2) = x2 – 4.
To conclude, generalising a procedural calculation for all problem types, and exploring different categories of problem types for a concept, can be incredibly valuable because pupils start spotting patterns which can increase their confidence when learning. Primarily, enables pupils to be able to identify the problem and the correct generalised procedural calculation required to find the solution. Now, I believe that pupils will learn when to apply the generalised procedural calculation to a problem type if they are shown the different problem types that can exist. Yes, for some topics there are hundreds of problem types that can be explored, but then generalising the procedural calculation is even more important; for a select few topics the practice questions can be categorised into different problem types.
I am still getting my head around it all, but would love to hear people’s thoughts.

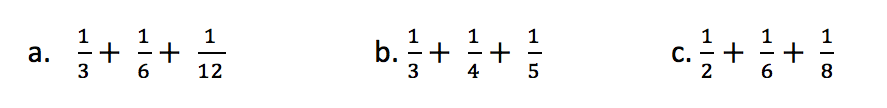
Leave a Reply
You must be logged in to post a comment.