Chapter 21, in Engelmann’s Magnus Opus, Theory of Instruction has changed the way I sequence worked examples to communicate a concept. This change took place greatly whilst I was at Michaela Community School when I started experimenting how to teach a UK Maths Challenge After school club. This is written about in more detail, here.
What I noticed, which may sound obvious, is that if you teach using examples which demonstrate the explicit features of a concept first and then progressively make those features implicit then the probability of success for each child in the learning process is greater. Engelmann refers to this as Covertization, “instruction that involves prompt shifts progressively from highly-prompted examples to unprompted examples.”
One example which will be detailed below, would look like this:

So a sequence of examples with explicit features transitioning to implicit features provides a process where pupils take overt steps to go from the first line of working to the last line of working. This means that the first example pupils encounter is structured within the simplest context.
Covertization results in examples that communicate a concept, or part of a concept, to be communicated in its most explicit and misconception-proof form.
The best way to appreciate covertization is to look at some examples which aren’t explicit.
Here are examples of fractions:
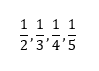
Here pupils can develop the following misconceptions:
- all fractions have a one at the top
- all fractions increase by ‘1’ in the bottom value
- fractions get bigger when the bottom value is greater
Another example:
Here are examples of expressions commonly known as a ‘difference of two squares’
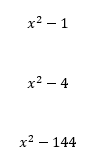
Here pupils can develop the following misconceptions:
- The first term is always positive and a
- The second term is always a constant
- The second term is always an integer
- The second term is always negative
What are the examples that I would use instead? To communicate an expression as a ‘difference of two squares’ I would start with the following, by stating that an expression must meet the following conditions:
- The coefficient of the variable is a square number
- The power of the variable must be even
- The power of the variable is never an odd number
- One term will be negative AND the other term will be positive
- The constant must be a value that can be square rooted.
Here are the following examples that I would use to reiterate the conditions stated above:


There are other examples that I could include here, however, what I’ve done is limit the examples to only meet the conditions I’ve stated. But look at the complexity of what pupils can identify as an expression known as a difference of two squares by selecting the examples that I have.
More importantly, I’ve started with an example which is explicit with the features that make an expression a difference of two squares. With the initial set of examples, you can see that the coefficient of 1 for isn’t obvious because pupils can’t see it, and ‘1’ as a constant isn’t an obvious example of a square number. Explicit features allow pupils to build a clear and misconception proof understanding of a concept, which is what makes an example powerful.
My final point, we can see that the process of covertization has highly prompted examples allowing pupils to respond successfully to writing the product of two expressions because the coefficients and powers provide them that structure. Starting the other way around with implicit features now looks unstructured and poorly guided for a pupil to know how to rewrite the expression as a product of two expressions.
Leave a Reply
You must be logged in to post a comment.