A month ago, I was resourcing for the topic ‘Expressions and Substitution’ for the Y9 Curriculum. A common approach is to substitute values to then solve a linear equation. I was keen to create a problem type when you substitute values you then have to solve a quadratic equation. Something like this:

On the surface you can see that the sequence of examples have one aspect varied at a time – value for ‘u’. This is inspired from Ference Marton’s Variation Theory (VT). One theory out of a body of educational research underpinning the United Learning Mathematics resources.
We use VT because perceived variation generates expectations for pupils. When these expectations are confirmed pupils’ perceptions are relevant mathematically. VT guarantees more clarity and honesty about mathematical ideas. Anne Watson and John Mason explain the meaning of ‘clarity of mathematical ideas’:
“the structure of examples through which learners encounter mathematically significant variation…attention can be focused on the use of variation to reveal the patterns and generalities which result from the techniques. This is the clarity.” ¹
This blog post will look at how VT is applied on the surface by changing the value of ‘u’, but also resulting in one change in the procedure of factorising a quadratic expression. This post is about the thinking behind creating an exercise like this, teaching it would be different post. To appreciate what follows here is the working out for part (a) and part (b)

On the surface, you can see that only initial velocity’s value changes. This is deliberate. Under the surface, here are the quadratic equations for each part to show that only one thing is changing between each part:
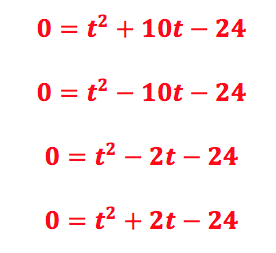
Pupils overgeneralise the procedure of substituting values to then solve a quadratic equation.
This example shows variation on the surface, but also with the quadratic equations solved so pupils develop mathematically relevant expectations that they will be solving a quadratic equation.
Here is the thinking process behind making this exercise:
Step 1:The kinematic equation where t is unknown results in solving a quadratic equation:
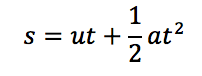
Step 2: I then thought what would have to be the unknown variable and the known variables? For the following formula to result in a quadratic equation t is unknown.
Step 3: In Y9, pupils can factorise a quadratic expression where all coefficients and constants are integers, and where the coefficient of ‘a’ in a quadratic equation of ax² + bx + c is equal to 1, only, not greater than or less than 1.
I have to be selective with each known variables’ values. Some are permissible and where some aren’t. The values that aren’t permissible would mean pupils factorising a quadratic expression where ‘a’ in ax² + bx + c is greater than 1.
Step 4: I looked at a sequence of quadratic expressions that can be factorised. Variable t will be the unknown rather than x to correspond to the kinematics equation:
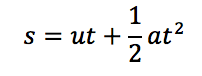
So, here is the sequence I made:
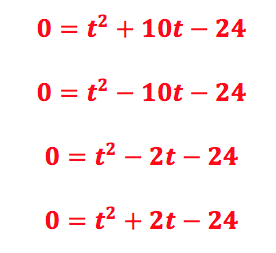
There are a few expressions that I can’t factorise because of the context of the kinematics. During the solving process, I can’t have two values of t being equal to a negative value. I can’t have this situation below:

In the context of kinematics, I can’t have negative values for time. Deciding which one to pick will confuse pupils.
I can have either: a quadratic expression where t would be both positive, or one value of would be positive and the other negative. If there are two positive values for time, then that means the case is true at two different times. If one value of time is positive and the other is negative, then we accept the positive value for time only. In sum:
I can’t have a quadratic expression where the constant is positive AND the value of ‘b’ in ax² + bx + c is also positive.
I can have a quadratic expression where the constant is negative AND the value of ‘b’ in ax² + bx + c is either positive or negative.
Step 5: Back to the condition stated in Step 3 where the coefficient of ‘a’ in a quadratic expression of ax² + bx + c is equal to 1, only.
For this to be the case, I know that
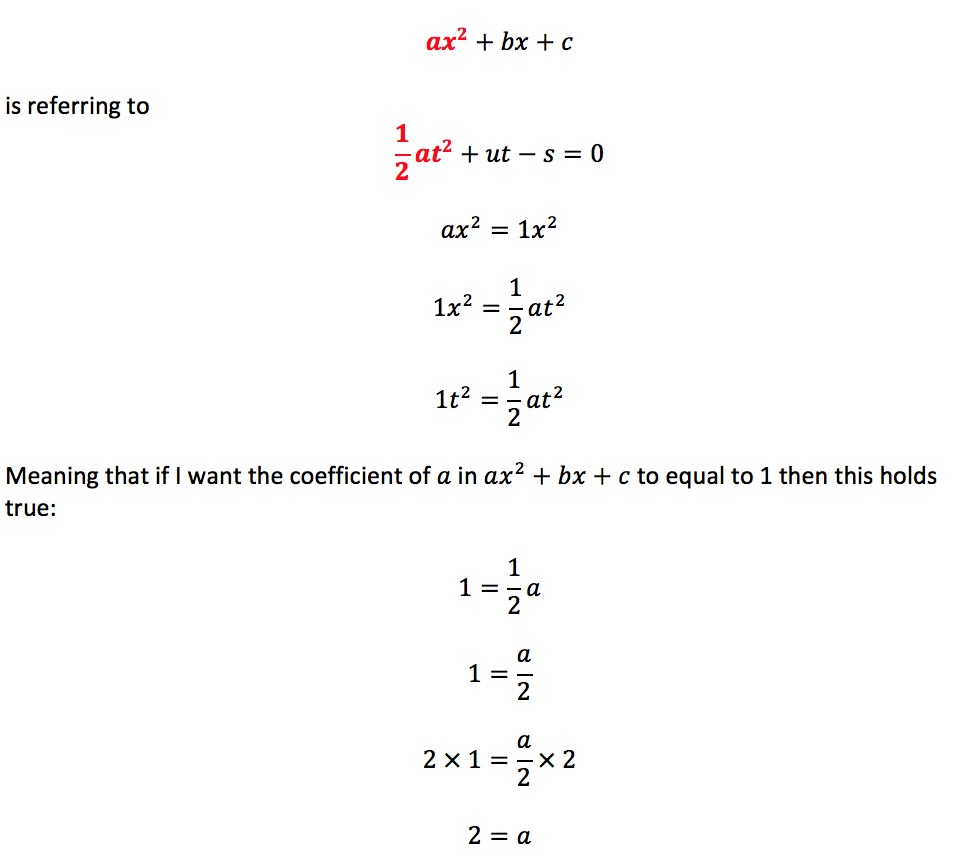
The value of ‘a’ cannot vary, because pupils will have to factorise a quadratic expression where ‘a’ in ax² + bx + c is greater than 1.
Step 6: If we look back at the sequence of quadratic expressions, I have kept the value of the constant the same -24. And since,
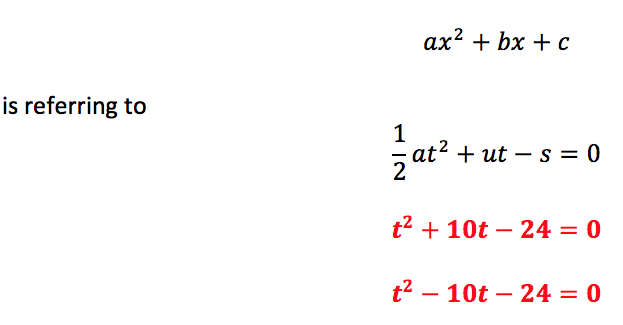
The value of ‘a’ and ‘s’ remain the same throughout so the only varying value is for ‘u’ . Initial velocity can be positive or negative because it is a vector quantity.
In summary, on the surface of the exercise only the value of initial velocity varies at a time. Beneath the surface, one coefficient of the quadratic expression varies at a time. We are varying on the surface and deep within the mathematical problem. The two controlled dimensions encourages the learner to find the value of t:
- By overgeneralising the process of substituting to then solve a quadratic equation.
Pupils focus on this overgeneralisation because they can factorise the quadratic expressions used. They learn the mathematical structure to substitute and solve a quadratic equation.
- References:
¹ Anne Waton and John Mason (2006) Variation and Mathematical Structure MT194
This exercise is under review. If you spot an error or have any feedback then please feel free to get in touch.
Leave a Reply
You must be logged in to post a comment.