In February 2018, I heard Andrew Blair speak at a CPD event about Inquiry Maths. Andrew is a Head of Maths and founder of his website Inquiry Maths where teachers can gain access to ideas about teaching Mathematics using the Inquiry Maths model.
Andrew and I tend to disagree over the best pedagogical approach when teaching Mathematics, but we agree in teaching many of the problems that he has shared on his website. When I create resources, I check out different sites for ideas, and I regularly check Andrew’s website. It’s fantastic! When I saw Andrew speak at this CPD event, he showed a mathematical inquiry task that I made a mental note to include in my resourcing for the following year. The problem is below:
40% of 70=____% of _____
I love this type of mathematical problem. There is so much mathematics that needs to be communicated, and I would recommend readers to check out Andrew’s page on this inquiry. At United Learning I’ve finished the Fraction, Decimals and Percentage booklet for the Y8 curriculum and I’ve made resources for this type of mathematical inquiry to be shared with the kids.
Here is an example of how I broke down the teaching sequence so all pupils can access a problem like this but also support all pupils to attempt more complex forms as well.
The teaching sequence is designed to increase the probability that all pupils can be successful in learning the subject content.
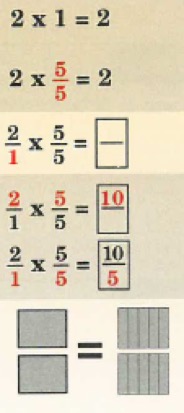
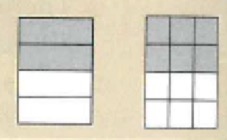
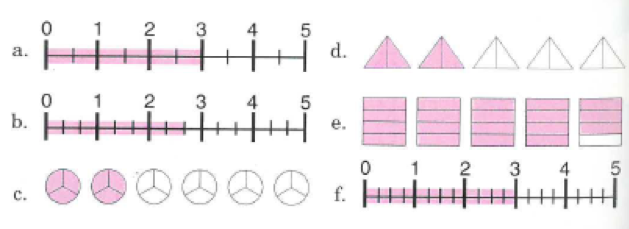
1) Showed a multiplication model for the following problem types
I have listed some of the potential decimal multiplication calculations and then demonstrated how to draw the model for the equivalent decimal multiplication calculation:
Pupils are only shown the first line because they are taught that the mathematical model of rewriting the decimal multiplication calculation.
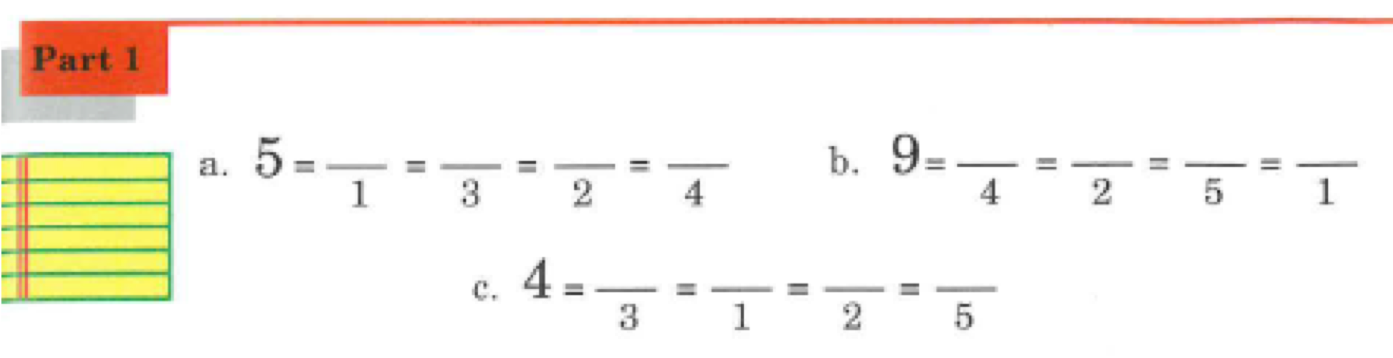
A few points: I’ve deliberately kept the position of the mixed number or decimal and the integer in the same place within the calculation. In the second example, the first term of the calculation is a mixed number and the second is an integer, it is the same on the right-hand side of the equal sign. This is because I want pupils to focus on the digits changing position, and that only. Everything else is kept constant.
This is how I would communicate the model in the classroom to pupils:
I am multiplying a two decimal places decimal by an integer, so my equivalent calculation will have a two decimal places decimal and an integer.
I would get kids to draw the underlines to show me how their equivalent calculation would look. I have done this because learning the mathematical structure of the calculation is another thing a pupil needs to learn. This also reduces the likelihood of a future error caused by pupils by not knowing whether the calculation will have an integer and a decimal, or an integer or a decimal, and how many decimal places the decimal will have.
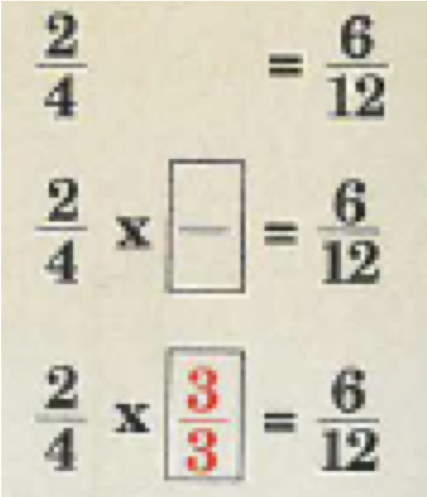
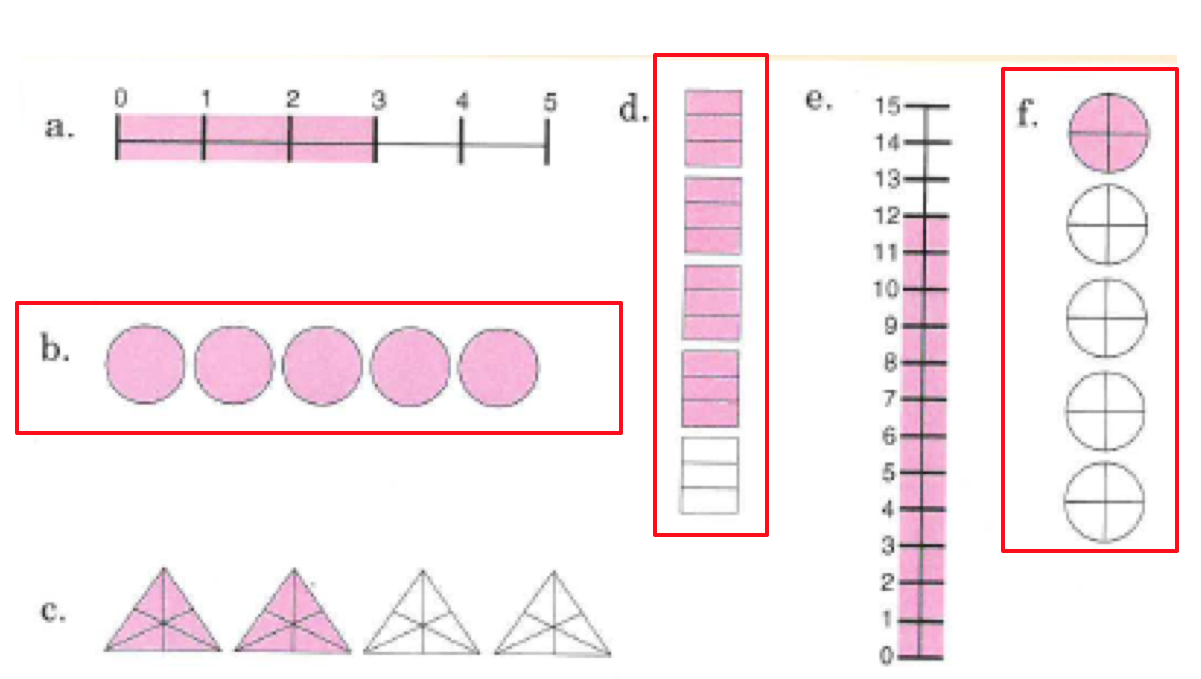
2) Introduce the steps to go from the problem to the equivalent calculation
a) Rewrite decimal place structure
b) Fill in the digits from the right side
c) CHECK: Multiply out both sides of the calculation to see that the result is the same
In my teaching, I write the generalised steps for the calculation pupils are about to do because they can see that even if I am rewriting a multiplication calculation with
- an integer and decimal or;
- two decimals or;
- decimals with the same number of decimal places or;
- decimals with a different number of decimal places
the generalised steps remain the same.
Generalising method stops is something that Siegfried Engelmann calls ‘Logically Faultless Communication’ which has been blogged about here.
A logistical thing, it also allows pupils to follow the steps better if they can flicker their eyes from the live worked example demonstrated by the teacher and the steps already written on the board.
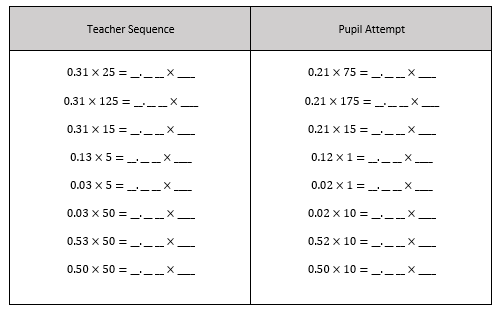
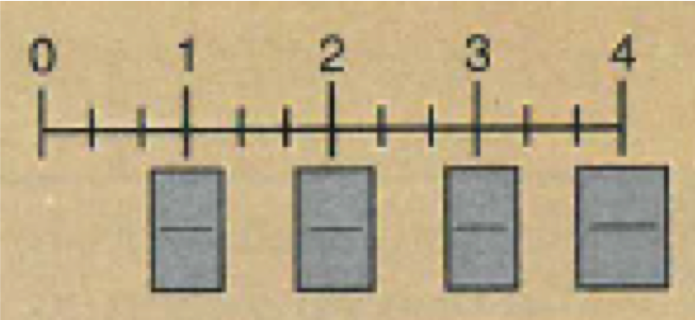
3) Introduce the Example-Pupil attempt sequence
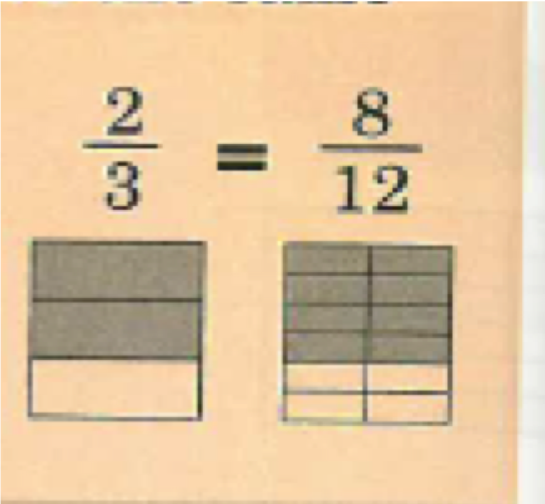
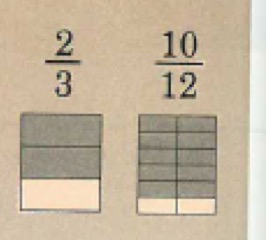
At this point, I then design the teacher-led worked examples and the pupil attempt questions. The problem type that the teacher goes through and the pupil goes through after seeing the teacher demonstrate the same problem type.
Here is the sequence:
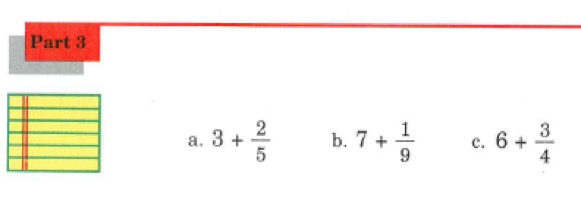
Pupils aren’t evaluating the calculation. They are rewriting the calculation so their answers would look like this:
I have deliberately started with explicit examples meaning that the 2 decimal places decimal and two-digit integer have digits more than 0. Only from example 4, I have introduced a single figure of 5; this is because pupils must write the digit 5 as 0.05 where there is a zero between the decimal point and the 5. Starting with explicit features such as digits more than 0 in decimals and integers makes the change from one calculation to the equivalent one more clear.
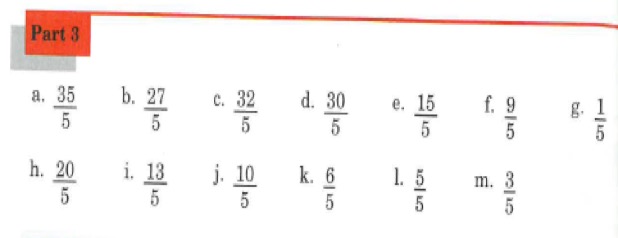
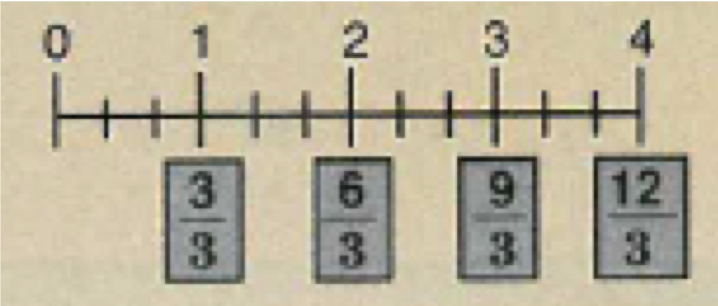
Pupils then will complete a practice exercise where they will rewrite a decimal calculation but ending in the same result as the first decimal calculation.
They will then transition onto a filling in the blank exercise like shown below:
4) Equating Percentages: Introduce the Example-Pupil attempt sequence
I believe that I’ve now taught all the prior knowledge pupils need to complete this statement:
40% of 70=____% of _____
The prior knowledge is listed below:
- Writing a percentage in its equivalent decimal form
- Rewriting a decimal multiplication calculation in a visually different form but where the result is the same as the original calculation
- Decimal place value
- Evaluating decimal multiplication calculations
Given that the prior knowledge has been taught and committed to long term memory, there is only one new thing pupils need to learn to complete the statement. They need to write the percentage as a decimal and replace the ‘of’ with a multiplication sign. Then every other line of working is prior knowledge that has already been covered.
Here is the working out, and the new line of working is in bold:
40% of 70 = ____% of _____
0.40 × 70 = __.__ __×____
0.40 × 70 = 0.70 × 4
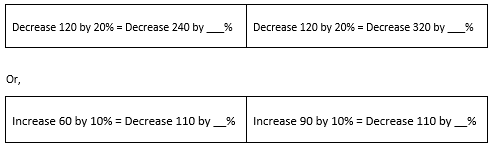
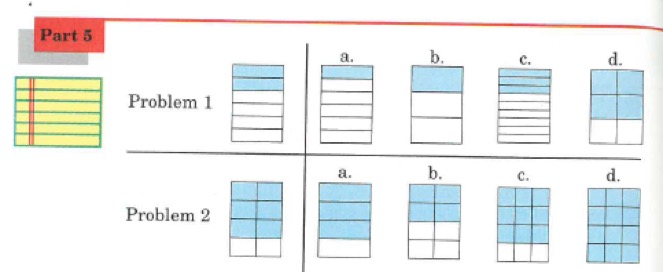
5) Comparing Percentage Increase/Decrease
What has been learnt here can also be used to complete statements like this below, and place the correct symbol between the statements <, > or =
6) Equating Percentage Increase/Decrease
The next level of difficulty that is accessible because of the prior knowledge taught is that pupils can evaluate the complete statement and equate the result to the incomplete statement.
Here the new knowledge being taught is dividing the result by the value in the incomplete percentage calculation.
However, what makes this more complex is that you must evaluate the complete calculation and equate the result to the incomplete calculation to then find the missing percentage. So pupils must:
1) Convert the decimal into a percentage
2) If the calculation is a percentage decrease, then subtract the percentage from 100%
3) If the calculation in a percentage increase, then subtract the percentage from 100%
Summary
I appreciate all the beautiful problems and mathematical tasks that Andrew provides on his website. They are incredibly rich in knowledge and can create a valuable mathematical conversation between teachers and pupils. There is a great deal of importance in teaching inquiry tasks because it is an opportunity to develop a flexible understanding of the subject. However, where I would disagree with the Inquiry Maths model would be how the mathematical task would be used and how the content would be taught to children. I think there is a great deal of prior knowledge that needs to be sequenced, so all future learning is supported by prior learning, and that only one new thing is being taught at each part of the sequence. This is to avoid cognitive overload.
I hesitate to have pupils taking responsibility for directing the lesson because each child will focus on a different aspect of the mathematical problem in front of them. More importantly, they will focus on various aspects depending on what knowledge they already have. It is inevitable that in any learning experience, each pupil will be starting at a different point based upon how much knowledge they have. However, when pupils direct the lesson that will result in more knowledgeable peers leading the lesson, and weaker pupils struggling to identify or learn aspects of mathematics that they need even to attempt the mathematical problem. By laying out the prior knowledge and sequencing it, you are allowing the more knowledgeable pupils to consolidate any existing knowledge they may already have, but you are letting the weaker pupils close any gaps they may have. Overlearning is an essential part of the learning process; it helps the more knowledgeable pupils to learn something to the point that they never make a mistake.
This attempt, I believe allows all pupils regardless of their knowledge gaps to have any missing gaps filled, but also allows all pupils to be able to access the mathematical problem.



















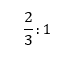
























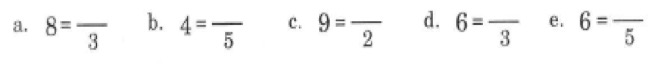




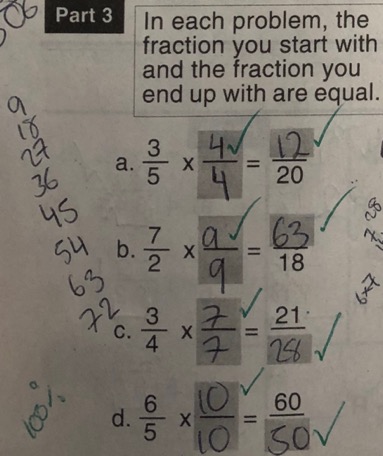


















Recent Comments