This blog post is the third out of four posts outlining the teaching and sequencing of various fractions skills taught in the Connecting Maths Concept Textbook series. Specifically, Level D. The first blog post can be found here. The second post can be found here. The following content was shown at La Salle’s National Mathematics Conference in Kettering.
10. Introducing Mixed numbers
Mixed numbers are introduced as a sum between an integer and a (proper) fraction.
 It is visually presented on a number line, you go to the marker for the whole number. Then you count parts for the fraction.
It is visually presented on a number line, you go to the marker for the whole number. Then you count parts for the fraction.
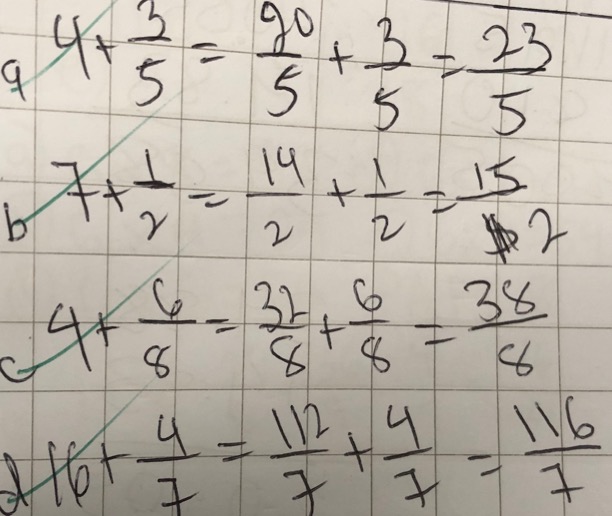
The skill is revisited where pupils write the addition sum between an integer and a fraction as a mixed number, without the number line. Pupils are then asked to do this again with three or four digit numbers.
Pupils also complete exercises where they:
- write an improper fraction as a sum between an integer and a proper fraction
- show the sum of an integer and fraction as a sum of two fractions
11. Multiplicative relationship between an integer and a fraction’s denominator
Pupils have been taught previously how to list a string of equivalent fractions equal to an integer, listed as skill 8. This was done through the use of their times table facts. Similarly, pupils are now taught how to find the missing numerator of an incomplete fraction equal to an integer.
12. Equivalent fractions from a diagram
Pupils are taught that:
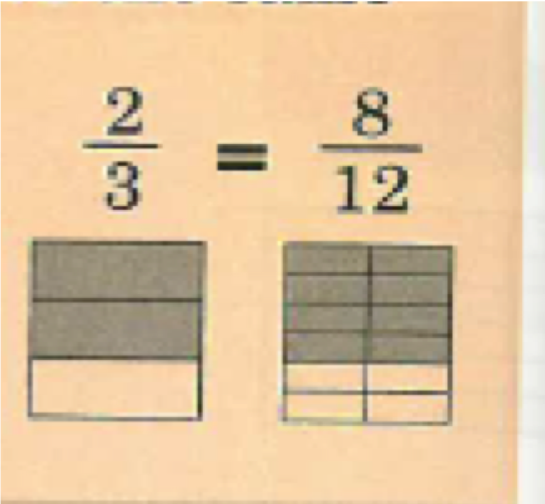
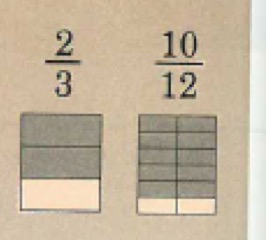
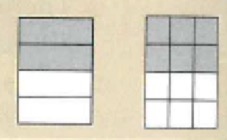
If fractions are equal, pictures of each fraction will have the same shaded area.
If the fractions are not equal, then the pictures do not have the same shaded area.
A teaching point to mention, I got the pupils to use a ruler to check to see if the shaded areas matched to make them see the connection that equivalent fractions are equal in size, the equivalent fractions presented vary visually. This helped pupils to attempt multiple choice questions like the following:
This was also tested using equivalent improper fractions. In the image titled Part 9, I particularly like (c) and (e) because the parts are split horizontally and vertically. Engelmann here has varied the non-relevant aspects of each image: the number of units for each image, the shape being cut horizontally and vertically etc. What matter is the whether the area between each image is the same, if so then those fractions are equivalent. At this stage, pupils are not being asked to demonstrate equivalence using times tables between two fractions.
13. Multiplying fractions to demonstrate equivalence
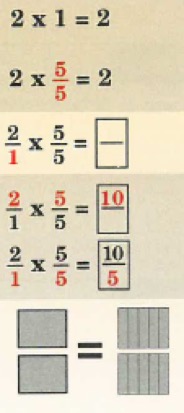 Pupils are taught that if you multiply an integer by a fraction which is equal to 1, then the result is the integer in the question. Images are provided to show that you are taking two whole units, and splitting the shape into more parts in each unit.
Pupils are taught that if you multiply an integer by a fraction which is equal to 1, then the result is the integer in the question. Images are provided to show that you are taking two whole units, and splitting the shape into more parts in each unit.
Pupils are also learning to spot visually that when you multiply an integer by a fraction with the same numerator and denominator that it is equivalent to multiplying the integer by one.
Pupils are taught how to structure their working when multiplying fractions where they write the integer with a denominator of one, then multiplying the numerators, and multiplying the denominators.
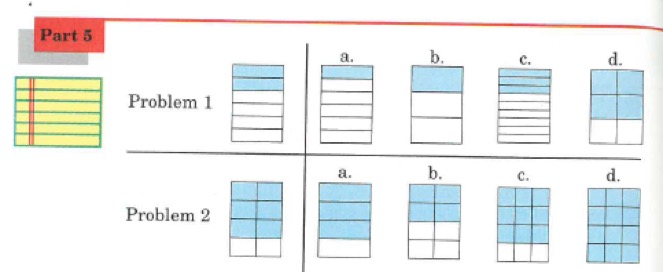
14. Placing fractions on a number line (work on)
This was an exercise that pupils did find difficult. Pupils had to place an improper fraction on the number line. What pupils found the most difficult was picking an integer equivalent fraction which two-fifths came after. For example:
I want to place two-fifths on the number line. I will go to the integer with a fraction which is just before two-fifths. I will go to zero-fifths, and count two parts to find two-fifths.
I want to place nineteen-fifths on the number line. I will go to the integer with a fraction which is just before nineteen-fifths. I will go to fifteen-fifths, and count four parts to find nineteen-fifths.
I want to place thirteen-fifths on the number line, I will go to the integer with a fraction which is just before thirteen-fifths. I will go to ten-fifths, and count three parts to find thirteen-fifths.
Exercises were included where pupils were asked to also label fractions onto a number line where the integers, or the integers’ equivalent fractions aren’t labelled.
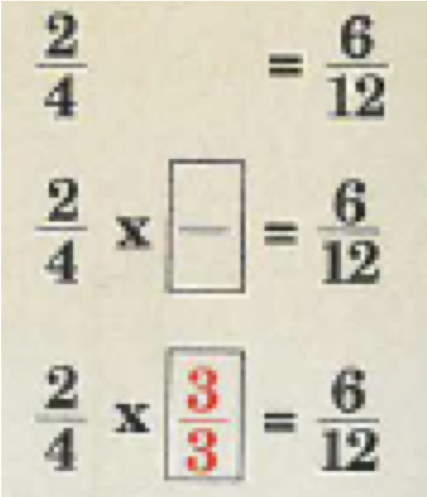
15. Equivalent Fractions – Multiplying a fraction by 1
In this exercises pupils are demonstrating equivalence between two fractions by writing the fraction to multiply the first fraction by to get the second fraction.
Pupils were using times tables to identify what the first fraction’s numerator and denominator are multiplied by. This fraction has the same value in the top and bottom of the fraction which then simplifies to one. Equivalent fractions are multiplied by a fraction which simplifies to one. This is also visually demonstrated.
Below is an example of an exercise, where pupils are asked to state the fraction for each image, and demonstrate equivalence by multiplying fractions.
A teaching point to mention: I did have to structure the working out for the pupils. I would say:
- I will write the first image’s fraction
- I will write a times sign
- I will draw a box for my missing fraction to show equivalence
- I will write an equal sign
- I will write the second image’s fraction
- What number goes in the top of the fraction?
- What number goes in the bottom of the fraction?
- Check that this fraction simplifies to one?
- Are these fractions equivalent? Yes or No?
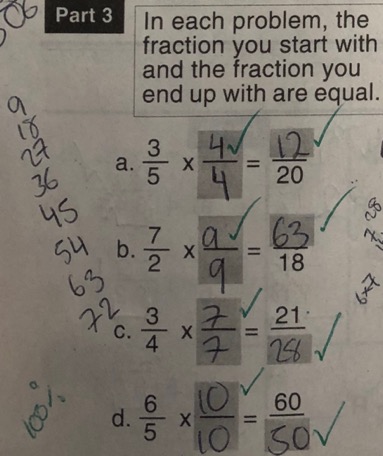 It was important to include this because I wanted pupils to know exactly how to demonstrate their working out. The pupils in this group struggled to structure their understanding on paper in way which made sense to somebody reading their work. By sticking to the following, essentially sticking to a ‘script’ then pupils were able to demonstrate equivalence consistently in this type of exercise throughout the book.
It was important to include this because I wanted pupils to know exactly how to demonstrate their working out. The pupils in this group struggled to structure their understanding on paper in way which made sense to somebody reading their work. By sticking to the following, essentially sticking to a ‘script’ then pupils were able to demonstrate equivalence consistently in this type of exercise throughout the book.
Pupils were then given exercises where one fraction was equal to an incomplete fraction where they filled in the blank and the fraction that they were multiplying by. Here is an example of a pupil’s work.
In my next blog post, I will outline the remaining fraction skills that are taught in Engelmann’s sequence of lessons.
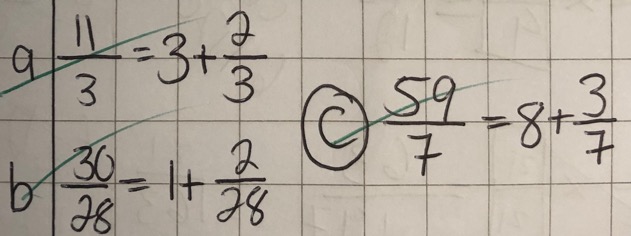
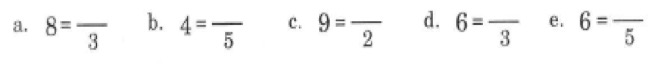




Leave a Reply
You must be logged in to post a comment.