Knowledge is important – particularly in maths. There are some concepts such as square numbers, where for example 2^2= 4 and 5^2= 25. Students are taught that 2 x 2 = 4 and 5 x 5 = 25. Through extensive repetition and practice, students are able to identify 2^2= 4 because they are no longer processing the calculation: instead they are retrieving this piece of knowledge from their long term memory. It should be an act of memory retrieval. Something I emphasised a lot I my previous blog.
Square numbers are an essential part of Pythagoras’ theorem, but without having any knowledge of Pythagoras’ theorem a student’s knowledge of square numbers is inflexible. Inflexible knowledge is “the unavoidable foundation of expertise, including that part of expertise that enables individuals to solve novel problems by applying existing knowledge to new situations.” (Willingham 2002:32)
I want to emphasise that inflexible knowledge is the foundation of learning. It is vital that we ensure our KS3 students build a bank of knowledge in their long term memory, even if that knowledge is inflexible, because as students start to accumulate knowledge over the years the connections and interplay between different pieces of knowledge allows for deeper learning to develop. This deeper learning in turn induces this bank of ostensibly inflexible knowledge to become flexible.
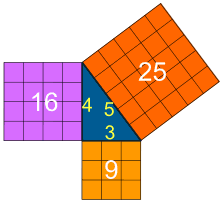
For example, square numbers should be drilled. Students should be able to recite 2^2= 4 and 5^2= 25 without thinking. They should not be processing that calculation; instead, they should retrieve it from long term memory. Now, squaring numbers can be extended to completing calculations such as 2^2 + 5^2 = 4 + 25 = 29. When introducing Pythagoras’ Theorem, students need to be taught that a^2 + b^2 = and that a and b refers to the two lengths which meet at a right angle of a right angled triangle: that the total of both squared lengths is the squared length of the hypotenuse.
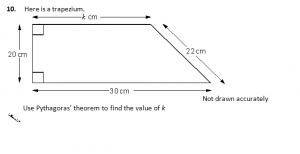
Until students take on board this information they cannot proceed with Pythagoras’ Theorem. Once students learn the formula, the application of square numbers evolves into new knowledge; this is flexible knowledge, where “It can be accessed out of the context in which it was learned and applied in new contexts.” (Willingham 2002:32) In KS4, students can start solving questions like this with more ease given that different pieces of knowledge now connect to become flexible:
Inflexible knowledge consists essentially of facts, e.g. square numbers, the formula to calculate the area of a circle, and quadratic formula. If given the time to be learnt to the point of memory retrieval, we empower our students to apply such inflexible knowledge to a deeper instruction, e.g. Pythagoras Theorem, the area of a sector, and finding the solution of a quadratic expression. Surely we desire our students to be experts?
If so, we must begin with teaching knowledge – facts – only then will our students become experts and only then will “their store of knowledge…become larger and increasingly flexible, although not immediately.”(Willingham 2002:49)
These increasingly large stores of facts and examples are an important stepping stone to mastery. (Willingham 2002:49)



Leave a Reply
You must be logged in to post a comment.