I remember marking books; I didn’t find it very useful. However, I found marking exit tickets incredibly informative because I was able to act on the assessment of pupils’ learning the very next day. Compare this to marking books every two weeks on work that I would be giving feedback to pupils who completed this work two weeks ago…and I am giving them feedback too late. Does anybody else see the elephant in the room?
I do think that marking books is a time consuming task which requires a great deal of input from teachers for a nominal amount of benefit for pupils. For this reason, we have a no marking policy at Michaela. What we do is mark our weekly quizzes. For each subject, let’s say pupils are given their maths homework on Friday, they will have a quiz on content that has been taught in the past week, and that has been given as homework on the following Monday. This is a whole school policy. It works in science, as I have observed as a teacher. Similarly, it works with all our other subjects. It is incredibly effective. It gives me an idea of how much pupils have learnt, and how much knowledge they have retained. More importantly, I can act on the feedback within my teaching in a timely fashion, and not two weeks later.
On several occasions, I have been asked how pupils are assessed at Michaela. This post will go into how we assess pupils using low stake weekly quizzes; we then have bi-annual assessments which measure how much pupils have learned and retained over a large period of time.
Every week, pupils are given a low-stake quiz testing how much of what has been taught in the week before it has been mastered and committed to memory. At Michaela, we believe that if it hasn’t been committed to memory then it hasn’t been learned. I cannot reiterate how much I believe in this, and indeed even more so after starting at Michaela from September 2015.
On Friday, pupils will be given their maths self quizzing homework. Joe Kirby goes into detail here about self quizzing in a previous post of his. Pupils will then have a quiz on Monday testing them on how much of their self-quizzing on maths definitions has been committed to memory, and whether the procedural calculations learned the week prior have been mastered.
Before I go into how the quiz is made it is really important to decide as a faculty what the purpose behind the assessment is. Is there any benefit in the quiz that I have made? What is the intention behind this low stake quiz? Our low-stake quizzes are testing whether pupils have committed the knowledge from their self quizzing to memory, and whether the procedural calculations have been mastered. Knowing such a purpose, this guides the structure and content of the quiz.
Each quiz has 8 – 12 questions testing pupils on procedures that have been taught in the previous week. We do not test pupils on content that has not been taught. I repeat, we do not test pupils on content that has not been taught. Why? This is because we are testing whether pupils have mastered the content that has been taught, and that means that the sample of knowledge that is being tested is small, rather than large.
Quiz 1:
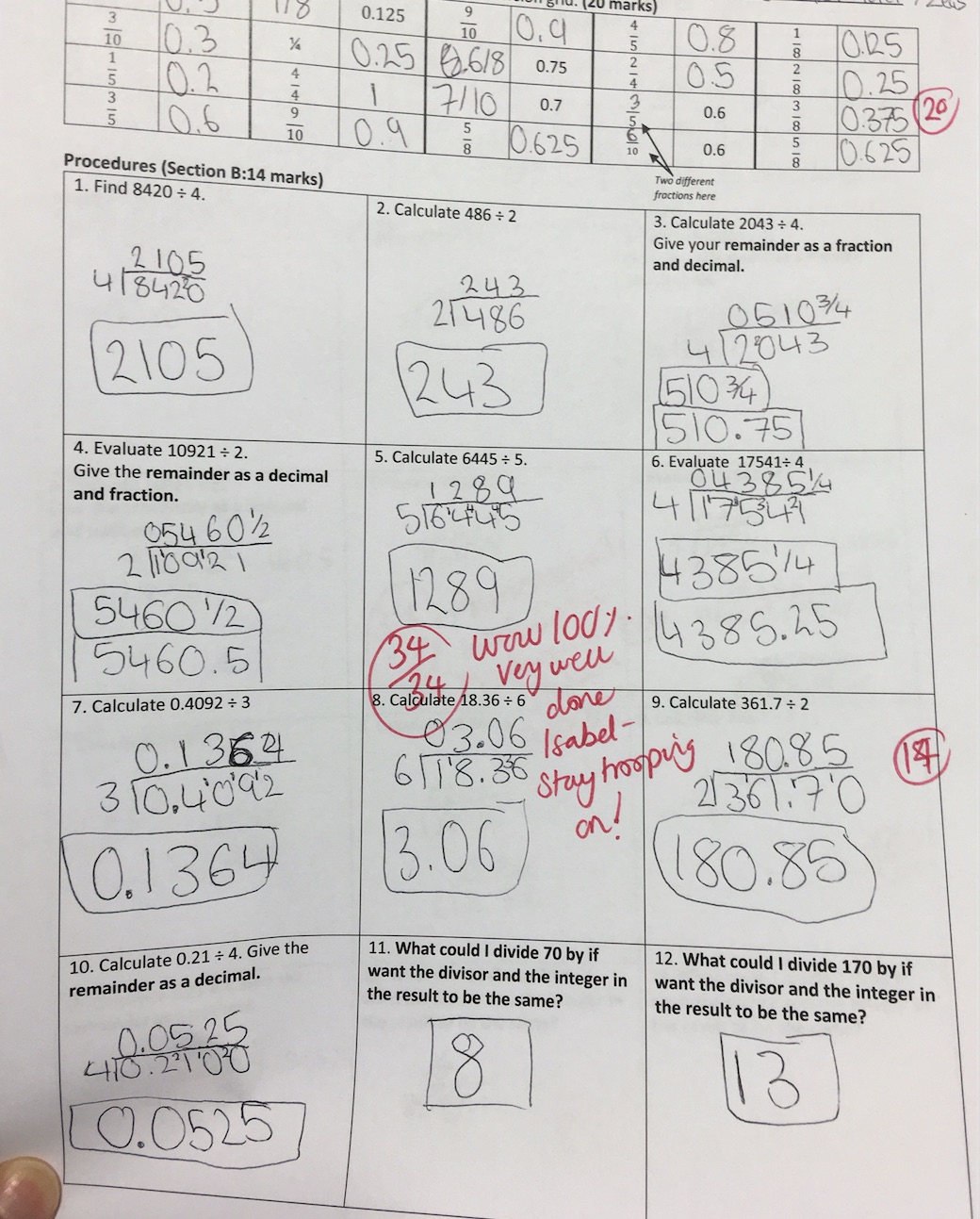
Here is a year 7 quiz testing pupils on their week’s worth of teaching on short division. Each question selected is testing pupils on a specific skill:
1) Short division where there is no remainder – but with one digit where it is smaller than the divisor. For example, when dividing 8420 by 4, 2 is too small therefore the digit will be 0, and then carry the 2 as the remainder to the next digit to become 20.
2) Short division where there are no remainders, and each digit in the dividend is greater than the divisor.
3) and
4) The first digit in the dividend is smaller than the divisor. Also, stating the remainder as a fraction, where the remainder is the numerator and the divisor is the denominator. Also writing the answer where the remainder is a fraction and a decimal.
5) Short division where there are remainders that need to be carried to the next digit. The answer is perfectly divisible by the divisor.
6) Short division where there are remainders that need to be carried to the next digit. The answer has a remainder which needs to be displayed as a fraction as well as a decimal.
7) Short division of a decimal (less than 1) where there is no remainder
8) Short division of a decimal (integer and decimal) where there is no remainder
9) Short division of a decimal where pupils must write their answer in decimal format. They have to put additional zeros to continue the decimal to allow the remainder to be carried.
10) Short division of a decimal where pupils have to put several zeros to continue the decimal to complete the division.
11) Question where pupils have to identify the closest square number to the dividend and identify that the divisor and the integer as a result will be the same.
Quiz 2:
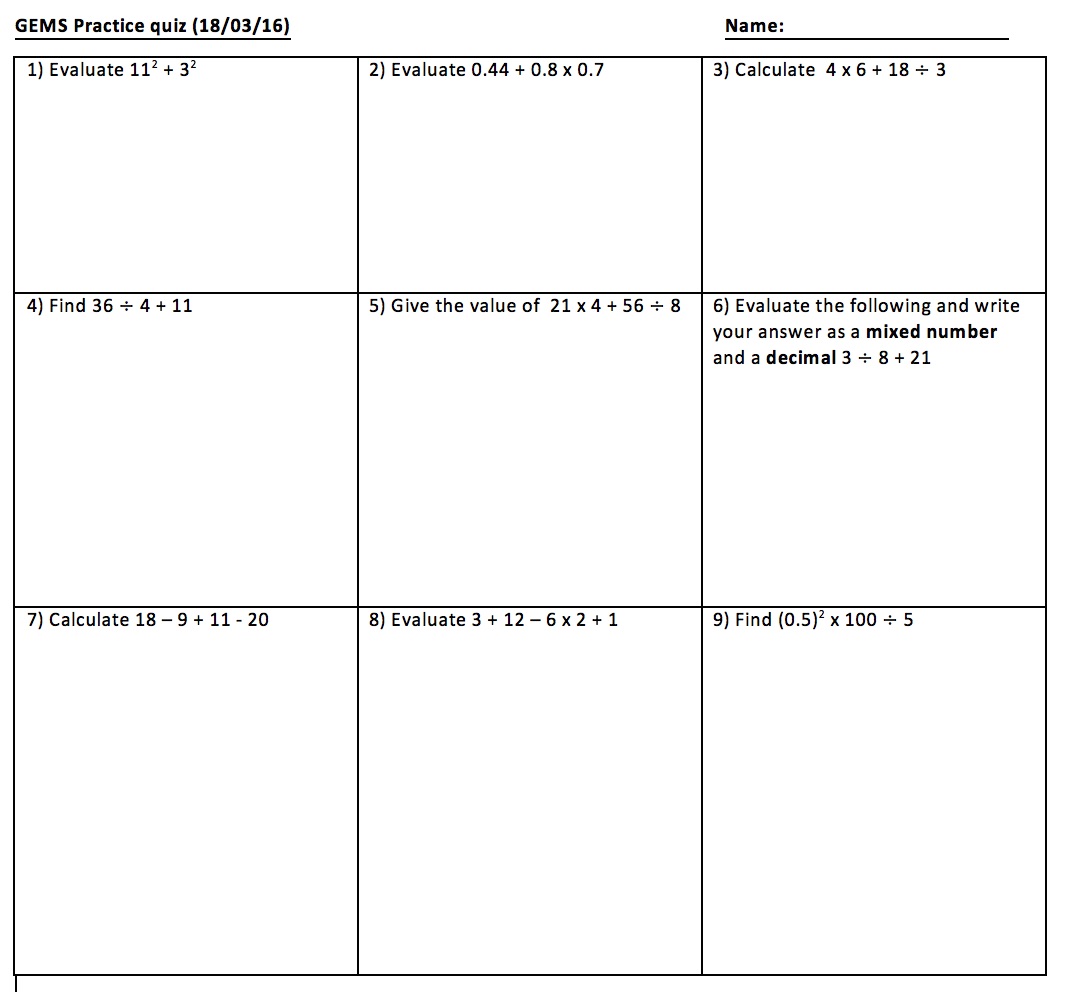
Here is a year 7 quiz testing pupils on their week’s worth of teaching on GEMS (Groups, Exponents, Multiplication (and division) and Subtraction (and addition). We teach GEMS as opposed to BIDMAS or BODMAS. Each question selected is testing pupils on a specific skill:
1) evaluate exponents before addition (GEMS)
2) multiplication comes before addition where addition is visually first in the question (GEMS)
3) two groups of multiplication and division where they come before addition. Must identify both and then add. (GEMS)
4) multiplication comes before addition where division is visually first in the question (GEMS)
5) Another group similar to Q3 – additional but not necessary
6) Multiplication comes before addition but can they identify that the division will result in a fraction which can be added to 21. (GEMS)
7) Practise left to right when we only have addition and subtraction operations because they are equal in GEMS.
8) More complex GEMS question because of a mixture of operations (GEMS)
9) Can pupils identify whether they can apply GEMS correctly where we have exponents, and then go left to right because of multiplication and division being equal in GEMS.
Quiz 3:
Here is a year 8 quiz testing pupils on their week’s worth of teaching on the topics: formulae, rearranging equations to change the subject of an equation.
Q1 + 2) Mastery on deciphering whether the length given is the radius/diameter, and identifying whether we must substitute into the formulae for area or circumference, and whether they can recall the correct formulae for either concept.
3) Calculate the area of a trapezium given the slant height and perpendicular height. Shape is also orientated. Can they distinguish which is which, and which length must be substituted into the formulae? Furthermore, can they recall the formulae memorised?
4) Mastery of understanding how to substitute into the formula for the volume of a cone, and recall the formula too. Deliberately radius is given to ensure that pupils are being tested on whether they can correctly substitute into the formula.
5) Substituting into the equation M = DxV but must identify that the volume is not given. Can they calculate the volume of a cube first, and then find the mass?
6) Substituting into the equation D = SxT but must identify that time is given in minutes and must be converted into hours. Also, that the speed is given in kilometres instead of miles.
7) Calculate the volume of half a sphere given the radius. Can pupils identify that they must half the result after using the formula or use the formula 4/6pi(r) ^3 or 2/3pi(r)3?
8) Rearrange the subject of the equation where we must expand the brackets. Implied in the question by stating “simplify your answer fully” hoping to see the result b2 + 32b + 256.
9) Rearrange the subject where the unknown is the denominator.
10) Rearrange the subject for basic one step rearrangements besides the last one where the unknown is negative. Can pupils spot that the we must multiply or divide both sides by -1 to get m as the subject of the equation.
The quizzes are testing whether pupils have mastered the procedural questions. To make questions challenging we have given the diameter instead of the radius when calculating the area. We have orientated the trapezium, and given both the perpendicular and slant height. We have made it more challenging because we are testing mastery. The rigour in the assessment allows for the rigour in the teaching, and pupils do indeed perform. We spend a significant amount of time at Michaela talking about how the only score to celebrate is 100%. I write postcards for the pupils that get 100% in their quizzes and make a huge deal out of it. Pupils love the feeling of success, and appreciate the admiration from their teachers who recognise the success in scoring 100%.
Low stake quizzes are incredibly powerful because they inform your teaching and planning. If lots of pupils have made a mistake on the same question, this informs me that either they have all missed the point, that I have to reevaluate how I teach the concept in the first place, or both of these points. I hope you find this useful.

Leave a Reply
You must be logged in to post a comment.