Conception of the good

On Saturday, I delivered a workshop which looked at seven specific high-leverage procedures that should be automatised for pupils to successfully learn certain concepts taught in AS Mathematics. The purpose was to raise awareness of the amount of procedural fluency required for different sub-procedures in large calculations such as when completing the square, or simplifying index notation etc

Here is a bit of context behind what inspired me to deliver this workshop. I was tutoring a friend’s daughter in the summer holidays (2016) before she started learning AS Mathematics after achieving a A in her maths GCSE. My friend’s daughter is intelligent, enjoys studying mathematics and is able to learn new concepts very quickly but she struggled to make the correct decisions to complete each sub-procedure in long calculations. She would struggle to multiply an integer and a fraction, because she didn’t know what decision to make i.e. write the integer as a fraction over one.  So I spent a lot of time creating questions within drills and deliberate practice exercises for her to gain the procedural knowledge to a degree of fluency where she wasn’t struggling to complete different sub-procedures.

I am going to look at one high level procedures that I mentioned in my workshop; multiplying fractions.

Multiplying fractions.

Historically, when teaching how to multiply fractions we teach how to multiply fractions where there are two terms within the equation. However, there are several different problem types that can be taught:

• Multiplying two terms
• Multiplying more than two terms
• Multiplying terms that share factors that can be cross-simplified
• Multiplying a fraction and an integer
• Multiplying a mixed number and a fraction
• Multiplying mixed numbers
• Multiplying decimals (that can be converted into fractions) and fractions.
• Multiplying an improper fraction with and/or proper fraction

When teaching my tutee index notation she struggled to attempt the following problem because she wasn’t able to identify how to multiply an integer with a fraction. I told her explicitly how to multiply 2 and a third quickly, because that is what I do, and all pupils do this if and when they spot the pattern (but not applicable when the numerator of the fraction is not 1).

Later on in another session, my tutee struggled with the following question because she didn’t realise that a fraction can be written as the product of an integer (numerator of the fraction – 2) and a fraction (unit fraction with the same denominator – 1/3 ) e.g. 2/3 equals to the product of 2 and 1/3.

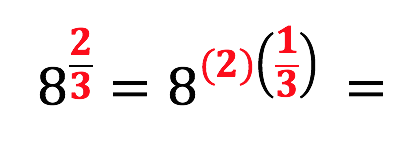Furthermore, this piece of procedural knowledge is necessary to attempt the following question:

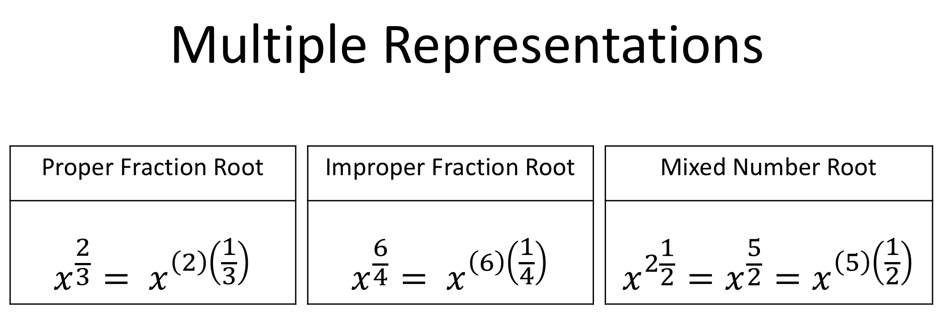
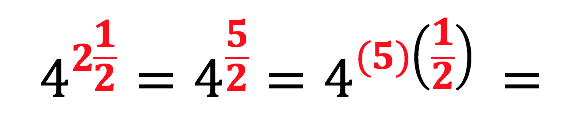And again, when a question gets more complex like the one below because the base number is a mixed number, rewriting 5/2 as a product of 5 and ½ is a necessary step to evaluate the question.

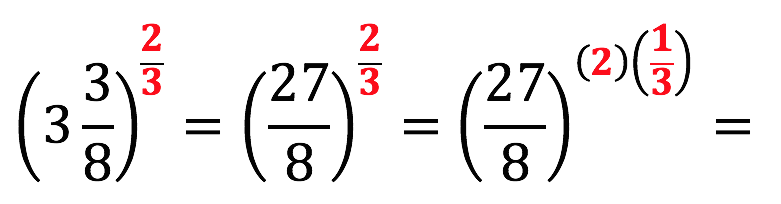However, what the take-away here is is that multiplying fractions is a high leverage procedure. A part of the procedure is to rewrite a fraction as a product of an integer and a fractions. So how can pupils learn this  to successfully automatise their procedural knowledge of multiplying fractions? This can be achieved through an understanding of multiple representations of the following possible problem types that arise when evaluating the base number/term held to a power which is a fraction.

The emphasis of exploring different problem types available within the topic of multiplying fractions, and recognising that a fraction is a product of an integer (numerator of the fraction) and a fraction (unit fraction using the same denominator), and then seeing the multiple representations of this enables a level of proficiency to allow successful learning of new content. My tutee wasn’t really learning how to simplify indices because she was focusing on learning how to complete each sub-procedure. I think this proficiency needs to be achieved in KS3.

In my next post, I shall give another example – halving!