In my last post, I discussed whether an instructional programme could be created to teach a deeper concept of mean. I mentioned five different properties.
After a conversation with Kris Boulton about the blog post, he spotted something interesting about property 5.
Property 5: The average is only influenced by values other than the average.
At the end of my previous post, I explained property 5. It is because when we add the average value to the data set then the resulting sum is divisible by the mean. When we add a value that is not the previous average, the resulting sum is not divisible by the new denominator. However, the second sentence is incorrect.
If I do not add the average value of the original data set, I can still have a resulting sum which is divisible by the new denominator. The third example shows this.
Example 1: Original data set with a mean of 5.
Example 2: Add the average value to the new data set – resulting sum is divisible by the new denominator. The mean has not changed.
Example 3: Not adding the average value to the new data set – resulting sum is still divisible by the new denominator. The mean has changed.
Is there another way to communicate this property?
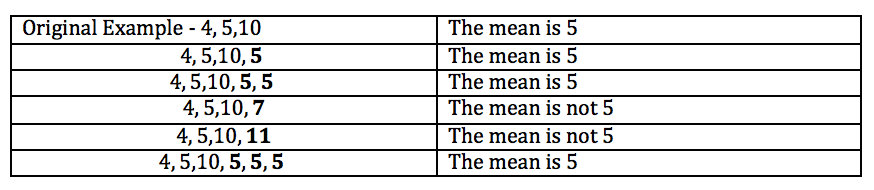
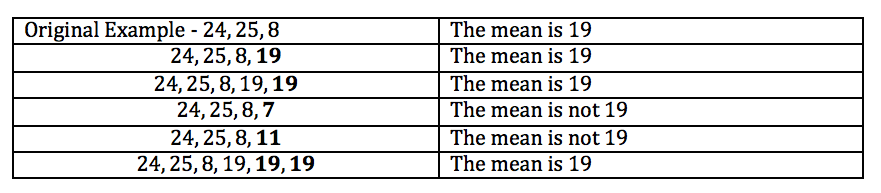
This is an idea from Kris which he discussed as a potential second attempt to communicate property 5. It communicates property 5 nicely. It also has non examples too. If I do not add the average value then the mean is not 5. Below is another example that can go along with the example above because the average value (19) is not a number in the original data set. Pupils are then seeing an example where the average value can be present in the data set, and where the average value will not be a number in the data set.
I have added the average value to the original data set.
The mean has not changed.
I added the average value twice to the original data set.
The mean has not changed.
I have not added the average value to the original data set.
The mean has changed.
I think both examples are important to use because they communicate the same property. The second example communicates the message in a more explicit fashion. The first example should be included because it is a nuanced example compared to the second. This may or may not be that important, but telling a pupil that the average value can be a number in the original data set is knowledge a pupil should know.
I wanted to convey an example where the procedure of dividing by the number of values was visible to pupils. However, at the same time, what is the most important aspect is pupils seeing that we have added the average value and the new average hasn’t changed. The division isn’t adding the value that I initially thought it was. The new examples communicate a quality of sameness that can clearly communicate the property effectively. Also, showing the features of the new data set which are permissible to be a positive example, and the non examples show the features of the data set which are not present to be an example for property 5.
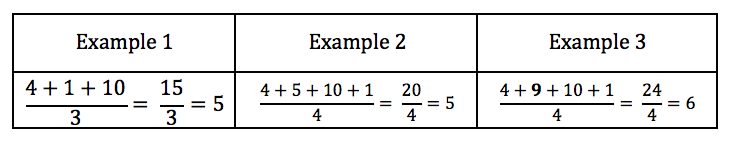
Leave a Reply
You must be logged in to post a comment.