In my last post I outlined how I developed pupils’ knowledge of rational numbers and simplifying surds in preparation for pupils to solve the following equations.
I asked them if we could have any number that could be squared to result in a negative number. This was the point in the session that I introduced the idea of imaginary numbers. I gave them a brief history referring to the work and discussions by Rene Descartes and Leonard Euler.
Now, “If I can square a number to get a negative result then it is an imaginary number because when we square a positive number we get a positive result, and when we square a negative number we get a positive number. This is how we display the square of an imaginary number”:
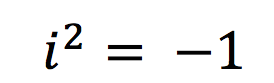
I told the kids that this is a fact that we are going to accept. Now let’s move on. “We are now going to square root both sides to see what is equal to. We can’t square root a negative number but I am going to present it like this, and we can present it like this, again we are going to accept this for now and move on.”

These two knowledge facts are the foundation in solving the next few problems which I reiterated again and again to the kids. I then showed how we can evaluate the two calculations shown at the start where the square of an imaginary number will result in a negative integer answer. I explicitly outlined each step, one by one, and I kept each line of the algorithm between the equation and the solution consistent for each question I demonstrated.
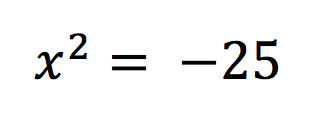
“I am going to square root both sides, and I am going to include the positive and negative sign in front of the square root. We must include this.”
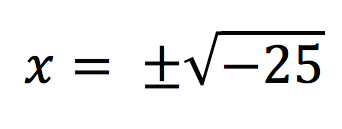
“I am going to separate √-25 as a calculation of √25 and √-1 because I can then square root positive 25.”

“I am going to evaluate √25.”
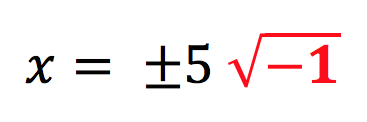
“How handy! I know that √-1 is equal to . We are using our knowledge facts which I showed you midway into our session,”
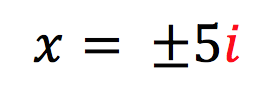
“This is my final answer.”
I demonstrated another example, and then asked pupils to attempt a selection of questions by themselves.
I then told the pupils, “We are now reaching the peak of our lesson where we are going to combine our knowledge of finding the solutions of a negative number, but this time the number that is going to be square rooted will not be a square number, this is where our knowledge of simplifying √24 and √500 will help us here.”
I modelled the next example with the following teacher instruction:
Here is my problem:
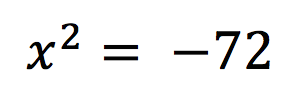
“I am going to square root both sides, include the positive and negative sign in front of the square root, -72 will be within the square root”
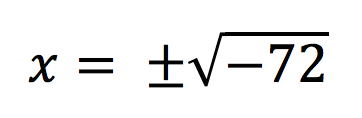
“I am going to separate -72 where it is shown as a product of -1 and 72, both values will be within a square root.”
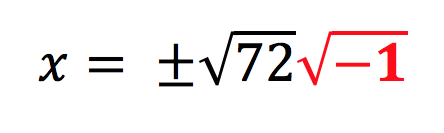
“I am going to simplify the square root of 72 where I have an integer and a non rational number, because the square root of 72 is positive, no longer negative!”
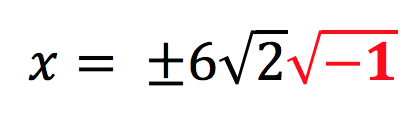
“I am going to replace the square root of -1 with .

“I am going to rewrite this so i is next to the integer, you will do the same for all your answers too. We are finished.”
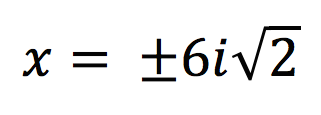
This is an example of a session that was delivered where the goal at the end was to have pupils being able to solve equations where they had to combine their understanding of rational numbers, and imaginary numbers. Pupils who attend this session are learning about different concepts in a succinct and limited manner to then apply their understanding to specific problem types selected by myself and the department. The questions the kids did to apply their understanding were carefully crafted by me to ensure that pupils were deliberately practising what I had modelled on the board. I think it worked quite well. If anything It made me realise that through a strong foundational understanding of number and times tables and thought out instruction, we can teach something as abstract as imaginary numbers. Furthermore, to get the delivery of the worked example to be as tight and accurate as possible I did script this lesson and rehearse it as well.
The idea of imaginary numbers is huge! There is so much that can be taught but I narrowed the focus to ensure that pupils could achieve the goal required. I have attached a few images of pupils’ work, and a video of a pupil dictating his understanding to me. I stop him because he did not simplify the surd where we had the greatest possible k integer. The pupil was correct in the method that he was using as it had two steps, but I wanted pupils to simplify the surd using the largest factor.
This post explained how I taught pupils the procedure of solving equations where the result has an imaginary number. The video posted shows the outcome of the session where two pupils solve one equation. Enjoy the video available at this link with a selection of photos of the pupils’ work.
https://1drv.ms/f/s!AjSSrbwXqTsRhFjuw0ViPISNYBns
Think this sounds interesting? Come visit! We love having guests. It challenges our thinking and it boosts the pupils’ confidence to have people come in to see them.
Think it sounds wonderful? Apply to join our team of enthusiastic maths nerds! We are advertising for a maths teacher, starting in September (or earlier, for the right candidate). Closing SOON: https://www.tes.com/jobs/vacancy/maths-teacher-brent-440947
Leave a Reply
You must be logged in to post a comment.