Conception of the good

Last summer, I made as many different problem types for the topic of Circle Theorems. I looked through different textbooks and online resources (MEP, TES, past papers). I did this because when I last taught circle theorems at my previous school there weren’t enough questions for my pupils to get sufficient deliberate practice. This was a two fold issue. Firstly, I would find a practice set of questions which would not provide enough questions for a pupil to practise one particular problem type. Secondly, the sequencing of questions in terms of difficulty would escalate too quickly or not at all. Here I will outline the different problems types I created (using activeinspire) and then explain the thinking behind them. I have been very selective with the problems I have included here; I have made more questions where certain problems types are more complicated which I shall discuss at the end. I shall more in the following posts.

I made two different categories of problems for each circle theorem. The first type would explicitly test a pupil’s understanding of the theorem to see if they could identify the circle theorem being tested.

The second type would be testing two things. Firstly, such a problem type would be testing their ability to determine the circle theorem being applied in the question. The second aspect of the problem type would be testing related geometry knowledge interleaved which can be calculated as the secondary or primary procedure in the problem e.g. finding the exterior angle of the Isosceles triangle.

One common theme in these questions is that procedural knowledge applied is executed in a predetermined linear sequence. Hiebert and Lefevre wrote that “the only relational requirement for a procedure to run is that prescription n must know that it comes after prescription n-1.” Multi-step problems such as the ones that you will see show that procedures are hierarchically arranged so that the order of the sub procedures is relevant. Here are the different problem types for each circle theorem where I explain how many items of knowledge is being tested in each question, and what each item of knowledge is.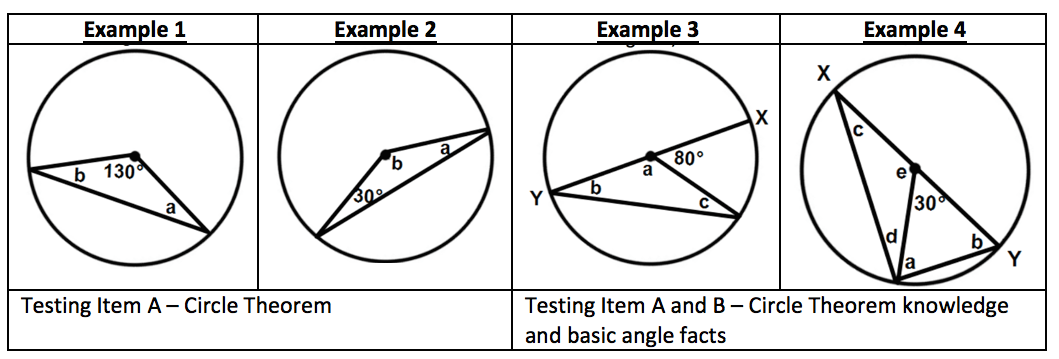Figure 1: A triangle made by radii form an Isosceles triangle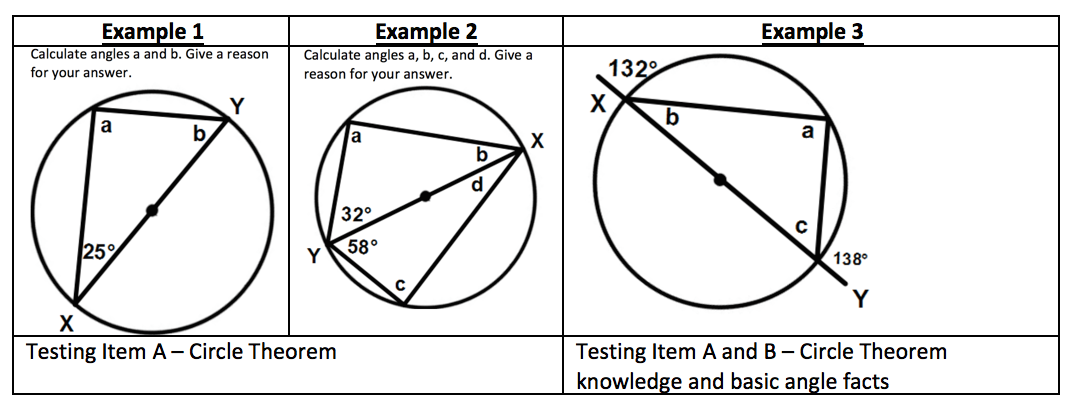

Figure 2: The angle in a semi-circle is a right angle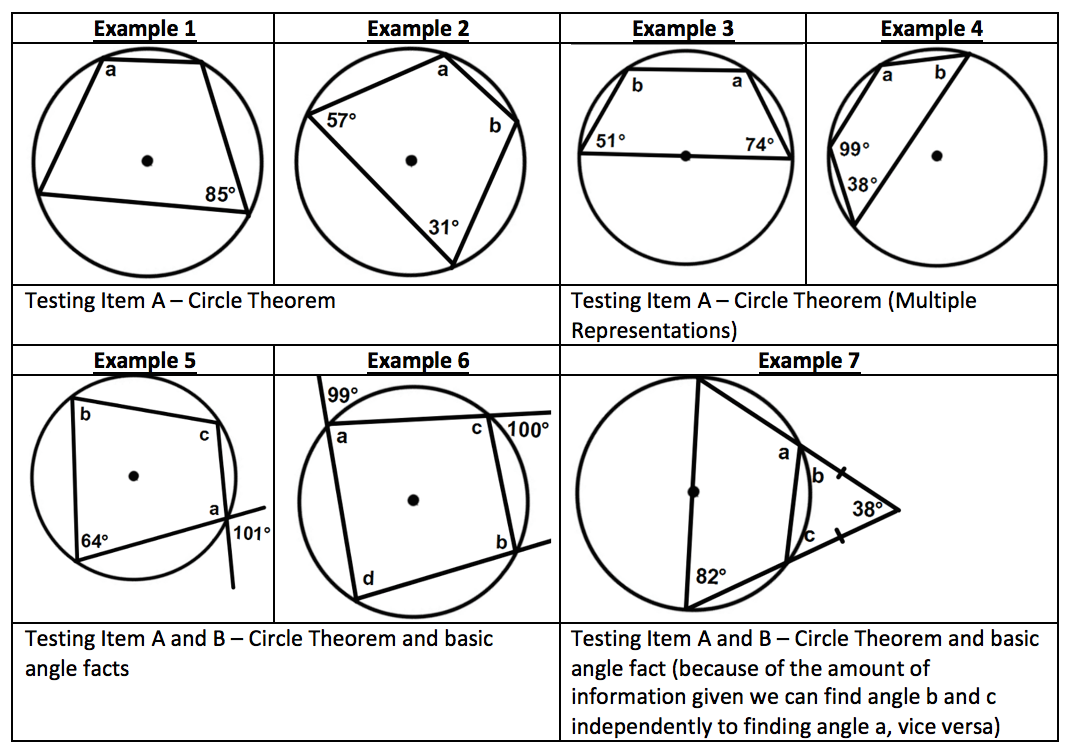

Figure 3: The opposite angles in a cyclic quadrilateral add up to 180 degrees (the angles are supplementary)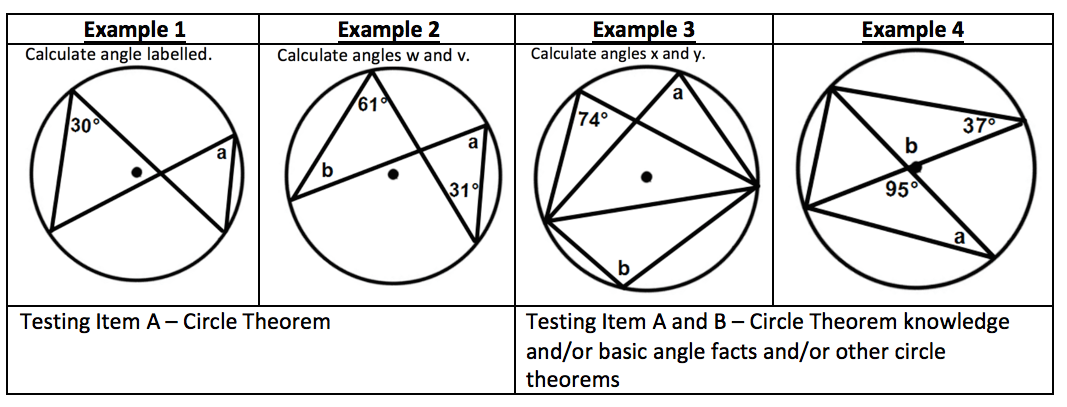Figure 4: Angles subtended by an arc in the same segment of a circle are equal

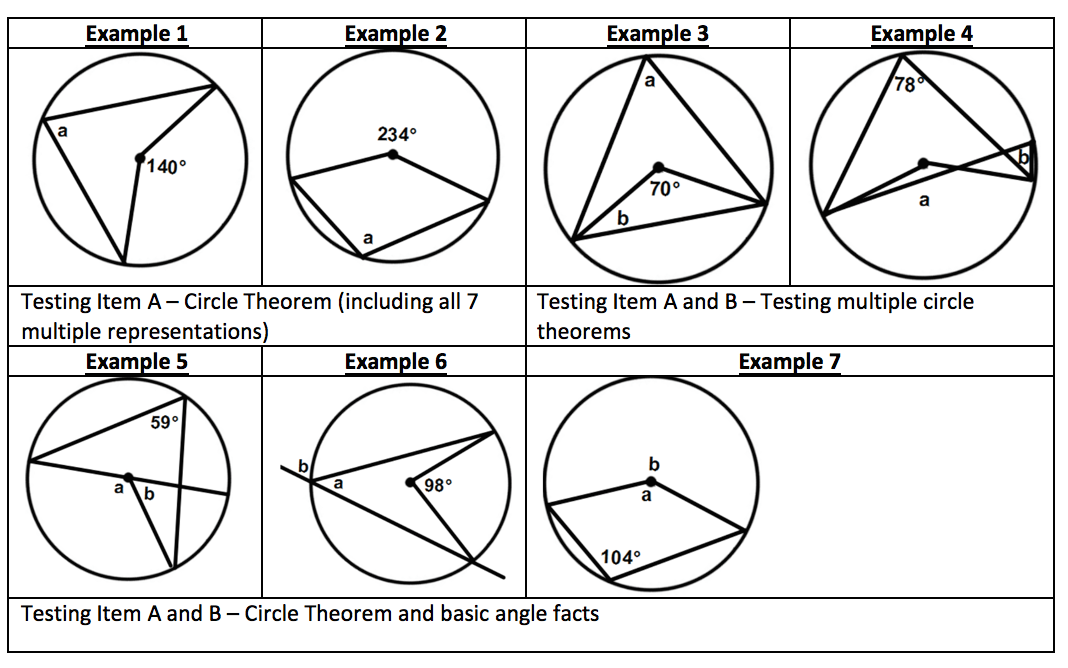
Figure 5: The angle subtended at the centre of a circle is twice the angle subtended at the circumferenceFigure 6: Tangents to circles – From any point outside a circle just two tangents to the circle can be drawn and they are of equal length (Two tangent theorem)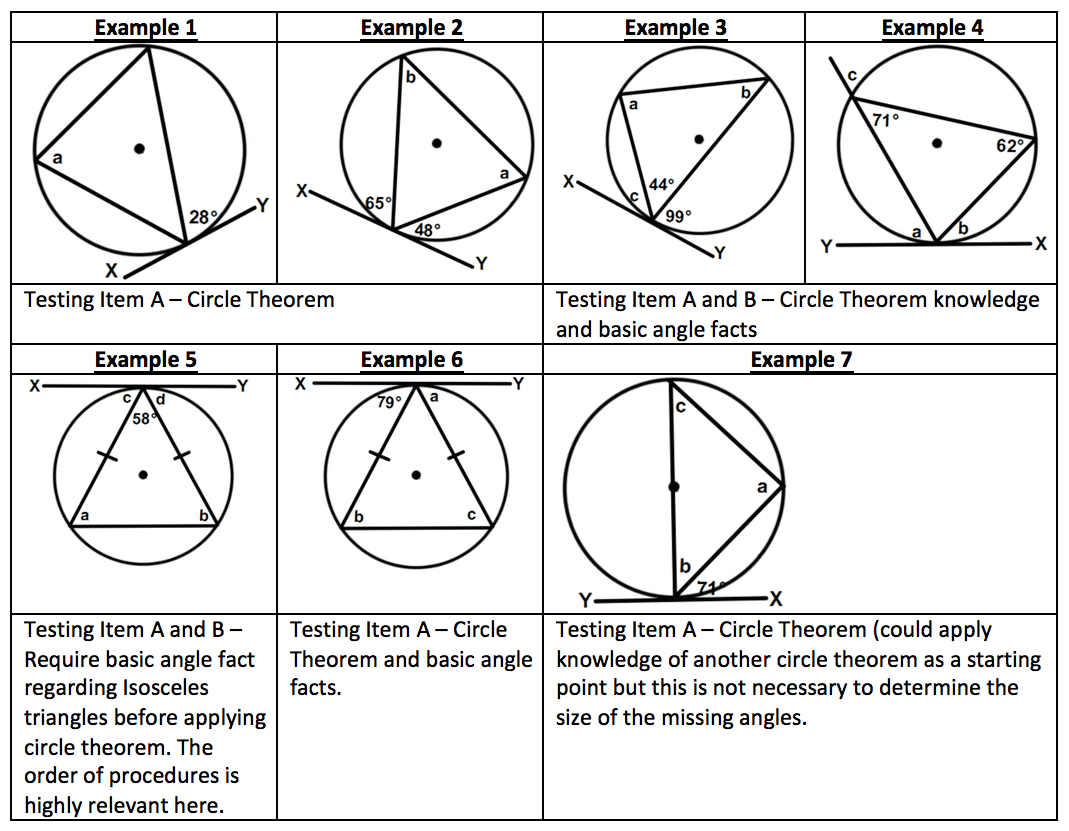Figure 7: Alternate Segment Theorem – The angle between a tangent and a chord through the point of contact is equal to the angle subtended by the chord in the alternate segment.

To conclude, there are many different problems types for the topic of circle theorems and the complexity of the problem can be addressed in many ways such as:

• arithmetic complexity
• Orientation of the problem
• Multiple representations of the same problem type
• multiple subprocedures to determine multiple missing angles
• Interleaving the application of multiple circle theorems.
• Interleaving the use of basic angles facts
  1. as a necessary step in the procedure to find other angles
  2. as an independent step in the procedure where finding one angle is not necessary to find another angle.

I would be keen to hear any thoughts. Please don’t hesitate to email me on naveenfrizvi@hotmail.co.uk.