Today’s blog post outlines how I have broken down the teaching and planning of the initial (first-time) teaching of fractions to bottom set Y7. Last summer, my faculty and I worked on tailoring our own Mathematics Mastery Scheme of work for the upcoming cohort of year 7 pupils.
The teaching and planning of our year 7 curriculum is part of a five year plan to ensure that, as teachers, we are preparing our KS3 students with essential knowledge; that through extensive retrieval quizzes, interleaving and distributed practice of core concepts our pupils will be able to problem solve and think critically in KS4.
However, there are a few key points about critical thinking that must be brought to the forefront of this blog:
1) to think critically depends on having adequate content knowledge;
2) you can’t think critically about topics you know little about nor solve problems not understood well enough to recognise and execute the type of solutions they call for; and
3) when one is very familiar with a problem’s deep structure, the knowledge of how to solve it transfers well.
Essentially, I am trying to emphasise that content and factual knowledge are the bedrock of learning. I am going to demonstrate how I have taught a selection of lessons on the topic of fractions, where I fragmented different pieces of inflexible knowledge, linking them to what can be referred to as a knowledge framework. Kris Boulton clearly explained the idea of knowledge frameworks in his most recent blog – of which I highly recommend reading.
A Knowledge framework “is a web of connected knowledge.”
I taught each concept below as fragmented pieces of inflexible knowledge to slowly transition students to interlink each concept taught, in turn forming a bigger picture. Eventually they saw the connection between each idea. How does halving by partitioning link to the concept of halving by dividing by 2? How can we take our understanding that halving entails the splitting of an amount into two equal sized groups to calculating a quarter of 44? How can we calculate a quarter of 44 using our basic times table propositions?
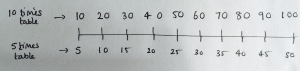
I spent a significant amount of time ensuring that my students were able to identify that of half of all the multiples of 10, and that this was committed to memory; initially, teaching them the half value for each multiple of 10 to 100 using a double number line, as previously demonstrated by David Thomas at the La Salle Education Conference in March.
Figure 1 – Double number line
Students were taught the link between 40 and its half value. We repeatedly practised this on mini-whiteboards throughout revision and testing. This was continuously practised for 2 – 3 lessons, followed by testing of this continuing less and less throughout the teaching of the unit. Here, students could successfully recall basic facts, e.g. that half of 70 is 35.
We moved onto calculating a half of 76 through partitioning (figure 1). Students were then halving two to three digit numbers by halving via partitioning (figure 2). Again, repetition was intense and then spaced out, with each test taking less time: students were now recalling factual knowledge; that the half of 70 is 35, in 3 – 5 seconds, but they were now also procedurally calculating the half of 76.
Figure 2 (left) – Student’s work on halving two digit even numbers via partitioning.
Figure 3 (right) – Student’s work on halving three digit even number via partitioning
As regular and spaced testing continued, students were starting to recall from memory that the half of 76 is 38; whereas the half of 46 is 23. If asked to explain, they could provide an accurate explanation, by demonstrating by portioning the two digit number.
Even though students were confident to half two and three digit numbers (specifically even numbers and not odd as of yet) I wanted to build upon their understanding of halving but in a different context. It went as follows:
Figure 4 (left) – Student’s work on multiplying fractions to determine a half of an even number
Figure 5 (right) – Student’s work on multiplying fractions to determine a half of an even number with division to go alongside
My rationale behind this was that it is absolutely irrelevant for students to explain to me right now why when we multiply fractions we multiply the numerator of both fractions to find the numerator of the result, and we multiply the denominator of both fractions to find the denominator of the result. What was valuable was that of students identifying that the result of 76/2 is equivalent to the familiar representation of 76 divided by 2 to achieve the result of 36. My students squealed with amazement – where the author does not exaggerate. They were dazzled that they could calculate half of 76 by partitioning; through the multiplication of fractions, as well as by dividing 76 by 2.
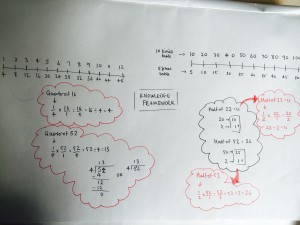
Here, I linked three fragmented and yet exactly the same pieces of factual knowledge in different contexts, where in terms of the procedures students followed them all to determine half of 76. As three separate pieces of knowledge, they were inflexible because independently no student has completely mastered the concept of halving. Now, through building a knowledge framework where students have linked the three different representations of the same concept, their knowledge and understanding of halving has become flexible: it can now be accessed out of the context in which it was learned importantly it can now subsequently be applied to new contexts.
Figure 6 – An example of a knowledge framework used during planning.
After a selection of worked examples, students with their sheer enthusiasm and revelation powered through a carefully designed exercise of questions. I then ran through the concept of calculating a quarter of 76, and the students were recognised as benefiting from the following:
Figure 7 (left) – Student’s work on calculating a half or a quarter of a number (all multiples of 4 when calculating a quarter)
Figure 8 and 9 (middle and right) – Student’s work on calculating a quarter of multiples of 4 using long division as well as multiplying fraction.
1) Students have a clearer and wider understanding of halving through building upon their factual knowledge of halving but in different representations. As a result this will aid students’ memory retrieval when they come across the same or similar problem types;
2) Students are now seeing the multiplication of fractions in a context which will not be so separate and fragmented in year 8 or year 9, because they have been introduced to it in a different capacity in year 7 – different but relevant.
3) The connection and interplay between the different representations of the same factual knowledge of halving enables students to see new ways of thinking, inducing deployment of the right type of thinking at the right time. This is what we need to achieve as teachers in order to teach our students to think critically.
It is truly a combination of building a solid bank of content knowledge through distributive, spaced and tested practice, and by showing the connections of the different representations of the same piece of knowledge. These separate representations are inflexible singly but together create a fluidity that enables critical thinking.
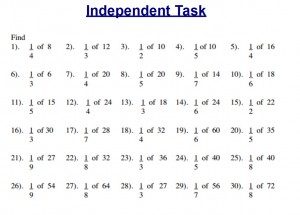
Today, students smoothly could solve the following questions with only two worked examples being demonstrated to them by me. Their knowledge has become flexible and fluid. It is amazing!
Figure 10 (left) – Independent Task completed by students
Figure 11 (right) – Student’s work on finding a fraction of an amount
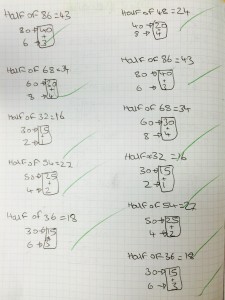







Leave a Reply
You must be logged in to post a comment.